Statistics Assignment: Probability, Z-scores, and Confidence Intervals

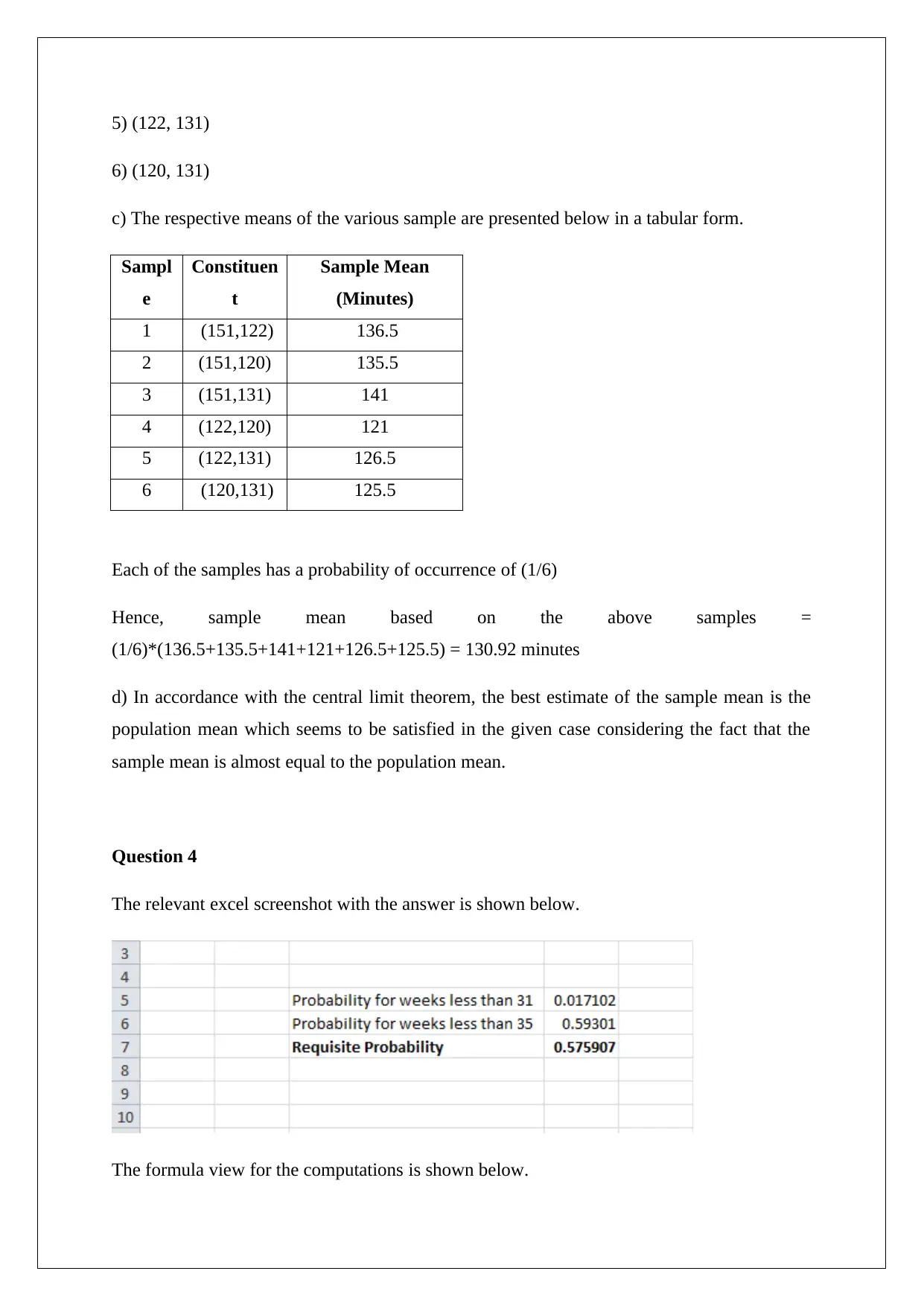
This document presents a comprehensive solution to a practical statistics assignment. The assignment covers a range of statistical concepts, including Z-score calculations, probability distributions, and confidence intervals. Question 1 involves calculating probabilities related to human pregnancy durations using Z-scores. Question 2 focuses on calculating probabilities associated with drive-thru times, again utilizing Z-scores. Question 3 delves into sampling distributions and the central limit theorem. Question 4 provides an Excel-based solution for standard deviation calculations. Question 5 analyzes weight data, computing probabilities of overloading based on the central limit theorem. Finally, Question 6 addresses confidence intervals, validating a reported value within a calculated 95% confidence interval. The solutions demonstrate a solid understanding of statistical principles and their application to real-world scenarios.

PRACTICAL STATISTICS
STUDENT ID:
[Pick the date]

Question 1
a) The requisite z value is 0.8750.
b) The area 0.1908 can be interpreted as the probability of the length of human pregnancy
exceeding 280 days.
c) The z value for top 10% is 1.28
Hence, the minimum pregnancy time = Z*standard deviation + Mean = 1.28*16 + 266 =
286.48 days
d) The z value for bottom 5% is -1.645
Hence, the maximum pregnancy time = Z*standard deviation + Mean = -1.645*16 + 266 =
239.68 days
Question 2
It is known that μ = 138.5 seconds and σ = 29 seconds
a) We use the following formula
Z = (X-μ)/ σ
Here X= 100
Z = (100-138.5)/29 = -1.3276
P(Z<-1.3276) = 0.092
b) We use the following formula
Z = (X-μ)/ σ
Here X= 160
Z = (160-138.5)/29 = 0.7414
P(Z>0.7414) = 1- P(Z≤0.7414) = 1- 0.7708 = 0.2292

c) Here X1 = 120 seconds
Z1 = (120-138.5)/29 = -0.6379
P(Z<Z1) = 0.2618
Also, X2 = 180 seconds
Z2 = (180-138.5)/29 = 1.43
P(Z<Z1) = 0.9238
Hence, P (Z1<Z<Z2) = 0.9238-0.2618 = 0.6620
d) Here X = 300 seconds
Z = (180-138.5)/29 = 1.43
P(Z<1.43) = 0.9238
Hence, P(Z>5.569) = 1-0.9238 = 0.0762
Thus, it can be concluded that it would not be unusual for a car to spend in excess of 3
minutes in the drive thru as the underlying probability exceeds 0.05.
Question 3
a) Population mean (μ) = (151+122+120+131)/4 = 131 minutes
b) The possible samples with 2 samples are as follows.
1) (151,122)
2) (151,120)
3) (151, 131)
4) (122, 120)

5) (122, 131)
6) (120, 131)
c) The respective means of the various sample are presented below in a tabular form.
Sampl
e
Constituen
t
Sample Mean
(Minutes)
1 (151,122) 136.5
2 (151,120) 135.5
3 (151,131) 141
4 (122,120) 121
5 (122,131) 126.5
6 (120,131) 125.5
Each of the samples has a probability of occurrence of (1/6)
Hence, sample mean based on the above samples =
(1/6)*(136.5+135.5+141+121+126.5+125.5) = 130.92 minutes
d) In accordance with the central limit theorem, the best estimate of the sample mean is the
population mean which seems to be satisfied in the given case considering the fact that the
sample mean is almost equal to the population mean.
Question 4
The relevant excel screenshot with the answer is shown below.
The formula view for the computations is shown below.

Standard deviation for sample = Population standard deviation/Sample size0.5
Question 5
a) Sample mean = 182.9 lb
The sample standard deviation as per central limit theorem can be indicated as shown below.
The requisite computation of relevant z value is based on the following formula.
Z = (X-μ)/ σ
Z = (140-182.9)/5.77 = -7.44
P (Z>-7.44) = 1-P(Z<-7.44) = 1-0.0001 = 0.9999
b) Sample mean = 182.9 lb
The sample standard deviation as per central limit theorem can be indicated as shown below.
The requisite computation of relevant z value is based on the following formula.
Z = (X-μ)/ σ

Z = (174-182.9)/10.91 = -0.82
P (Z>-0.82) = 1-P(Z<-0.82) = 1-0.2061 = 0.7939
Based on the above computations, it is apparent that the new rating cannot be inferred as safe
considering a significant probability of overloading.
Question 6
Sample proportion (p) = Favourable Cases/Total sample size = 37/125 = 0.296
Standard error = √(p*(1-p)/n) = √(0.296*(1-0.296)/125) = 0.0408
Z value at 95% confidence = 1.96
Margin of error = 1.96*0.0408 = 0.08
Hence, lower limit of 95% confidence interval = 0.296-0.08 = 0.216
Further, upper limit of 95% confidence interval = 0.296 + 0.08 = 0.376
It is apparent that Harris has reported a value of 35% or 0.35 which tends to lie within the
95% confidence interval obtained above and therefore interactive findings of Harris are
validated.