Pre-Calculus Assignment: Functions, Vectors, and Complex Numbers

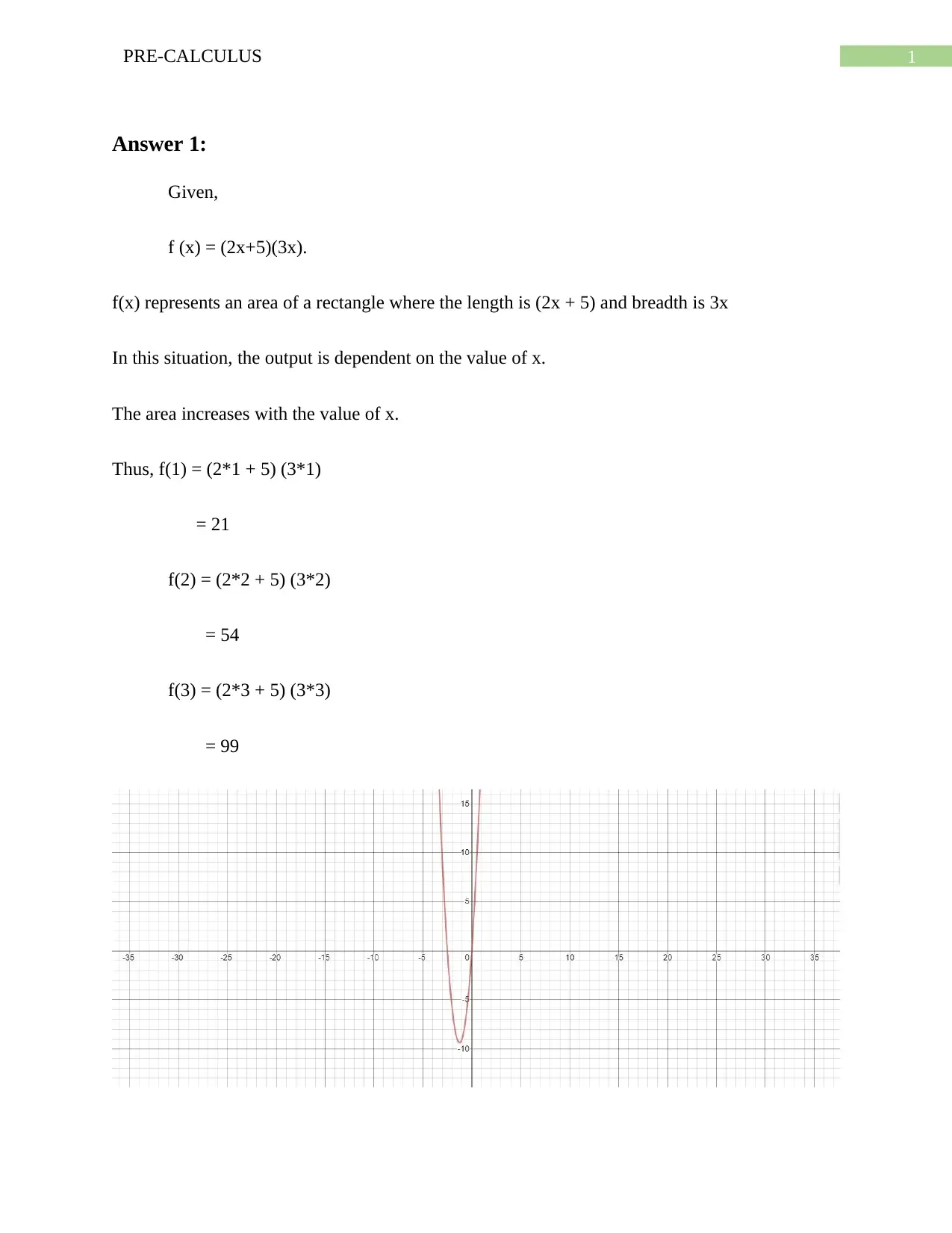
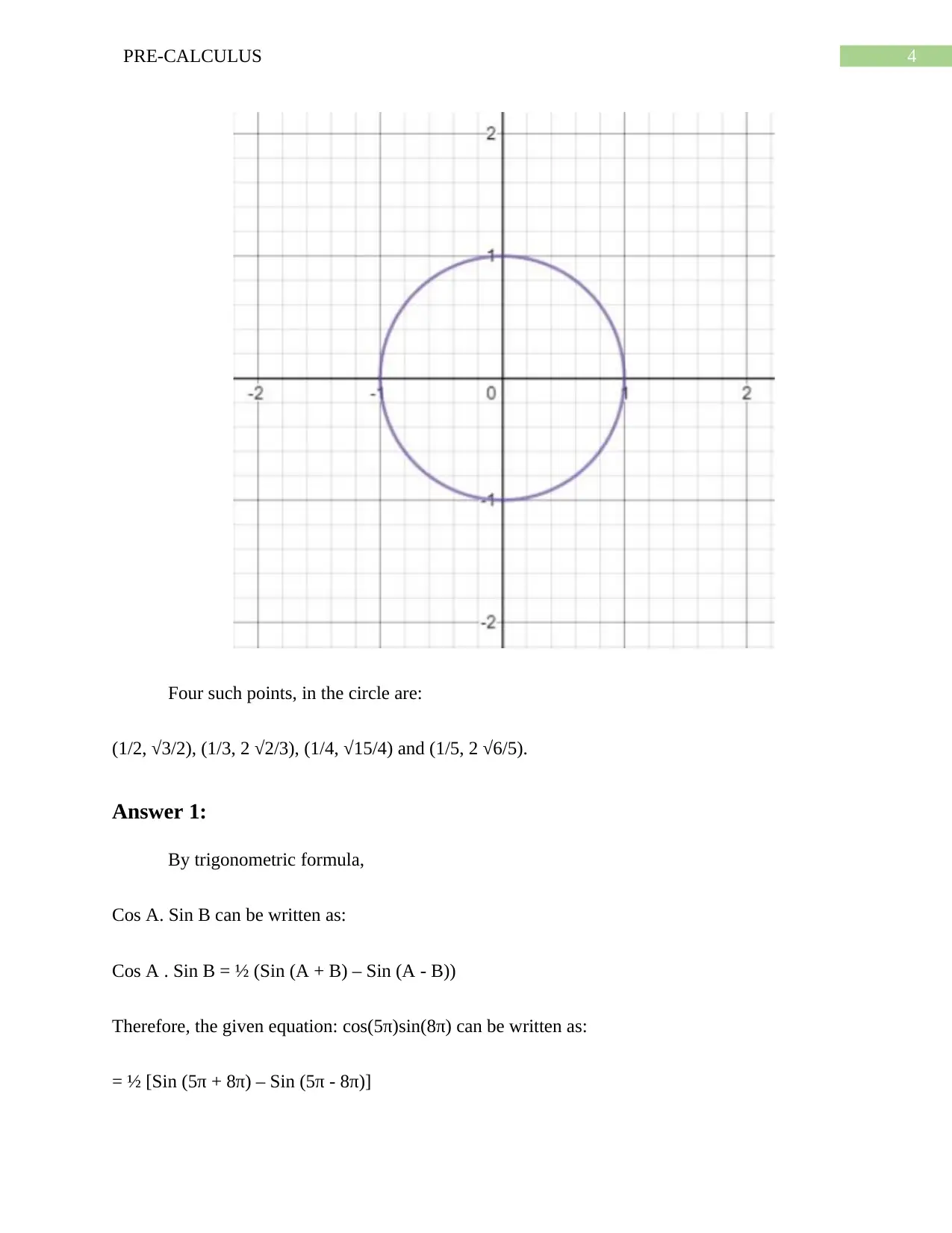
This pre-calculus assignment covers a range of topics including functions, equations, vectors, and complex numbers. The assignment begins with a problem involving a function representing the area of a rectangle, asking for the value of the function at a specific point and its real-world meaning. It then proceeds to solve exponential and linear equations, detailing each step of the solution process. The assignment also explores the unit circle, requiring the identification of points on its circumference and the equation they must satisfy. Furthermore, it utilizes trigonometric identities to simplify a product of trigonometric functions. The assignment also delves into vector analysis, requiring the calculation of a vector's component form and magnitude. Finally, it addresses complex number operations, including multiplication and finding conjugates, with step-by-step explanations. The assignment is a comprehensive review of key pre-calculus concepts, demonstrating problem-solving skills and mathematical understanding.

Running head: PRE-CALCULUS
PRE-CALCULUS
Name of the Student:
Name of the University:
Author Note:

1PRE-CALCULUS
Answer 1:
Given,
f (x) = (2x+5)(3x).
f(x) represents an area of a rectangle where the length is (2x + 5) and breadth is 3x
In this situation, the output is dependent on the value of x.
The area increases with the value of x.
Thus, f(1) = (2*1 + 5) (3*1)
= 21
f(2) = (2*2 + 5) (3*2)
= 54
f(3) = (2*3 + 5) (3*3)
= 99

2PRE-CALCULUS
Answer 2:
In the given function:
f(x) = (2x + 5)(3x),
f(4) = (2*4 + 5)(3*4)
= 13 * 12
= 156
This represents that there is a rectangle whose length is 13 feet and breadth is 12 feet.
Therefore, the area of the rectangle is 156 sq. feet.
Answer 1:
Given equation: 3ex + 2 = 74.
 3ex = 74 – 2
 3ex = 72
 ex = 72/3
 ex = 24
Taking log on both sides,
 loge (ex) = loge (24)
 x = 3.178
Therefore, the value of x is 3.178

3PRE-CALCULUS
Answer 2:
Given, 3-x = 3(6x - 9)
The given equation can be deduced as: -x = 6x – 9 as, [as in equation, ax = ay, it can be written x
= y]
Therefore, -x = 6x – 9
Multiplying -1 in both sides, we get
 x = -6x + 9
 x = 9 – 6x
 x + 6x = 9
 7x = 9
 x = 9/7
 x = 1.28 (approx.)
Answer 3:
The equation of an unit circle is defined as x2 + y2 = 1 [where the center of the circle is
(0,0) and the radius of the circle is 1 unit]
The value of x lies in between -1 and 1
The value of y lies in between -1 and 1

4PRE-CALCULUS
Four such points, in the circle are:
(1/2, √3/2), (1/3, 2 √2/3), (1/4, √15/4) and (1/5, 2 √6/5).
Answer 1:
By trigonometric formula,
Cos A. Sin B can be written as:
Cos A . Sin B = ½ (Sin (A + B) – Sin (A - B))
Therefore, the given equation: cos(5π)sin(8π) can be written as:
= ½ [Sin (5π + 8π) – Sin (5π - 8π)]

5PRE-CALCULUS
= ½ [Sin (13π) – Sin (-3π)]
= ½ [0] {As the value of sin Sin π is 0}
= 0
Answer 2:
The given vector V has the starting point at P(13,-7) and the terminal point of V is (3,-1)
Therefore, the component form of V can be represented as V1 which will be
V1 (3 – 13, -1-(-7))
V1 (-10, 6)
Therefore, the component form of V is (-10, 6)
|V1| = √(-10)2 + (6)2)
|V1| = √136
|V1| = 11.66
|V1| = 10 [round to the hundred unit place]
Therefore the magnitude is 10.
Answer 3:
Applying foil method to calculate the product of the given complex numbers we get:
Two complex number are:
(-7+√7i) and (√7 + i)

6PRE-CALCULUS
(-7+√7i) (√7 + i)
√7 i
√7
i
Therefore, 7 + √7i + √7i +i2
= 7 + 2√7i + (-1)
= 6 + 2√7i
The product of (-7+√7i) and (√7 + i) is 6 + 2√7i
Answer 4:
The given complex numbers are:
A = 3 - 6i and B = 9 + i
(a) The conjugate of A can be written as: A̅ = 3 + 6i [conjugate of a + ib can be written as a - ib]
The conjugate of B can be written as: B̅ = 9 – i [conjugate of a + ib can be written as a - ib]
(b) Sum of A and B can be written as
A + b = (3 – 6i) + (9 + i)
= 3 – 6i + 9 + i
= 12 – 5i
(c) Sum of A̅ and B̅ can be written as:
7 √7i
√7i i2

7PRE-CALCULUS
(3 + 6i) + (9 – i)
= 3 + 6i + 9 – i
= 12 + 5i
(d) By comparing the result of A̅ + B̅ and A + B, we can conclude that the
______
(A + B) = A̅ + B̅
It means that the conjugate of sum is equal to the sum of individual conjugate.