Comprehensive Solution: Principles of Physics Part II Coursework

This document presents a complete solution to a physics coursework assignment, addressing a range of topics within the field of physics. The assignment covers several key areas, including mechanics, projectile motion, wave behavior, and radioactivity. Solutions are provided for problems involving calculations of projectile velocity, acceleration, and range, as well as problems related to forces, moments, and Young's modulus. The document also includes analyses of wave properties, particle behavior, and radioactive decay processes, offering detailed explanations and calculations for each problem. The solution includes calculations, diagrams, and explanations to facilitate understanding of the concepts. The assignment provides a comprehensive overview of the covered physics principles.

Principles of physics
Part II course work
Answer all questions
Q1. AC 1.1
A 240 kg cannon fires a 1.8 kg projectile. Calculate velocity of the projectile if it takes 0.28
seconds to accelerate to its maximum speed, and the cannon recoils, reaching a maximum speed
of 1.4 m/s.
Answer
Let m and M be the masses of projectile and cannon respectively.
If v and V are velocities of the projectile and cannon respectively after firing, then;
Therefore, to find velocity of the projectile;
0= mv + MV
Where;
m- projectile mass
v- projectile velocity
M- cannon mass
V- cannon recoil velocity
0= 1.8 kg x v+ 240 kg x 1.4 m/s
0= 1.8 kg x v + 336 kgm / s
-1.8 kgv = 336 kgm / s
v= (336 kgm / s) / (-1.8 kg)
v= -186.67 m/s
projectile velocity= 186.67 m/s

To find Acceleration;
Acceleration= change in velocity / change in time
Acceleration= (final velocity – initial velocity) / (final time – initial time)
Acceleration= 186.67 m/s – 0 m/s) – (0.28 sec – 0 sec)
Acceleration= 186.67 m/s / 0.28 sec
Acceleration= 666.68 m/s2
Q2. AC 1.1
An archer fires an arrow towards the wall of a castle. The arrow is fired a 45θ from horizontal at a
velocity of 22 m/s. If the wall is 40 m away and stands 7 m tall, calculate whether the arrow will
drop inside the castle walls.
Complete the following:
a. Calculate the maximum height of the arrow
Given that;
Initial velocity= 22m/s
Angle =45θ from horizontal
Using the projectile formula to find height; Hm= (vo. sinθo)2 /2g
Where Hm.is height, is initial velocity and g is earths gravitational acceleration
Then,
Hm= (vo. sinθo)2 /2g
Hm= (22 x sin 45)2 / 2x9.8
Hm= 242/19.6
Hm= 12.35m
b. Calculate the maximum range of the arrow
Given that;
Initial velocity= 22m/s

Angle =45θ from horizontal
Using the projectile formula to find range; R= (vo2. sin 2θ0) / g
Where R is range, u is initial velocity and g is earths gravitational acceleration
Then,
R= (vo2. sin 2θ0) / g
R= (222 x sin 2 (45)) /9.8
R, range = 49.38 m
c. Calculate the vertical height of the arrow as it reaches the wall
Answer
Given that;
Initial velocity= 22m/s
Angle =45θ from horizontal
Using the projectile formula to find the vertical height of the arrow as it reaches the wall
Horizontal and vertical position at time t, each given time
Horizontal position, X.
X= (V0 Cos θo) t
At 40 m where the wall is:
Time of flight to that point will be;
X= (V0 cos θo) t
40= (22 cos 45) t
t= 40 / (22 cos 45)
t= 2.5713 sec.
Y which is the vertical height at that position will be;
Y= (V0 sin θo) t – 0.5gt2
Y= (22 sin 45) 2.5713 – 0.5 x 9.8 x 2.57132
Y= 40 – 32.40
Y= 7.6m
d. Describe the journey of the arrow and whether or not it was successful
Answer

The arrow flight will successfully cross over the wall
Reason
At that point, horizontal distance= 40m, the arrow will be at position 7.6m vertically and
falling towards the ground, while the wall is 7m tall, hence will fly over the barrier which
is the wall, and thus will successfully fly over the wall.
Q3. AC 1.2
A 10 m long seesaw of unknown mass becomes balanced when a 350N child moves the pivot to
a position 3m from one end, and sits 2.4 from the fulcrum.
a. Draw the diagram of the scenario
b. Calculate the mass of the seesaw
Solution
As per the principle of moments, summation of the total clockwise moments is equivalent
to the sum of total anticlockwise moments for a system in balance.
Given that;
The center of gravity is where the gravitational force of the seesaw act at, then;

Center of gravity is in the midway of the seesaw= 10/2 = 5m from each end of the
seesaw. Which is 2m away from the fulcrum.
Sum of Clockwise moments = sum of anticlockwise moments
Summation of Clockwise moments = 2.4m x 350N = 840 Nm
Summation of anticlockwise moments = 2.0m x y= 2.0ym
Let the weight of the seesaw be y
2.0ym=840 Nm
Making y the subject of the formula
y= 840Nm/2.0m
y= 420 newton’s
mass of the seesaw= weight/9.8
mass of the seesaw= 420N/9.8
mass of the seesaw= 42.86 kg
Q4. AC 1.2
A 15m wide horizontal platform is suspended by ropes at each end each capable of withstanding
tension of 112 kN. The uniform concreate has a mass of 1500 kg.
For this question the following formula is used;
Weight= mass x gravitational acceleration
Weight in newton’s= mass x 9.8 m/s2
Calculate the maximum load that can be added to the center of the platform
Solution
Maximum load= maximum load supported by the strings – weight of the concrete
Maximum load= (112kN x 2) – (1500 x 9.8)
Maximum load= 224kN + 14700N
Maximum load= 224000N – 14700N
Maximum load= 209300N
Maximum load= 209.3kN

a. Calculate the maximum load that can be added to the extreme ends of the platform
Solution
Maximum load= maximum load supported a single string – (weight of the concrete / 2)
Maximum load= 112kN – ((1500 x 9.8) / 2)
Maximum load= 112kN + 7350N
Maximum load= 112000N – 7350N
Maximum load= 104650N
Maximum load= 104.65kN
b. Explain why these two calculations produced different values
Answer
For solution (a) the Maximum load= 209.3kN, this is the collective weight which can be
supported by the two stings whenever the weight placed is balanced at the center, while
for (b) the Maximum load= 104.65kN, is the value which can be supported a single string
whether the weight placed on the concrete platform is balanced or not.
c. Suggest a value for a maximum safe recommended load for the platform and justify
Answer
The load should be less than the maximum load, 200kN.
Reason
So as to gather for other effects such as system vibration which might affect the weight of
the load resulting in fluctuation of the weight due to external forces.
Q5. AC 2.1
A 2 kg mass is suspended by a 0.25mm diameter copper wire with Young modulus 117Gpa.
Calculate the extension that will occur if another 1 kg mass is added to this 4.87m long wire.
Answer
Using the formula;
Young modulus= tensile stress / tensile strain

E= (Force / Area) / (change in L /Area)
E= Force x Lenght / A change in Lenght
Where the following initial means;
E- young modulus in Pascal’s
F- force in newton’s
L- original length in meters
δL- change in length area in square metres
δL- change in length in meters
For this case, the formula E= Force x Length / Area x change in Length will be used
E= Force x Length / Area x change in L
Where;
Force= (2+1) x 9.8= 29.4N
Length= 4.87m
Area which is the thickness of the wire; using the formula of area of a circle; πr2
Converting wire thickness to meters= 0.25/1000 = 0.00025m
Then thickness (area) = π x (0.00025/2)2 = 4.9087 x 10-8 m2
117Gpa = (29.4/ 4.87m) / 4.9087 x 10-8 m2 x δl
4.9087 x 10-8 m2 x δl= 6.0370 / 1.17 x 1011
4.9087 x 10-8 m2 x δl= 5.1598 x10-11
δL= 5.1598 x10-11 / 4.9087 x 10-8 m2
δL= 1.05 x 10-3m

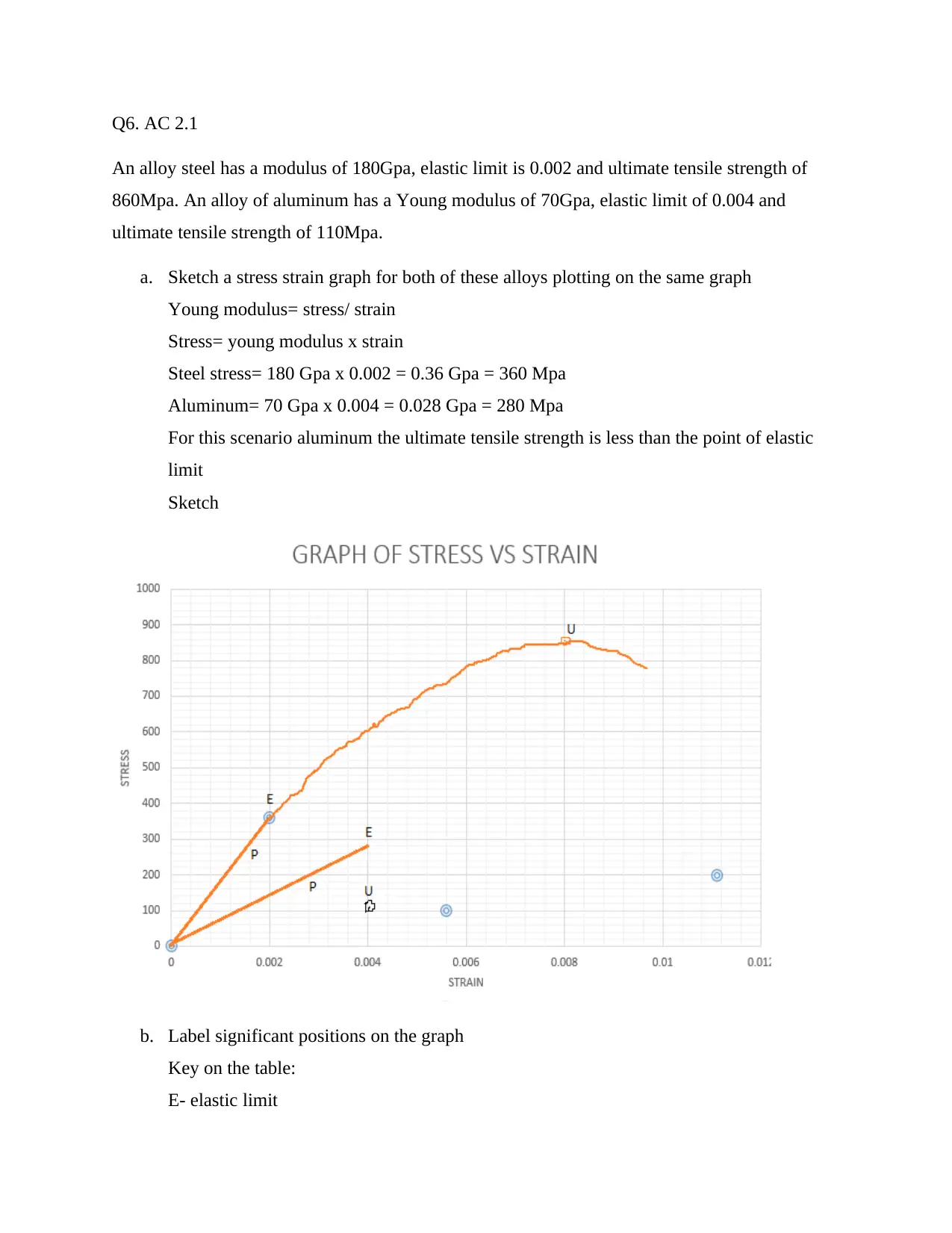
Q6. AC 2.1
An alloy steel has a modulus of 180Gpa, elastic limit is 0.002 and ultimate tensile strength of
860Mpa. An alloy of aluminum has a Young modulus of 70Gpa, elastic limit of 0.004 and
ultimate tensile strength of 110Mpa.
a. Sketch a stress strain graph for both of these alloys plotting on the same graph
Young modulus= stress/ strain
Stress= young modulus x strain
Steel stress= 180 Gpa x 0.002 = 0.36 Gpa = 360 Mpa
Aluminum= 70 Gpa x 0.004 = 0.028 Gpa = 280 Mpa
For this scenario aluminum the ultimate tensile strength is less than the point of elastic
limit
Sketch
b. Label significant positions on the graph
Key on the table:
E- elastic limit

U- ultimate stress point
P- proportional limit
c. Compare and contrast the mechanical properties of these alloys
Answer
Aluminum young modulus= 70Gpa
Steel young modulus = 180Gpa
Their ratios= steel Y. modulus/ aluminum Y. modulus= 180/70 = 2.57
Aluminum is having 2.57 times less young modulus than steel
Aluminum has more elasticity than steel.
Q7. AC 3.1
For each of the following scenarios, sketch the diagrams to show how waves and particles are
expected to behave:
a. Rebounding from a plane boundary
The waves and particles are reflected by the barrier, the angle between the incident waves
and the normal are equal to the angle between the normal and the reflected wave, as
shown in the diagram below.
Diagram

b. Passing through a single narrow slit
The waves and particles bend and spread in an outward manner as they pass through a
narrow slit, as shown in the diagram below.
Diagram
Q8. AC 3.1
Compare and contrast properties of waves and particles, explaining which properties can and
cannot distinguish between a wave-like behavior and particle-like behavior.
Waves Particles
A wave is spread out in space, that is, a wave
is delocalized in space.
Reside in a well-defined position in space,
that is the particle is confined within a given
point at a given time in space
Waves can coexist together at a given point in
space and hence interfere.
A particular point in space is occupied by one
particle at a given time, the same space cannot
be occupied concurrently by more than one
particle at the same time, in other words, the
particles do not interfere with each other.
Presence of a number of waves in a given area
in space may result in interference, and the
A number of particles present in a given
region of space, is equal to their summation of

resulting wave can be greater or lesser in size
than the singular waves. The phenomena can
result in a constructive or destructive
interference.
the individual particles, it is neither less nor
more.
Q9. AC 3.2
Complete the following and comment on your answers:
a. Light passes through two slits 2.7 μm apart and shine on a screen. The first order maxima
occur at angle 9.5θ. Calculate the wavelength of light.
Answer
Using the formula: wavelength, λ= (d/n) sin θ
Where;
n-is the order number,
θ-is diffraction angle in degrees
d-is the expanse between grating lines
2.7 μm = 2700 nanometers
wavelength, λ= (d/n) sin θ
wavelength, λ= (2700/1) sin 9.5
wavelength, λ= 445.63 nanometers
b. Light is incident on metal with work function 2.28 eV. The maximum kinetic energy of
photoelectrons is 0.51 eV. Calculate the wavelength of the light.
Answer
hf= Wn + Ek
where;
h- planks constant
f- frequency of light
Wn- work function
En- kinetic energy

hf= Wn + Ek
6.62607004 × 10-34 J. f= 2.28 eV + 0.51 eV
f= 2.79 eV/ 6.62607004 × 10-34 J
f= 4.210640671 x 1033 Hz
and using the formula V=f. λ
where;
V is the velocity of the wave measure using meters per second.
f is the frequency of the wave measured using Hertz.
λ is the wave wavelength measured using metres.
V=f. λ
3.0 x 108 = 4.210640671 x 1033 x λ
λ =3.0 x 108/ 4.210640671 x 1033
λ =7.12481 x 10-26 m
Q10. AC 4.1
State the formulae of the following radioactive decays
a. Fm100
258 undergoes alpha decay
Solution
Fermium undergoes alpha emission to form Californium as a daughter element
Alpha emission is equivalent to Helium atom ( He2
4 )
Nuclear reaction illustration
Fm100
258 → Cf98
254 + He2
4
b. Te52
136 undergoes beta decay
Solution
Tellurium undergoes beta decay to form Iodine as a daughter element
Beta decay is equivalent to an electron ( e−1
0 )
Nuclear reaction illustration
Te52
136 → I53
136 + e−1
0