Applied Probability and Statistics Calculations Assignment

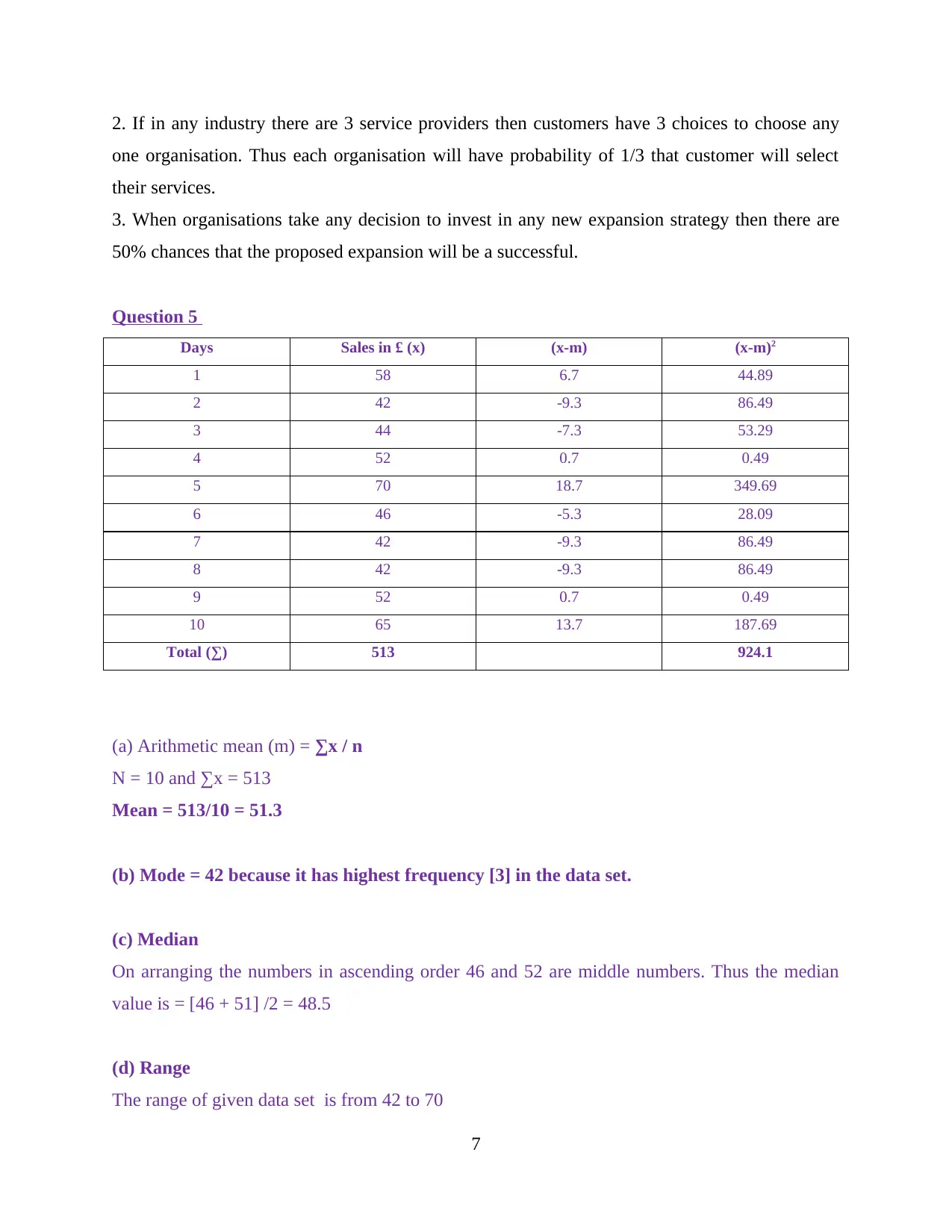
This assignment covers a range of probability and statistics calculations, including basic arithmetic operations, ratio and proportion problems, and probability event analysis. Part A involves calculations such as division, multiplication, addition, and subtraction with both positive and negative numbers, as well as evaluating fractions and percentages. It also includes practical problems related to calculating the number of blue shirts from total production and the number of non-UK students from a total student population. The assignment further explores investment ratio calculations and the importance of probability in business decision-making. Part B focuses on probability events, providing examples like project success/failure, service provider selection, and expansion strategy outcomes. The final question involves calculating the arithmetic mean, mode, median, range, and standard deviation from a given sales dataset, demonstrating practical statistical analysis. This student-contributed document is available on Desklib, a platform offering AI-powered study tools and a wide range of academic resources.

PART A
QUESTION
1. Calculation
(A). 875 / (32 + 42) (2*2+3)
Solution
875 / (9+ 16) (4+3)
875 / 25* 7
875 / 175
= 5
(B). (4410 / 212) (52 / 5)
Solution
(4410 / 441) (25 / 5)
10 *5
= 50
(C). 960 / 12 (1 + 2 * 2) - 302
Solution
960 / 12 (5) - 900
960 / 60 - 900
= 16 – 900
= -884
1

(D). 33 * [(3*5*2 + 62) / (6 + 24)]
Solution
27 * [(30 + 36) / (6 + 16)]
27 * [(66) / (22)]
27 * 3
= 81
(E). [640 / (8+2)] / 82 + 9 -2 + [(42 *2) 2]
Solution
[640 / (10)] / 64 + 9 -2 + [(16 *2) 2]
[64] / 64 + 9 -2 + [64]
1 + 9 -2 + [64]
= 72
2. Calculate
(A). (-33) * (-4)
Solution
+ 132
(B). 46 + (-16)
Solution
+ 50
(C). (-56) /8 - (-9)
Solution
2

-7 + 9
= +2
3. Calculation
(A). ¾ + 3/7
Solution
= [ 3*7 + 3*4 ] / 28
= [21 + 12] /28
= 33/28
= 1.17
(B). 5/8 – 2/5
Solution
= [ 5*5 - 2*8 ] / 40
= [25 - 16] /40
= 9/40
= 0.225
(C). 16/3 + 12/5
Solution
= [ 16*5 + 12*3] / 15
= [80 + 36] /15
= 116/15
= 7.73
3

4. Evaluate
(A). Total production of shirts = 65000
Percentage blue shirts = 32.8%
Solution
Number of blue shirts = [ 32.8 * 65000 ] / 100
= 21320 shirts
Thus there are 21320 numbers of blue shirts
(B). Total students = 28000
Percentage of UK students = 37.6%
Solution
Percentage of Non - UK students = 100 - 37.6 = 62.4%
Number of Non - UK students = [ 28000 * 62.4 ] /100
= 17472
Thus 17472 students are not based in UK
5. Calculate
(A). Ratio of investment = 7: 5: 3: 4
Total investment = £180,500
Solution
Actual investment contributed by each member is:
A = [180500 / 19 ] * 7 = £66500
B = [180500 / 19 ] * 5 = £47500
C = [180500 / 19 ] * 3 = £28500
D = [180500 / 19 ] * 4 = £38000
4

(B). Ratio of investment of x ,y and z = 4: 7: 3
Investment of y = £35000
Solution
Investment made by x = [35000/7 ] * 4 = £20000
Investment made by z = [35000/7 ] * 3 = £15000
Total investment = £35000 + £20000 + £15000 = £ 70000
6. Importance of probability
In business world the important functional and operational decisions always involve
certain extent or amount of risk. Thus before making any decision it is important that extent and
impact of such risk factors must be assessed and analysed so that their consequences can be
eliminated or at least minimised. When decision makers in business are aware of the concept and
application of probability principles then before choosing any strategy or action they will always
determine the success or failure probability. This judgement will help them to decide if the
considered option is profitable or not in regards to investment and risk factors. Hence without
probability knowledge organisations will not be able to distinguish between successful and risky
choices and this may affect their growth and competitive advantage.
PART B
QUESTION 3
(1.) Total number of apples = 550
Number of Green apples (G) = 185
Number of yellow apples (Y) = 215
Number of Red apples (R) = 550 – [185 + 215] = 150
Solution
Probability of green apple = 185/550 = 0.33
Probability of yellow apple = 215/550 0.39
Probability of red apple = 150/550 = 0.27
5

(2.) % buyers of brown bread = 68%
% buyers of white bread = 76%
% buyers of both breads = 54%
Solution
% buyers of atleast 1 bread = % (white bread buyers) + % (brown bread buyers) - % (both
bread buyers)
= 76% + 68% - 54%
= 90%
Thus 90% buyers buy at least one type of bread.
(3.) Total production of machine A = 8350
Damaged items from machine A = 850
Total production of machine B = 9450
Damaged items from machine A = 1030
Solution
Since both the items are picked independently the probability that both items are damaged is
given by:
= Probability of damaged item from A * Probability of damaged item from B
= [850/8350] * [1030/9450]
= 0.101 * 0.108
= 0.010 OR 1%
Thus there is 1% probability that both the items picked will be damaged.
(4.) Probability events
The three examples of probability events in business world are:
1. When organisation starts a new project there are two choices either the project will be
successful or it will be a failure. Each of these events has 50% probability.
6

2. If in any industry there are 3 service providers then customers have 3 choices to choose any
one organisation. Thus each organisation will have probability of 1/3 that customer will select
their services.
3. When organisations take any decision to invest in any new expansion strategy then there are
50% chances that the proposed expansion will be a successful.
Question 5
Days Sales in £ (x) (x-m) (x-m)2
1 58 6.7 44.89
2 42 -9.3 86.49
3 44 -7.3 53.29
4 52 0.7 0.49
5 70 18.7 349.69
6 46 -5.3 28.09
7 42 -9.3 86.49
8 42 -9.3 86.49
9 52 0.7 0.49
10 65 13.7 187.69
Total (∑) 513 924.1
(a) Arithmetic mean (m) = ∑x / n
N = 10 and ∑x = 513
Mean = 513/10 = 51.3
(b) Mode = 42 because it has highest frequency [3] in the data set.
(c) Median
On arranging the numbers in ascending order 46 and 52 are middle numbers. Thus the median
value is = [46 + 51] /2 = 48.5
(d) Range
The range of given data set is from 42 to 70
7

(e) Standard deviation (SD)
Variance = [ ∑ (x-m)2 ] / n
Variance = 924.1 / 10 = 92.41
Standard deviation = √variance
= √92.41
Standard deviation = 9.61
8