Problem Sheet 4: Analyzing Motor Response to Step Input & Constant

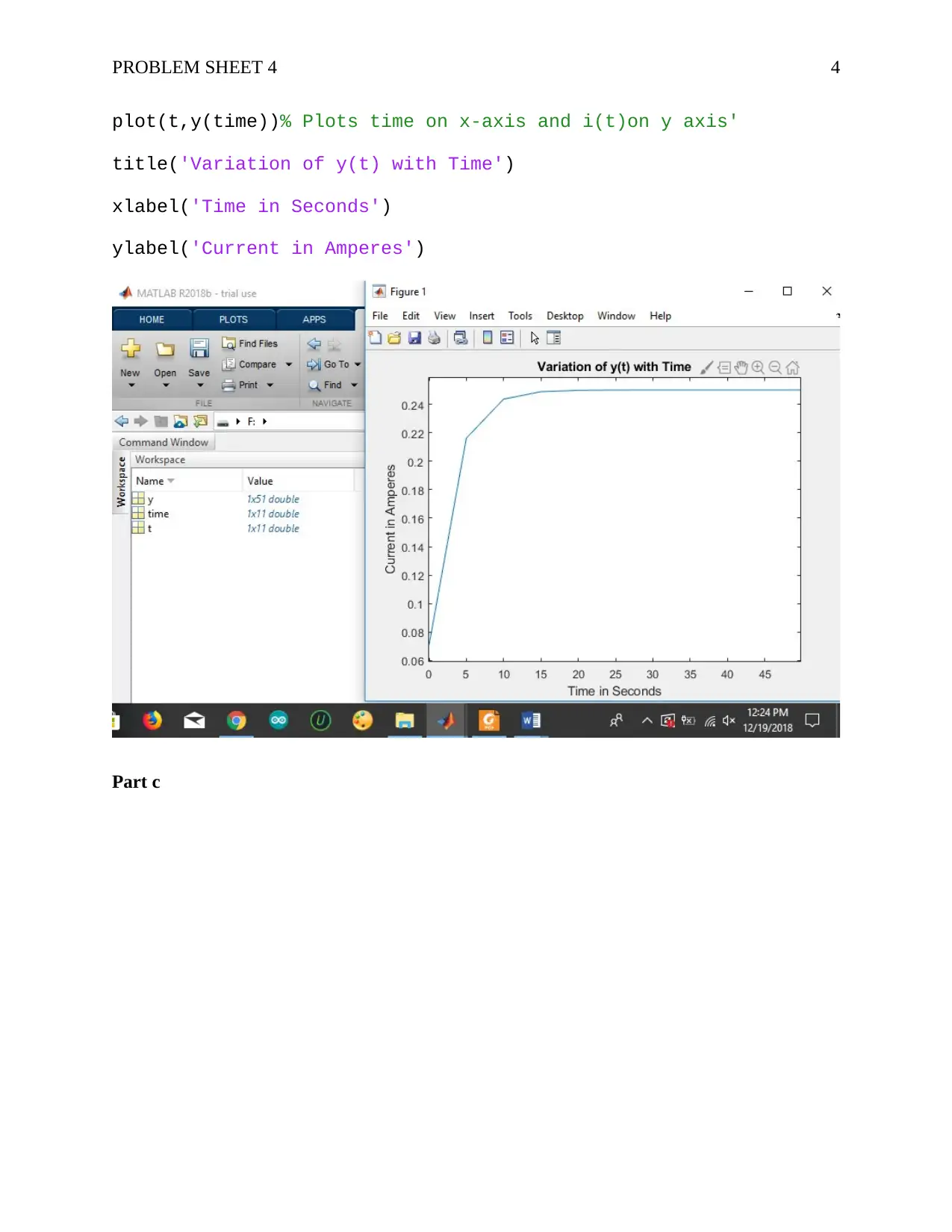
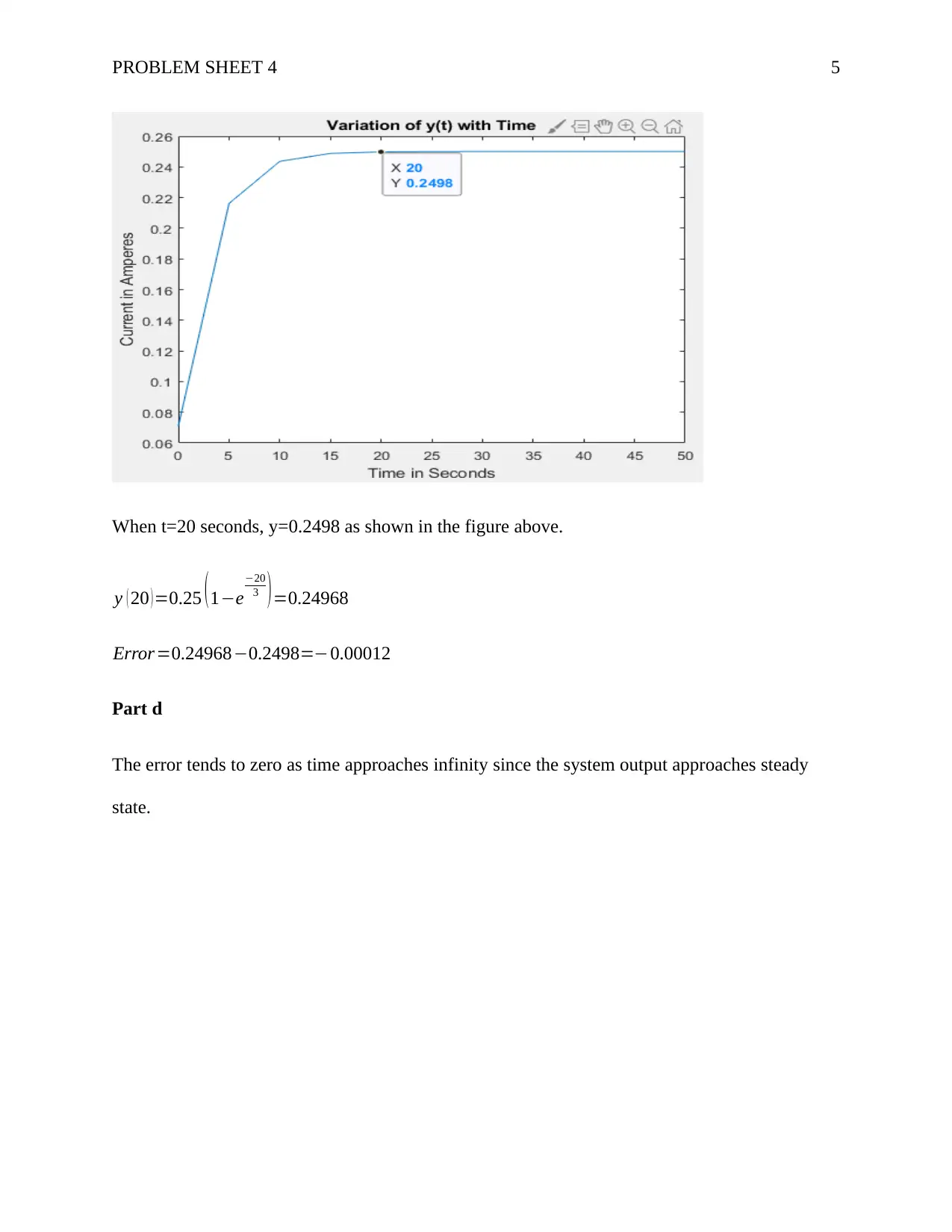
This assignment solution details the analysis of a motor's output (y(t)) in response to a step input (x(t)), with a gain (k) of 1 NM/V and a time constant (T) of 3 seconds. The solution involves determining the expression for Y(s) using Laplace transforms and partial fraction decomposition. It calculates y(t) as 0.25(1-e^(-t/3)). The solution further includes a plot of y(t) versus time from t=0 to 50 seconds, with a calculation of the error at t=20 seconds. Finally, it notes that the error approaches zero as time approaches infinity, as the system reaches a steady state. The assignment utilizes mathematical derivations and graphical representations to illustrate the motor's response characteristics.

Running head: PROBLEM SHEET 4 1
Problem Sheet 4
Name
Institution

PROBLEM SHEET 4 2
Part a
Motor output= y (t), motor input=x (t)
Gain , k=1 NM /V
Time Constant ,T =3 s
x (t ) unit step=0.25 V / s
Y ( s )
X ( s ) = k
1+Ts = 1
1+ 3 s
Y ( s ) = X ( s ) 1
1+ 3 s = 0.25
s ( 1
1+ 3 s )
Y ( s )= 0.25
s (1+3 s )
We split the equation using partial fractions technique to get:
0.25
s (1+3 s)= A
s + B
1+3 s
0.25= A
s × s(1+3 s)+ B
1+3 s × s (1+3 s )
0.25=A (1+3 s )+ Bs
When s=0
0.25=A (1+0)+0
A=0.25
When s=−1
3

PROBLEM SHEET 4 3
0.25=A ( 1+3 ( −1
3 ) ) + B ( −1
3 )
0.25=0− B
3
B
3 =−0.25
B=−0.25× 3=−0.75
0.25
s (1+3 s)= A
s + B
1+3 s = 0.25
s − 0.75
1+ 3 s
Y ( s )= 0.25
s − 0.75
1+3 s
y ( t ) =L−1 {Y ( s ) }=L−1
{ 0.25
s − 0.75
1+ 3 s }
¿ L−1
{ 0.25
s }−L−1
{ 0.75
1+3 s }
¿ 0.25 L−1
{ 1
s }−0.25 L−1
{ 3
1+3 s }
¿ 0.25−0.25 e
−t
3
y (t )=0.25(1−e
−t
3 )
Part b
t=0:5:50;
time=[1:5:51]% initializes time array from 0 to 50 seconds
y(time)=0.25*(1-exp((-1/3)*time)) %#ok<*REDEF> %current equation

PROBLEM SHEET 4 4
plot(t,y(time))% Plots time on x-axis and i(t)on y axis'
title('Variation of y(t) with Time')
xlabel('Time in Seconds')
ylabel('Current in Amperes')
Part c

PROBLEM SHEET 4 5
When t=20 seconds, y=0.2498 as shown in the figure above.
y ( 20 )=0.25 (1−e
−20
3 )=0.24968
Error=0.24968−0.2498=−0.00012
Part d
The error tends to zero as time approaches infinity since the system output approaches steady
state.