Analysis of ABC Ltd. Production: A Business Case Study Solution

This case study analyzes ABC Ltd., a sports equipment manufacturer, aiming to optimize the production of footballs and basketballs to maximize net profit. Using linear programming and Excel Solver, the analysis considers constraints such as machine hours, material costs, and labor costs. The solution determines the optimal production quantities: 40,000 footballs and 56,000 basketballs, resulting in a maximum net profit of $591,840. The report highlights the significant increase in profit compared to the original production levels and provides insights into binding and non-binding constraints, offering recommendations for resource allocation and future profitability. The findings demonstrate the effectiveness of linear optimization in enhancing the company's financial performance.

Running Head: ABC LTD CASE STUDY
1
BUSINESS ANALYSIS CASE STUDY (SL- CONTROL COMPANY)
Name of Student:
Name of Institution:
Date:

ABC LTD CASE STUDY
2
Purpose of the Report
The company called ABC Ltd requires viable production recommendations based on
expert analysis. The recommendations that are required are based on the required number of
balls they should manufacture in order to get optimal profits. Therefore, the analysis involved is
meant to ensure that ABC will obtain maximum net profits from the manufacture and sell of
footballs and basketballs.
The decision to obtain the optimal number of balls that will ensure that the company
gains maximum net profit will be arrived at based on the constraints that the company has. The
constraints include: The capacity of the production, the material costs, the labor costs and the
time available for manufacturing. Constrains are allocated based on the decision variables. The
decision variables are the number of footballs and the number of basketballs that the company
manufactures. Therefore, the report seeks to help ABC Ltd. Improve their resource allocation
processes and decisions.
Description of the Problem
The problem that is being solved in this report is a case study of a production company.
The company is in a dilemma of the optimal units to produce in order get a maximum net profit.
The sporting company has a set of constraints and decision variables that should be used in
making the decision. The description of the scenario is provided in the paragraph that follows.
Methodology
Method that was used to solve the problem is the linear programming method. Linear
programming is a mathematical technique of maximizing variables based on certain constrains.
The maximization is meant to aid decision-making process (Mahmoudi, et al., 2019). The

ABC LTD CASE STUDY
3
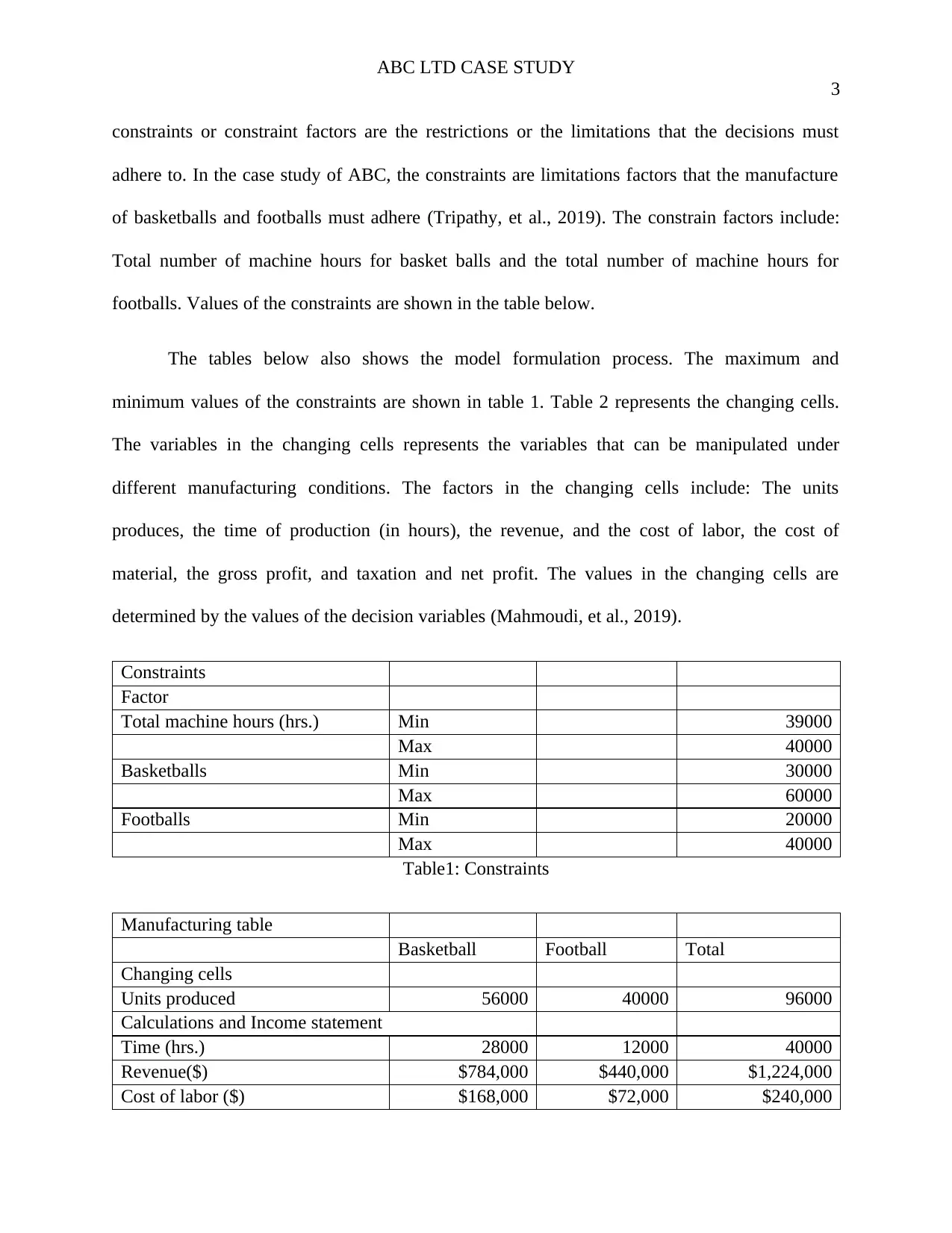
constraints or constraint factors are the restrictions or the limitations that the decisions must
adhere to. In the case study of ABC, the constraints are limitations factors that the manufacture
of basketballs and footballs must adhere (Tripathy, et al., 2019). The constrain factors include:
Total number of machine hours for basket balls and the total number of machine hours for
footballs. Values of the constraints are shown in the table below.
The tables below also shows the model formulation process. The maximum and
minimum values of the constraints are shown in table 1. Table 2 represents the changing cells.
The variables in the changing cells represents the variables that can be manipulated under
different manufacturing conditions. The factors in the changing cells include: The units
produces, the time of production (in hours), the revenue, and the cost of labor, the cost of
material, the gross profit, and taxation and net profit. The values in the changing cells are
determined by the values of the decision variables (Mahmoudi, et al., 2019).
Constraints
Factor
Total machine hours (hrs.) Min 39000
Max 40000
Basketballs Min 30000
Max 60000
Footballs Min 20000
Max 40000
Table1: Constraints
Manufacturing table
Basketball Football Total
Changing cells
Units produced 56000 40000 96000
Calculations and Income statement
Time (hrs.) 28000 12000 40000
Revenue($) $784,000 $440,000 $1,224,000
Cost of labor ($) $168,000 $72,000 $240,000

ABC LTD CASE STUDY
4
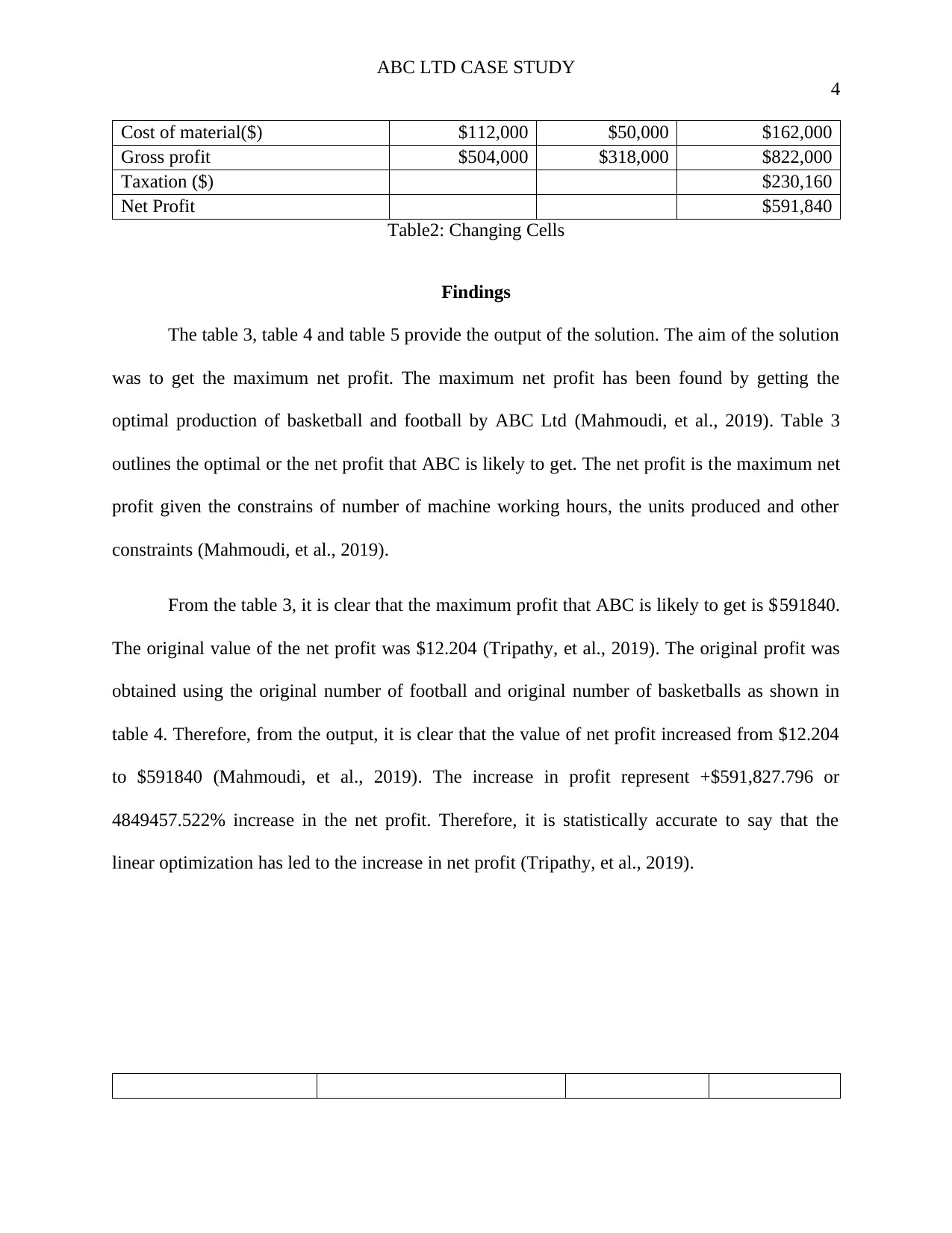
Cost of material($) $112,000 $50,000 $162,000
Gross profit $504,000 $318,000 $822,000
Taxation ($) $230,160
Net Profit $591,840
Table2: Changing Cells
Findings
The table 3, table 4 and table 5 provide the output of the solution. The aim of the solution
was to get the maximum net profit. The maximum net profit has been found by getting the
optimal production of basketball and football by ABC Ltd (Mahmoudi, et al., 2019). Table 3
outlines the optimal or the net profit that ABC is likely to get. The net profit is the maximum net
profit given the constrains of number of machine working hours, the units produced and other
constraints (Mahmoudi, et al., 2019).
From the table 3, it is clear that the maximum profit that ABC is likely to get is $591840.
The original value of the net profit was $12.204 (Tripathy, et al., 2019). The original profit was
obtained using the original number of football and original number of basketballs as shown in
table 4. Therefore, from the output, it is clear that the value of net profit increased from $12.204
to $591840 (Mahmoudi, et al., 2019). The increase in profit represent +$591,827.796 or
4849457.522% increase in the net profit. Therefore, it is statistically accurate to say that the
linear optimization has led to the increase in net profit (Tripathy, et al., 2019).

ABC LTD CASE STUDY
5
Cell Name Original Value Final Value
$D$21 Net Profit Total 12.204 591840
Table 3: Maximum Net Profit
Table 4 represents the output of the optimal production units. The optimal production
units are the number or quantity of decision variables that must be maintained to achieve
maximum output. The optimal production units represents the optimal number of basketballs and
footballs that must be produced in order to maximize the net profit. Therefore, in order to obtain
a net profit of $591840 as indicated in table 3, ABC Ltd. must produce the numbers items below
(Tripathy, et al., 2019). The original number of basketball and footballs that were used for the
maximization were 1 each. The results demonstrate that the optimal number of footballs that the
company should produce in order to get the maximum net profits is 40000. On the other hand,
the optimal number of basketballs that the company should produce in order to get the maximum
net profit is 56000.
Cell Name Original Value Final Value Integer
$B$13 Units produced Basketball 1 56000 Integer
$C$13 Units produced Football 1 40000 Integer
Table 4: Optimal Production Units
Table 5 outlines the statuses of the variables or factors that were used for the
maximization. The factors include: The total time in hours, the total units of basketball that were
produced and the total units of footballs that were produced. The table also shows the factors that
binding and those that are not binding (Tripathy, et al., 2019). A factor is said to be binding if the
amount used in the production is the same as the maximum volume that is available for use. On
the other hand, a factor is said to be non-binding if the amount used in the production process is
less than the total volume that is available for use (Tripathy, et al., 2019).

ABC LTD CASE STUDY
6
The slack is the difference between the biding and non- binding volume of items. In other
terms, the slack is the difference between the cell value and the optimal value. The time is 40000
and the production is 40000. Therefore, the slack is 0 (40000-40000). The value of basketball is
40000 and the value produced is 40000. Therefore, the slack is 0. On the other hand, the units of
footballs that have produced is 56000 while the available volume is 30000. Therefore, the slack
is 26000.
Cell Name Cell
Value
Formula Status Slac
k
$D$15 Time (hrs.) Total 40000 $D$15<=$D
$4
Binding 0
$D$15 Time (hrs.) Total 40000 $D$15>=$D
$3
Not
Binding
1000
$B$13 Units produced
Basketball
56000 $B$13<=$D
$6
Binding 0
$B$13 Units produced
Basketball
56000 $B$13>=$D
$5
Not
Binding
2600
0
$C$13 Units produced
Football
40000 $C$13<=$D
$8
Binding 0
$C$13 Units produced
Football
40000 $C$13>=$D
$7
Not
Binding
2000
0
$B$13:$C$13=Inte
ger
Table 5: Binding/Slack
Conclusions
The report had an aim of obtaining the viable volume of balls (basketballs and footballs) that
ABC Ltd should produce. The optimal volume of footballs and basketballs were determined to
gain maximum net profit. Results optimization demonstrates that it is possible to get a maximum
net profit given the constraints and the decision variables. In order to maximize the net profit,
ABC Ltd should produce 40000 footballs. On the other hand, the optimal volume of basketballs
is 56000.

ABC LTD CASE STUDY
7
References
Mahmoudi, Amin, Liu, Sifeng, Javed, Saad, A., . . . Mehdi. (2019). A novel method for solving
linear programming with grey parameters. Journal of Intelligent & Fuzzy Systems, 2-9.
Tripathy, Archbinda, Subudhi, Robi, N., Patnaik, Srikanta, . . . Jyotiranjan. (2019). Operations
Research in Development Sector || Multi-objective Multi-choice Random Linear
Programming Problem. Journal of Asset Analytics, 2.