PUAD 6060 Homework 4: Regression Analysis, Coefficients, and R-Square
VerifiedAdded on 2019/09/25
|4
|1047
|567
Homework Assignment
AI Summary
This document provides a detailed solution to Homework 4 from PUAD 6060, a political science course, focusing on linear regression analysis. The assignment covers key concepts such as the difference between bivariate and multiple regression, the meaning of regression coefficients, and the interpretation of statistical significance. It explains the R-square statistic and its interpretation as a percentage. The solution also includes an analysis of a provided model, interpreting the explained variation, identifying statistically significant coefficients, and substantively interpreting the impact of independent variables on the dependent variable (Index of Stability). The document references relevant sources to support the analysis.

PUAD 6060 - Fall 2016
Homework 4
1. What is linear regression? Explain the difference between a bivariate, or
simple, linear regression analysis and a multiple regression analysis.
Linear regression is the most commonly used technique for predictive analysis. The
regression is used to explain the relationship between a dependent variable and one or more
independent variables when the relationship between the variables can be described using a
linear model. The value of the dependent variable is predicted from that of the independent
variable (CAMO, 2016).
In a simple or bivariate linear regression analysis, a single independent variable is used to
determine the value of the dependent variable. It is called bivariate linear regression as it
involves only two variables, one dependent and one independent variable.
In a multiple linear regression analysis, two or more independent variables are used to
determine the value of the dependent variable. It is multiple regression analysis as it involves
two or more independent variables and one dependent variable.
2. What do we mean by the term “model” or “regression model?”
A regression model is used to relate the dependent variable (usually represented as Y) with
independent variable (usually represented as X) and unknown parameters (usually
represented as β).
A regression model relates Y to a function of X and β,
Y = f(X, β)
The model includes certain statistical assumptions and the model provides tools for prediction
of the independent variables as well as for finding a solution for the unknown parameters.
3. What are regression coefficients? What does it mean when a
coefficient is statistically significant?
Regression coefficient is the constant which represents the rate of change of the dependent
variable (usually y) as a function of the change in the independent variable (say x). It is the
slope of the regression line.
(y = ax + b)
Homework 4
1. What is linear regression? Explain the difference between a bivariate, or
simple, linear regression analysis and a multiple regression analysis.
Linear regression is the most commonly used technique for predictive analysis. The
regression is used to explain the relationship between a dependent variable and one or more
independent variables when the relationship between the variables can be described using a
linear model. The value of the dependent variable is predicted from that of the independent
variable (CAMO, 2016).
In a simple or bivariate linear regression analysis, a single independent variable is used to
determine the value of the dependent variable. It is called bivariate linear regression as it
involves only two variables, one dependent and one independent variable.
In a multiple linear regression analysis, two or more independent variables are used to
determine the value of the dependent variable. It is multiple regression analysis as it involves
two or more independent variables and one dependent variable.
2. What do we mean by the term “model” or “regression model?”
A regression model is used to relate the dependent variable (usually represented as Y) with
independent variable (usually represented as X) and unknown parameters (usually
represented as β).
A regression model relates Y to a function of X and β,
Y = f(X, β)
The model includes certain statistical assumptions and the model provides tools for prediction
of the independent variables as well as for finding a solution for the unknown parameters.
3. What are regression coefficients? What does it mean when a
coefficient is statistically significant?
Regression coefficient is the constant which represents the rate of change of the dependent
variable (usually y) as a function of the change in the independent variable (say x). It is the
slope of the regression line.
(y = ax + b)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

If a coefficient is statistically significant it means that there exists a significant relationship
between the dependent and the independent variables that is, the change in independent
variable will result in a significant change in the dependent variable.
4 What is the R-square statistic? Explain why it can be interpreted as a
percentage.
R-square statistic is a measure of how close the data is to the fitted regression line. It is
generally known as the coefficient of determination.
R-square can be determined as a percentage as it is defined by the formula,
R-Square = Explained Variation / Total Variation
It is the percentage of response variable variation as explained by the linear model.
A 0% value of R-square indicates that none of the variability of the response data is around
its mean. A value of 100% indicates that all the variability of the response data is around the
mean (Frost, 2013).
5. Using the model and variable definitions presented below, answer
the following questions:
5a. How much variation of the dependent variable does your model
explain? How do you know?
12.3% of the variation of the dependent variable (Index of Stability) is explained by the
model.
We can get this value by looking at the R square value. R square is a statistical measure to
determine how close the data is to the fitted regression line. It can also be defined as
percentage of variation in dependent variables which are explained by independent
variables in a model.
5b. Are any of the regression coefficients statistically significant? Which
coefficients? What is the probability that these relationships are not
random? How do you know?
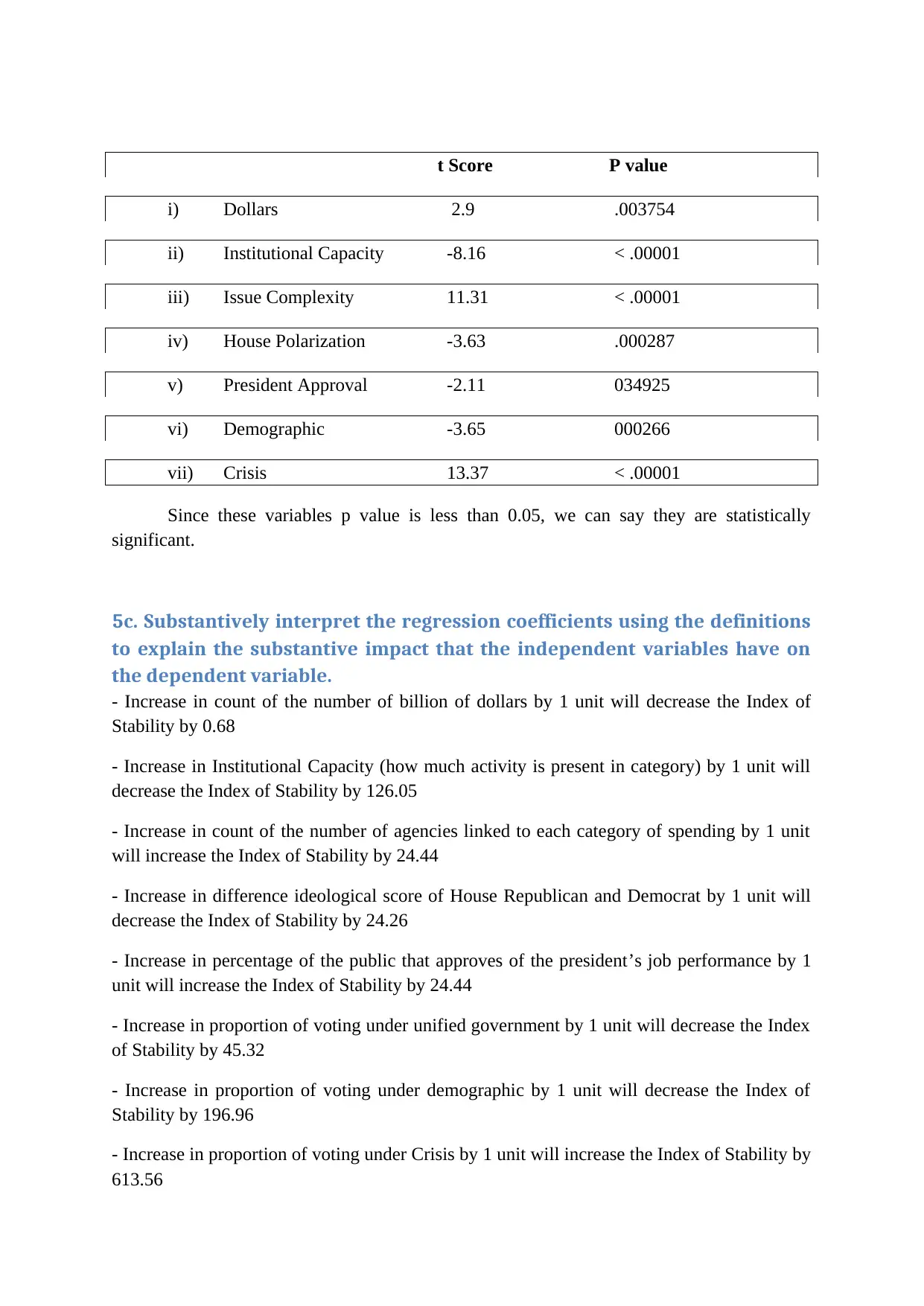
Yes, 7 out of 8 variables are statistically significant.
Taking significance level at 0.05, we can find the p value from t score. T score can be
calculated by dividing the Variable coefficients by respective SE coefficient.
P values of statistically significant variables are mentioned along with their respective t score
below:
between the dependent and the independent variables that is, the change in independent
variable will result in a significant change in the dependent variable.
4 What is the R-square statistic? Explain why it can be interpreted as a
percentage.
R-square statistic is a measure of how close the data is to the fitted regression line. It is
generally known as the coefficient of determination.
R-square can be determined as a percentage as it is defined by the formula,
R-Square = Explained Variation / Total Variation
It is the percentage of response variable variation as explained by the linear model.
A 0% value of R-square indicates that none of the variability of the response data is around
its mean. A value of 100% indicates that all the variability of the response data is around the
mean (Frost, 2013).
5. Using the model and variable definitions presented below, answer
the following questions:
5a. How much variation of the dependent variable does your model
explain? How do you know?
12.3% of the variation of the dependent variable (Index of Stability) is explained by the
model.
We can get this value by looking at the R square value. R square is a statistical measure to
determine how close the data is to the fitted regression line. It can also be defined as
percentage of variation in dependent variables which are explained by independent
variables in a model.
5b. Are any of the regression coefficients statistically significant? Which
coefficients? What is the probability that these relationships are not
random? How do you know?
Yes, 7 out of 8 variables are statistically significant.
Taking significance level at 0.05, we can find the p value from t score. T score can be
calculated by dividing the Variable coefficients by respective SE coefficient.
P values of statistically significant variables are mentioned along with their respective t score
below:
t Score P value
i) Dollars 2.9 .003754
ii) Institutional Capacity -8.16 < .00001
iii) Issue Complexity 11.31 < .00001
iv) House Polarization -3.63 .000287
v) President Approval -2.11 034925
vi) Demographic -3.65 000266
vii) Crisis 13.37 < .00001
Since these variables p value is less than 0.05, we can say they are statistically
significant.
5c. Substantively interpret the regression coefficients using the definitions
to explain the substantive impact that the independent variables have on
the dependent variable.
- Increase in count of the number of billion of dollars by 1 unit will decrease the Index of
Stability by 0.68
- Increase in Institutional Capacity (how much activity is present in category) by 1 unit will
decrease the Index of Stability by 126.05
- Increase in count of the number of agencies linked to each category of spending by 1 unit
will increase the Index of Stability by 24.44
- Increase in difference ideological score of House Republican and Democrat by 1 unit will
decrease the Index of Stability by 24.26
- Increase in percentage of the public that approves of the president’s job performance by 1
unit will increase the Index of Stability by 24.44
- Increase in proportion of voting under unified government by 1 unit will decrease the Index
of Stability by 45.32
- Increase in proportion of voting under demographic by 1 unit will decrease the Index of
Stability by 196.96
- Increase in proportion of voting under Crisis by 1 unit will increase the Index of Stability by
613.56
i) Dollars 2.9 .003754
ii) Institutional Capacity -8.16 < .00001
iii) Issue Complexity 11.31 < .00001
iv) House Polarization -3.63 .000287
v) President Approval -2.11 034925
vi) Demographic -3.65 000266
vii) Crisis 13.37 < .00001
Since these variables p value is less than 0.05, we can say they are statistically
significant.
5c. Substantively interpret the regression coefficients using the definitions
to explain the substantive impact that the independent variables have on
the dependent variable.
- Increase in count of the number of billion of dollars by 1 unit will decrease the Index of
Stability by 0.68
- Increase in Institutional Capacity (how much activity is present in category) by 1 unit will
decrease the Index of Stability by 126.05
- Increase in count of the number of agencies linked to each category of spending by 1 unit
will increase the Index of Stability by 24.44
- Increase in difference ideological score of House Republican and Democrat by 1 unit will
decrease the Index of Stability by 24.26
- Increase in percentage of the public that approves of the president’s job performance by 1
unit will increase the Index of Stability by 24.44
- Increase in proportion of voting under unified government by 1 unit will decrease the Index
of Stability by 45.32
- Increase in proportion of voting under demographic by 1 unit will decrease the Index of
Stability by 196.96
- Increase in proportion of voting under Crisis by 1 unit will increase the Index of Stability by
613.56
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

References
CAMO. 2016. Linear Regression Model. [ONLINE] Available
at: http://www.camo.com/rt/Resources/linear_regression_model.html. [Accessed 1
November 2016].
Jim Frost. 2013. Regression Analysis: How Do I Interpret R-squared and Assess the
Goodness-of-Fit?. [ONLINE] Available at: http://blog.minitab.com/blog/adventures-
in-statistics/regression-analysis-how-do-i-interpret-r-squared-and-assess-the-
goodness-of-fit. [Accessed 1 November 2016].
CAMO. 2016. Linear Regression Model. [ONLINE] Available
at: http://www.camo.com/rt/Resources/linear_regression_model.html. [Accessed 1
November 2016].
Jim Frost. 2013. Regression Analysis: How Do I Interpret R-squared and Assess the
Goodness-of-Fit?. [ONLINE] Available at: http://blog.minitab.com/blog/adventures-
in-statistics/regression-analysis-how-do-i-interpret-r-squared-and-assess-the-
goodness-of-fit. [Accessed 1 November 2016].
1 out of 4
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





