Game Theory: Analysis of Pure Strategy and Subgame Perfect Equilibrium

This assignment delves into game theory, specifically focusing on the concepts of pure strategies and subgame perfect equilibrium (SPE). It begins by identifying the pure strategies for players in a game and then explores mixed strategies. The assignment discusses how a player's state can consist of a subgame and analyzes the paths and payoffs associated with different strategies. It identifies Nash Equilibria and examines the implications of information sets and player incentives. The analysis extends to subgames, determining the optimal actions for players to maximize their payoffs and identifying the subgame perfect equilibrium. The assignment thoroughly explains the steps involved in finding the SPE, defining the SPE path and SPE payoffs within the context of dynamic games and Nash equilibrium.

Statistics
Student Name:
Register Number:
Submission Date:

Table of Contents
Question a........................................................................................................................................................................ 1
Question b........................................................................................................................................................................ 4
Question c........................................................................................................................................................................ 4
References........................................................................................................................................................................ 6

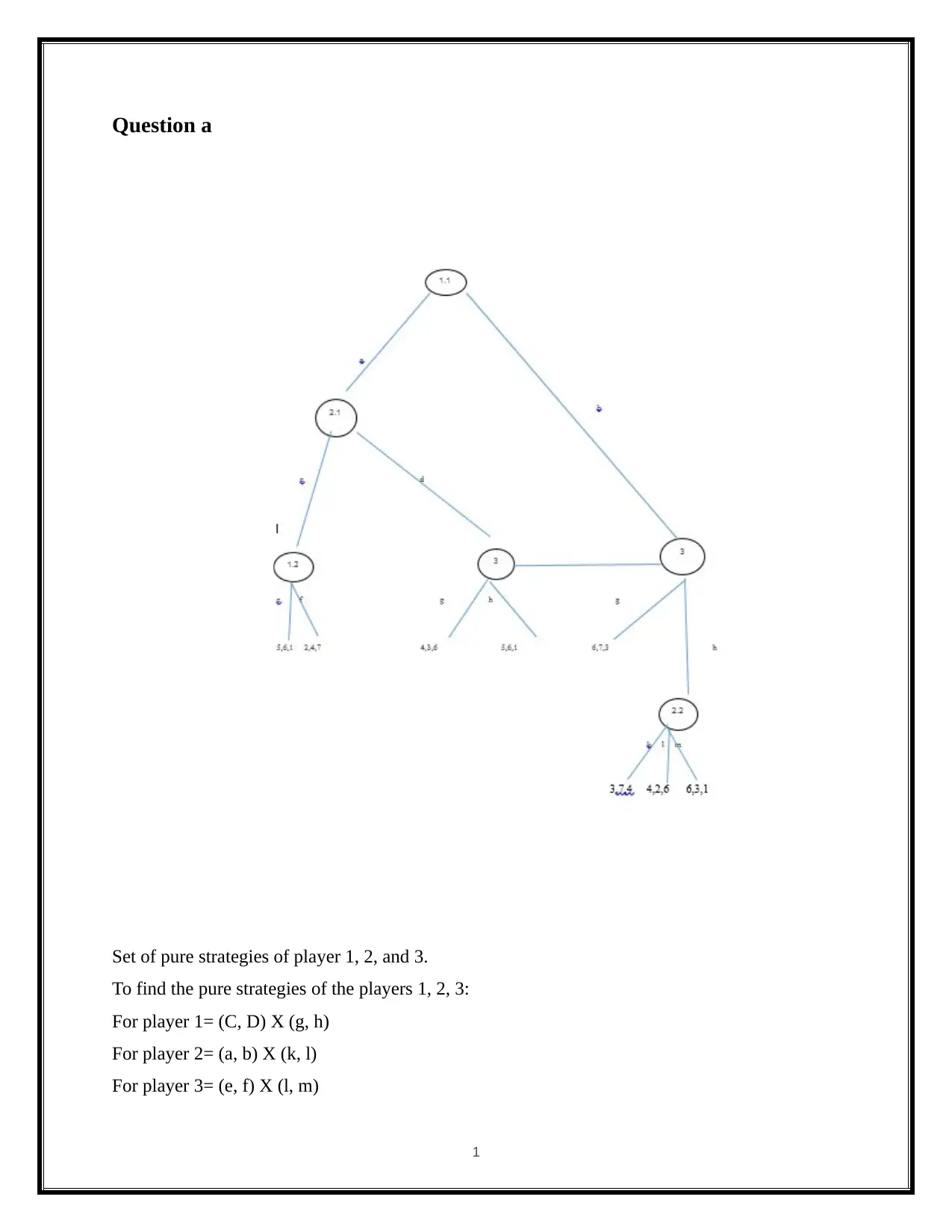
Question a
Set of pure strategies of player 1, 2, and 3.
To find the pure strategies of the players 1, 2, 3:
For player 1= (C, D) X (g, h)
For player 2= (a, b) X (k, l)
For player 3= (e, f) X (l, m)
1

Each player has 6 strategies.
We can find the mixed strategy for Normal game. But, define the probability distribution over the
pure strategies.
If the player state is A, it can consist of sub game.
Player 1
e 5,6,1
f 2,4,7
Player 2
g 4,3,6
h 5,6,1
To find the path on payoff is A.
2

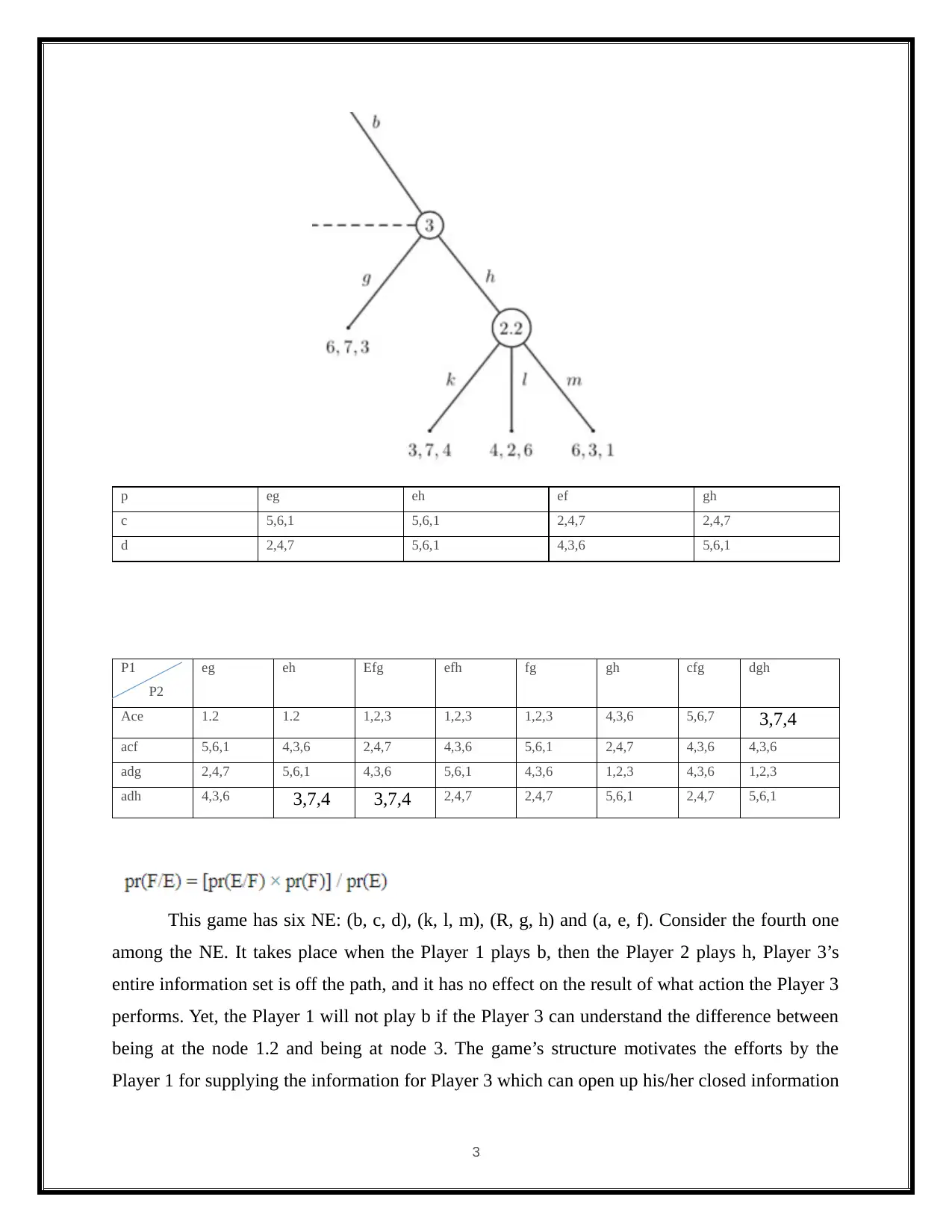
p eg eh ef gh
c 5,6,1 5,6,1 2,4,7 2,4,7
d 2,4,7 5,6,1 4,3,6 5,6,1
P1
P2
eg eh Efg efh fg gh cfg dgh
Ace 1.2 1.2 1,2,3 1,2,3 1,2,3 4,3,6 5,6,7 3,7,4
acf 5,6,1 4,3,6 2,4,7 4,3,6 5,6,1 2,4,7 4,3,6 4,3,6
adg 2,4,7 5,6,1 4,3,6 5,6,1 4,3,6 1,2,3 4,3,6 1,2,3
adh 4,3,6 3,7,4 3,7,4 2,4,7 2,4,7 5,6,1 2,4,7 5,6,1
This game has six NE: (b, c, d), (k, l, m), (R, g, h) and (a, e, f). Consider the fourth one
among the NE. It takes place when the Player 1 plays b, then the Player 2 plays h, Player 3’s
entire information set is off the path, and it has no effect on the result of what action the Player 3
performs. Yet, the Player 1 will not play b if the Player 3 can understand the difference between
being at the node 1.2 and being at node 3. The game’s structure motivates the efforts by the
Player 1 for supplying the information for Player 3 which can open up his/her closed information
3

set. The Player 3 must believe in the provided information, as the game’s structure represents that
the Player 1 has incentive for communicating it straightforwardly. The solution of the game will
then be the SPE of a (now) perfect information game: (L, g2, h3).
The theorists whoever thinks that the game theory is as part of the normative theory of
general rationality. For instance, most of the philosophers and the economists have practiced a
strategy which identifies this solution, based on the basic principles. It is necessary to observe
what the Player 3 in Selten’s Horse thinks when he chooses his strategy.
Question b
 How many sub games does the game have? What are they? Using game theory
 Sub game for actions e and f: player 1 desires to take action e with the payoff (5, 6, 1) for
maximizing the playoff of the player 1. Thus, the payoff action L turn out to be (5, 6, 1).
 Sub game for action C and D: player 2 desires to take action c for 5>2, so the payoff for
action a turn out to be (5, 6, 1).
 Sub game for action g and h: player 2 desires to take action g for maximizing the playoff
of the player 2, so the payoff for action b turn out to be (6, 7, 3).
 Sub game for action k, L and M: player 2 desires to take action k, l, and m for
maximizing the playoff of the player 2. Thus, the payoff action K turn out to be (3, 7, 4).
 Sub game for the action a and b: player 1 will take action a to maximize player 1's payoff.
 Hence, the sub game of perfect equilibrium denotes (Ap, gh) with a payoff (5, 6, 1).
Question c
Determine the set of pure strategy sub game perfect equilibrium (SPE) Explain your steps
carefully?
What is the SPE path and the SPE payoffs?
The sub game perfect equilibrium can be used to find the Nash equilibrium utilized in the
dynamic game of different level of player strategy (Rapoport, 2013). A strategy profile refers to a
sub game perfect equilibrium, if it signifies the Nash equilibrium of the original game’s each sub
game (Owen, 2013).
4

First, the sub game is a 2-person simultaneous game. Nash Equilibrium in pure strategies
are: (h, g) and (a, b). Player 1 has a dominant strategy of No (so d never mixes strategies in a
solution).
If Nash equilibrium doesn't have to be sub game-perfect, the situation is quite a bit more
complicated. Player 2 can threaten to play (2, 4, 7) with non-zero probability 1−p in the left
branch, thus making this branch worth an expected payoff of 5p for Player 1. In the right-hand
branch, as you wrote, Player 1 will always play f and h, and Player 2 can play L with the
probability q and b with probability 1−q, giving an expected payoff of 3q+4(1−q)=4−q to Player
1. There are two types of equilibria, depending on whether Player 1 would prefer A or not. The
preference of Player 1 is A: Here, the Player 2 must choose p=1, since the left-hand branch
actually gets played. q Can be anything, since the right-hand branch doesn't get played and any
value of q lets the Player 1 prefer A if p=1.
5

References
Owen, G. (2013). Game theory. Bingley: Emerald.
Rapoport, A. (2013). Two-Person Game Theory. Newburyport: Dover Publications.
6