Maths Assignment: Analysis of Quadratic Model and Growth Rates

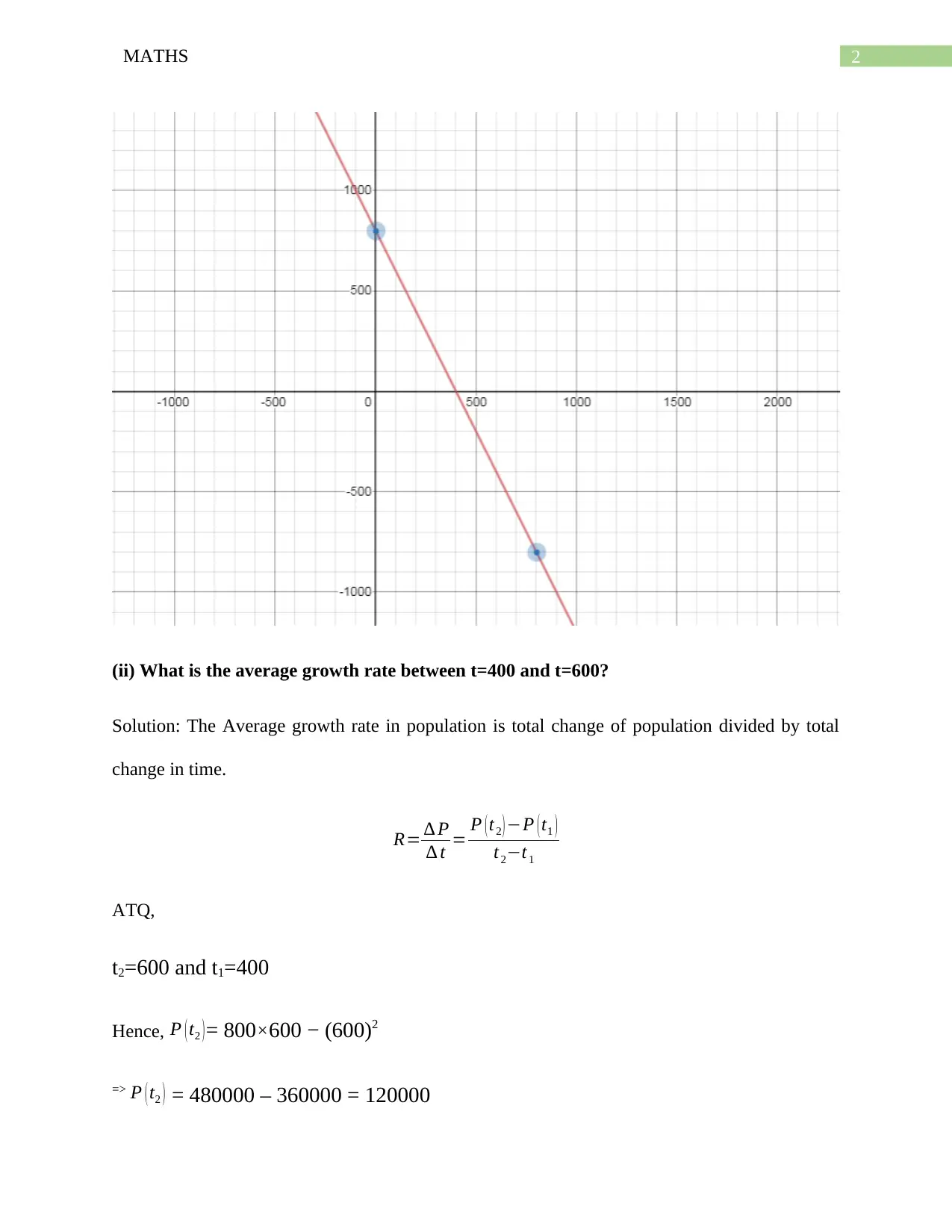
This assignment delves into the analysis of a quadratic model representing a fish population's growth. It explores various aspects, including sketching the model's graph, calculating the average growth rate between specific time intervals, determining the initial growth rate at time t=0, and finding the growth rate at t=600. Furthermore, the assignment identifies the maximum size the population reaches. The solution utilizes derivative calculations to analyze growth rates and provides a comprehensive understanding of the population's behavior over time, showcasing the application of calculus concepts in modeling real-world scenarios. The assignment effectively demonstrates the use of mathematical tools to analyze and predict population dynamics based on the provided quadratic function.

Running head: MATHS
MATHS
Name of the Student
Name of the University
Author Note

1MATHS
A fish population grew according to the following quadratic model: the number of fish on
day t is given by P(t)=800t-t2.
(i) Sketch this model for 0<t<800.
Solution: find the two point line formula for the derivative of the P(t) then plot the graph.
P‘(t) = 800−¿2t
For 0<t<800
Let, P’(t) = y and t = x
Now,
=> y = 800-2x
For x=0, y will be 800
Similar for x = 800, y will be -800
Hence the coordinates, (x1,y1) = (0,800) and (x2,y2) = (800,-800)
Hence, the Graph of the model will be:

2MATHS
(ii) What is the average growth rate between t=400 and t=600?
Solution: The Average growth rate in population is total change of population divided by total
change in time.
R= ∆ P
∆ t = P ( t2 ) −P ( t1 )
t2−t1
ATQ,
t2=600 and t1=400
Hence, P ( t2 )= 800×600 − (600)2
=> P ( t2 ) = 480000 – 360000 = 120000

3MATHS
Similarly,
P ( t1 )= 800×400 − (400)2
=> P ( t1 ) = 320000 – 160000 = 160000
Now, R = 120000−160000
600−200 = −40000
200 = -200 Ans.
(iii) What is the initial growth rate at t=0?
Solution: The growth rate at t=0 will be the first order derivative of the P(t) at t=600.
ATQ,
P(t) = 800t – t2
Differentiating both sides w.r.t x.
=> P' ( t )=800−2 t
Hence at t= 0,
=> P' ( t )=800−2 ×0=800 Ans .(which represents that population was increasing at 800 per day)
(iv) What is the growth rate at t=600?
Solution: The growth rate at t=600 will be the first order derivative of the P(t) at t=600.
ATQ,
P(t) = 800t – t2
Differentiating both sides w.r.t x.

4MATHS
=> P' ( t )=800−2 t
Hence at t= 600,
=> P' ( t )=800−2 ×600=−400 Ans .(which represents the decreasing in population)
(v) What is the maximum size that the population grows to?
Solution: for maximum growth rate the first order derivative of the P(t) will be 0.
Hence,
P(t) = 800t – t2
ATQ,
=> P’(t) = 800 – 2t = 0.
=> 800 = 2t
=> t = 800/2 = 400 ans.
∴ Hence, for t=400 the population will grow at max size.