Quadratic Equation Solver: Java Application Development Project

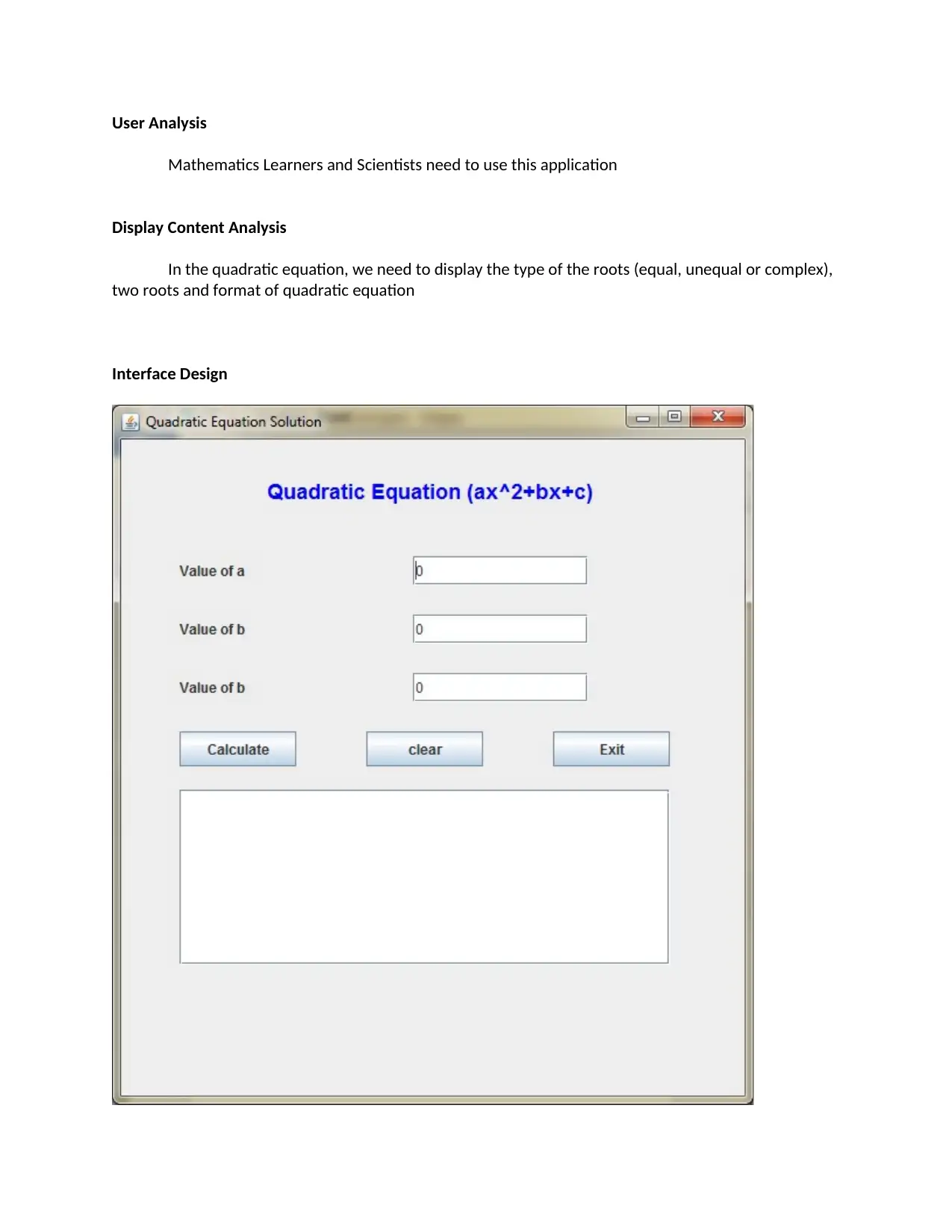
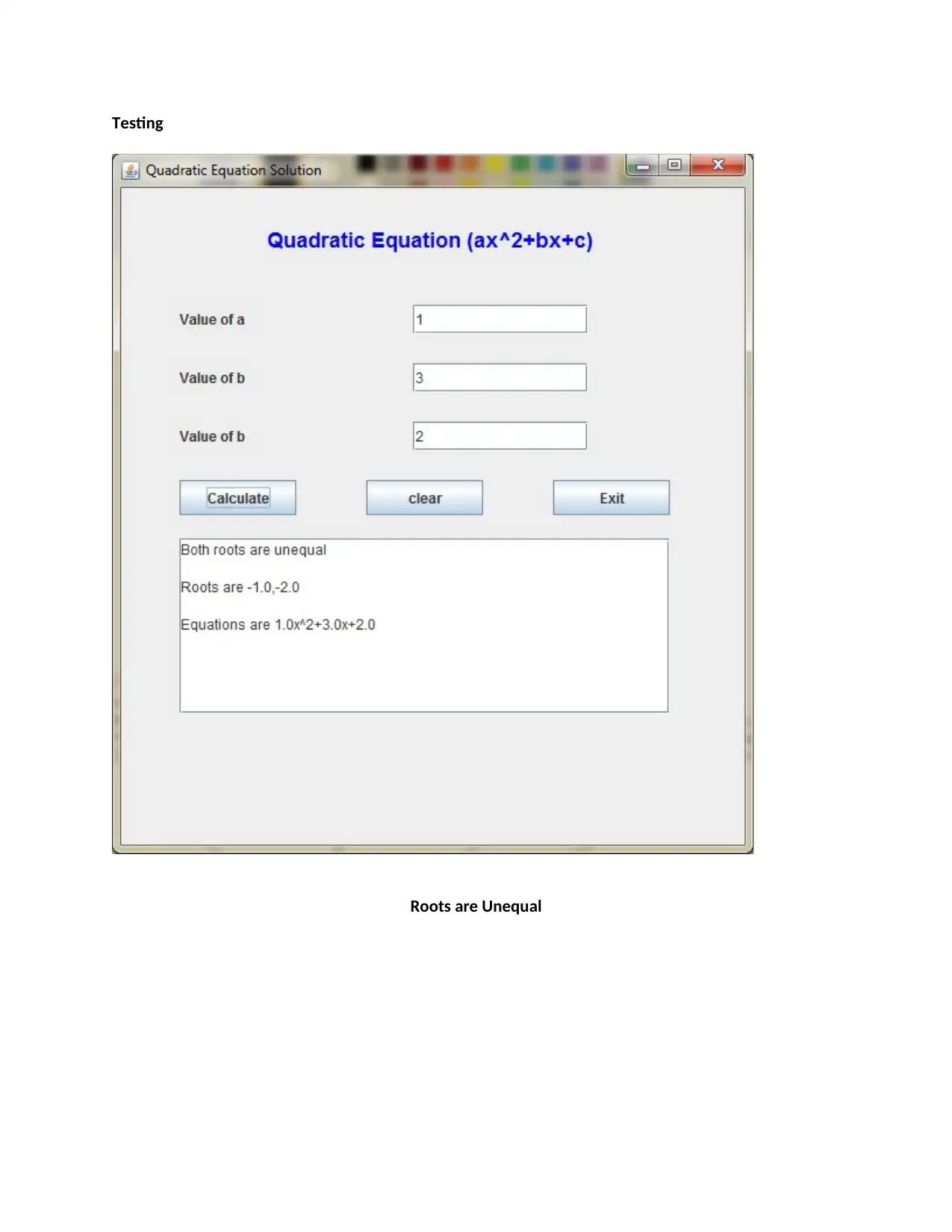
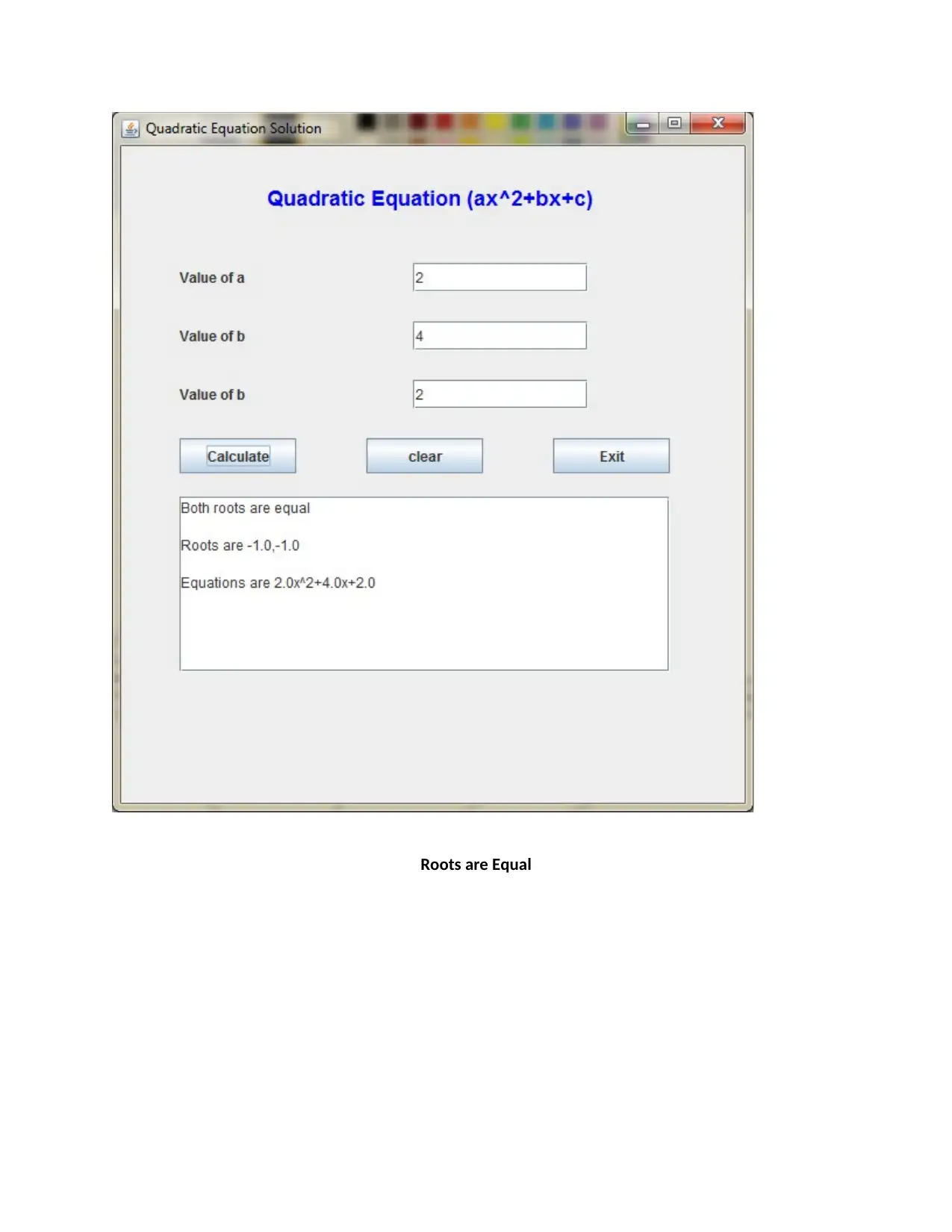
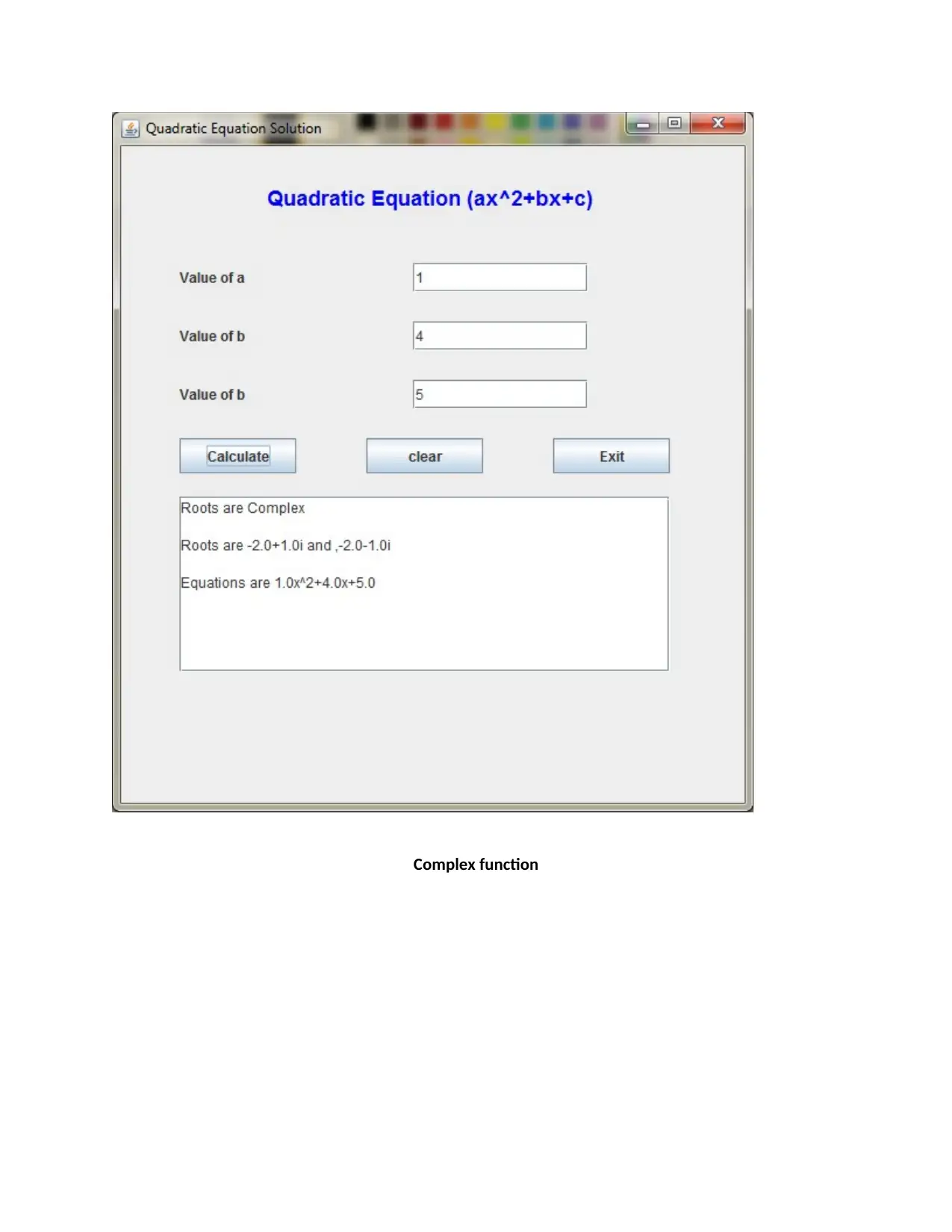
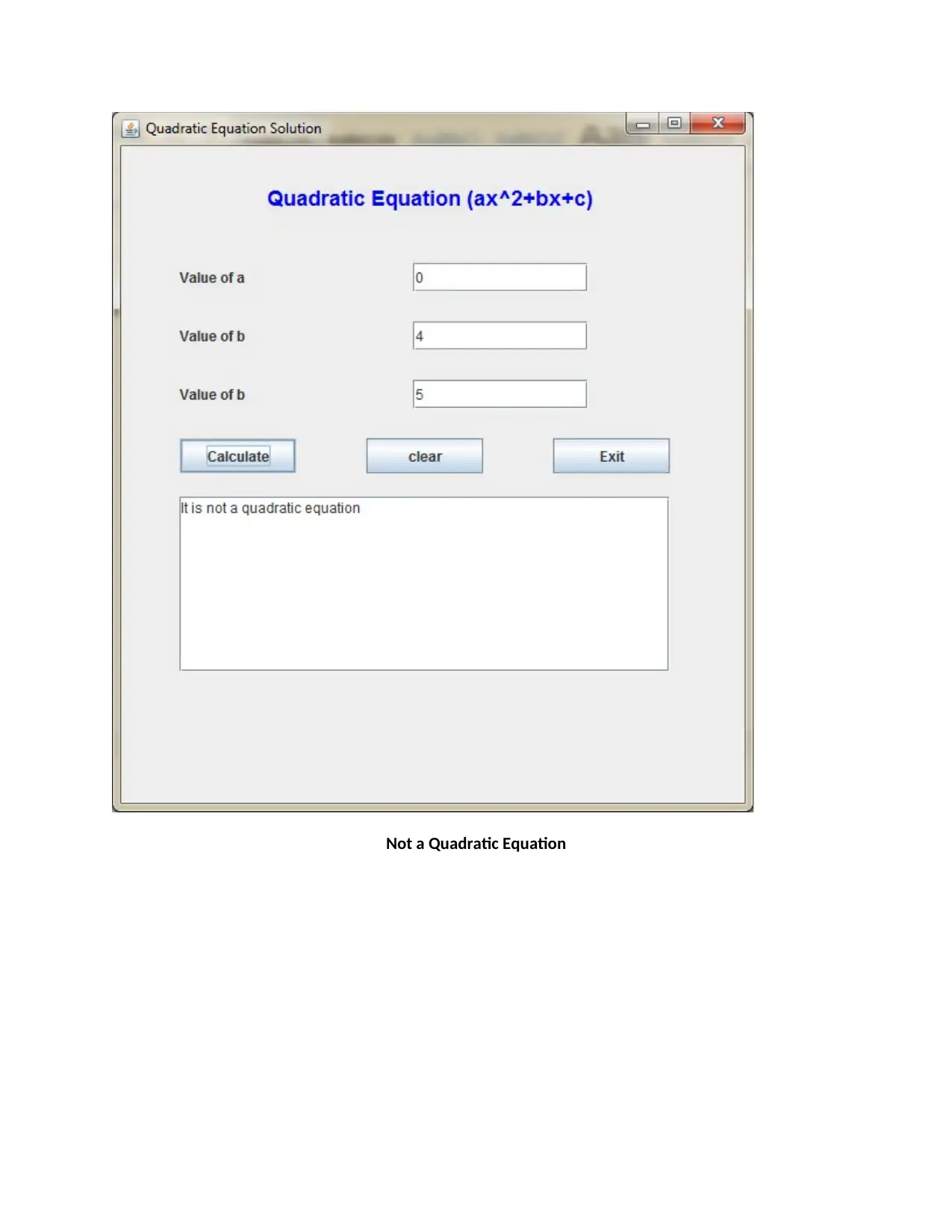
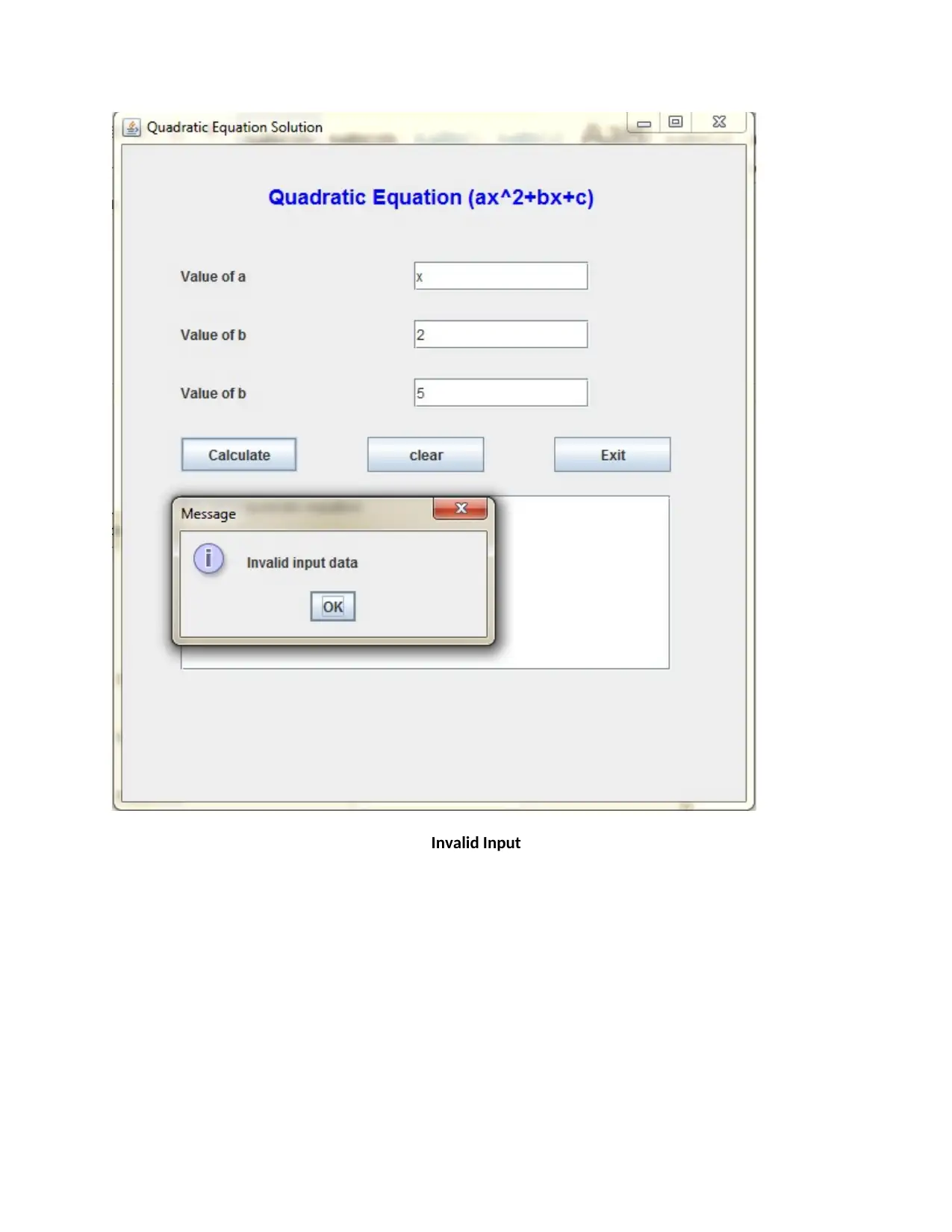
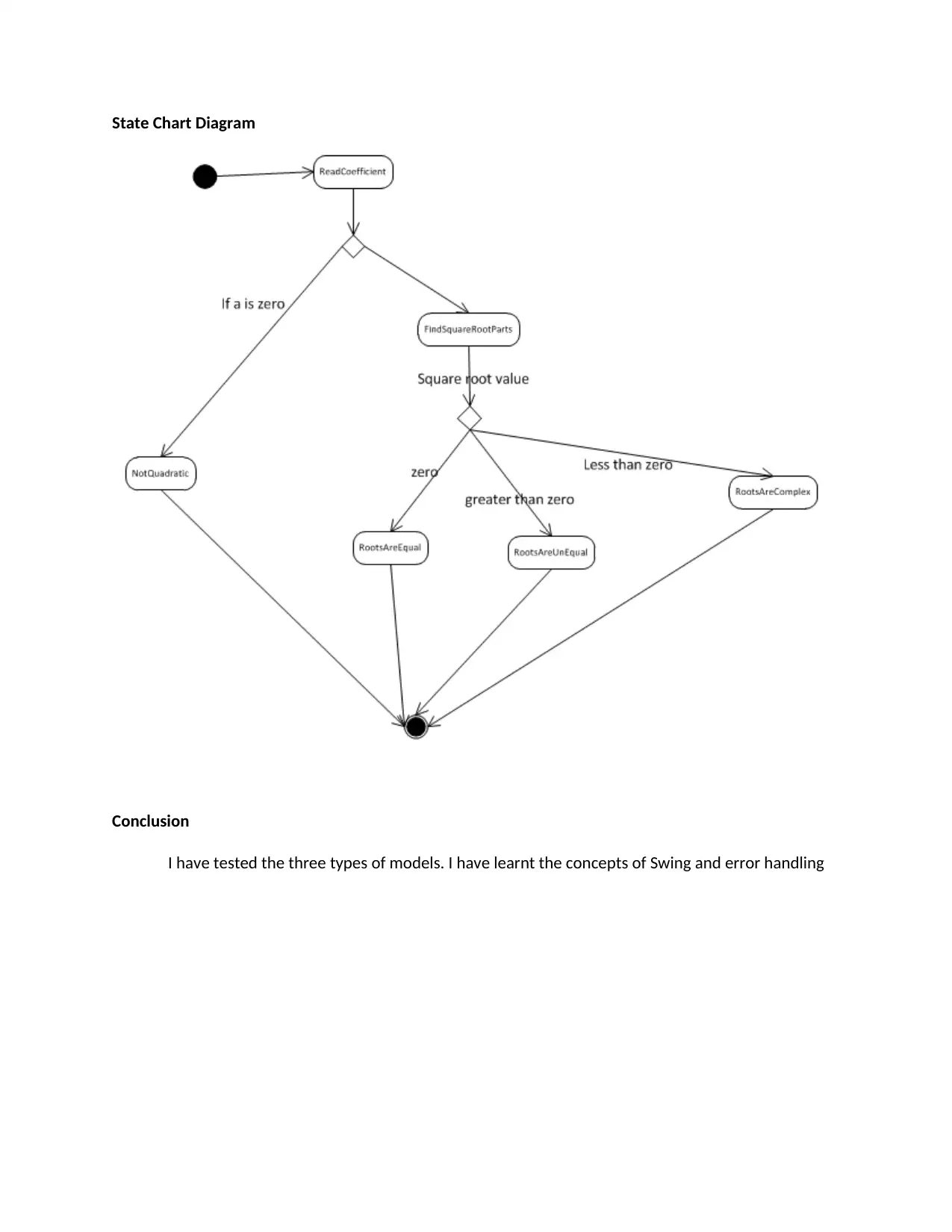
This assignment presents a Java application designed to solve quadratic equations. The application takes input for coefficients (a, b, and c), calculates the discriminant, and determines the nature of the roots (equal, unequal, or complex). The solution includes the Java source code (QuadraticForm.java and Driver.java), describing the user interface design using Swing components, event handling, and error handling to manage invalid input. The code calculates and displays the roots based on the quadratic formula. The assignment also covers testing scenarios, including unequal, equal, and complex roots, along with a state chart diagram to visualize the program's flow. The author employed Java due to its platform independence, robustness, and ease of distribution. This assignment effectively demonstrates the practical application of Java programming in solving mathematical problems with a user-friendly interface.

User Analysis
Mathematics Learners and Scientists need to use this application
Display Content Analysis
In the quadratic equation, we need to display the type of the roots (equal, unequal or complex),
two roots and format of quadratic equation
Interface Design

Modelling of the Problem
For example,
a=1
b=3
c=2
b^2-4ac = 9 – 4 * 1 * 2 = 9 – 8 = 1
-b+sqrt(b^2-4ac) = -3+1=-2
-b-sqrt(b^2-4ac) = -3-1=--4
If a=0, it is not a quadratic equation
If (b^2-4ac) is zero, roots are equal
If b^2-4ac) is greater than zero, roots are unequal
If (b^2-4ac) is less than zero, roots are complex
Description and Justification of Software Tools Chosen
I choose Java Tool to design to solve the quadratic equation. It is an open source, platform
independent, Robust, portability and easy to distribute.

Code
File: Quadratic.java
import java.awt.Color;
import java.awt.Font;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JOptionPane;
import javax.swing.JScrollPane;
import javax.swing.JTextArea;
import javax.swing.JTextField;
public class QuadraticForm extends JFrame implements ActionListener
{
private JLabel lblTitle,lblA,lblB,lblC,lblResult,lblResultEqn;
private JTextField txtA,txtB,txtC;
private JButton btnCalc,btnClear,btnExit;
private JTextArea txtResult;
private JScrollPane scrPane;
public QuadraticForm()
{
lblTitle=new JLabel("Quadratic Equation (ax^2+bx+c)");
lblTitle.setBounds(125,30, 300, 30);
lblTitle.setFont(new Font("Arial",Font.BOLD,18));
lblTitle.setForeground(Color.BLUE);
lblA=new JLabel("Value of a");
lblA.setBounds(50,100, 100, 25);
txtA=new JTextField("0");
txtA.setBounds(250, 100, 150, 25);
lblB=new JLabel("Value of b");
lblB.setBounds(50,150, 100, 25);
txtB=new JTextField("0");
txtB.setBounds(250, 150, 150, 25);
lblC=new JLabel("Value of b");
lblC.setBounds(50,200, 100, 25);
txtC=new JTextField("0");
txtC.setBounds(250, 200, 150, 25);
btnCalc=new JButton("Calculate");
btnCalc.setBounds(50, 250, 100, 30);

btnCalc.addActionListener(this);
btnClear=new JButton("clear");
btnClear.setBounds(210, 250, 100, 30);
btnClear.addActionListener(this);
btnExit=new JButton("Exit");
btnExit.setBounds(370, 250, 100, 30);
btnExit.addActionListener(this);
txtResult=new JTextArea();
scrPane = new JScrollPane(txtResult);
scrPane.setBounds(50, 300, 420, 150);
add(lblTitle);
add(lblA);
add(txtA);
add(lblB);
add(txtB);
add(lblC);
add(txtC);
add(btnCalc);
add(btnClear);
add(btnExit);
add(scrPane);
setLayout(null);
setTitle("Quadratic Equation Solution");
setSize(550,600);
setVisible(true);
}
@Override
public void actionPerformed(ActionEvent e)
{
if(e.getSource()==btnCalc)
{
double a,b,c,sqpart,root1,root2;
try
{
a=Double.parseDouble(txtA.getText());
b=Double.parseDouble(txtB.getText());
c=Double.parseDouble(txtC.getText());
if(a!=0)
{
sqpart= Math.pow(b, 2) - 4 * a * c;
if(sqpart==0)
{
root1=-b/(2*a);
root2=root1;
txtResult.setText("Both roots are equal\
n\nRoots are "+root1+","+root2+"\n\nEquations are "+a+"x^2+"+b+"x+"+c);
}
else if(sqpart>0)

{
root1=(-b+Math.sqrt(sqpart))/(2*a);
root2=(-b-Math.sqrt(sqpart))/(2*a);
txtResult.setText("Both roots are
unequal\n\nRoots are "+root1+","+root2+"\n\nEquations are
"+a+"x^2+"+b+"x+"+c);
}
else
{
sqpart=Math.abs(sqpart);
double f1=(-b)/(2*a);
double f2=(Math.sqrt(sqpart))/(2*a);
txtResult.setText("Roots are Complex\n\
nRoots are "+f1+"+"+f2+"i and ,"+f1+"-"+f2+"i"+"\n\nEquations are
"+a+"x^2+"+b+"x+"+c);
}
}
else
{
txtResult.setText("It is not a quadratic
equation");
}
}
catch(NumberFormatException nfe)
{
JOptionPane.showMessageDialog(null, "Invalid input
data");
}
}
if(e.getSource()==btnClear)
{
txtA.setText("");
txtB.setText("");
txtC.setText("");
txtResult.setText("");
}
if(e.getSource()==btnExit)
{
System.exit(NORMAL);
}
}
}
File : Driver.java
public class Driver
{
public static void main(String[] args)
{
QuadraticForm qform=new QuadraticForm();

}
}

Testing
Roots are Unequal

Roots are Equal

Complex function

Not a Quadratic Equation

Invalid Input

State Chart Diagram
Conclusion
I have tested the three types of models. I have learnt the concepts of Swing and error handling