Quantitative Business Analysis: Homework Assignment Solutions
VerifiedAdded on 2022/09/12
|9
|478
|23
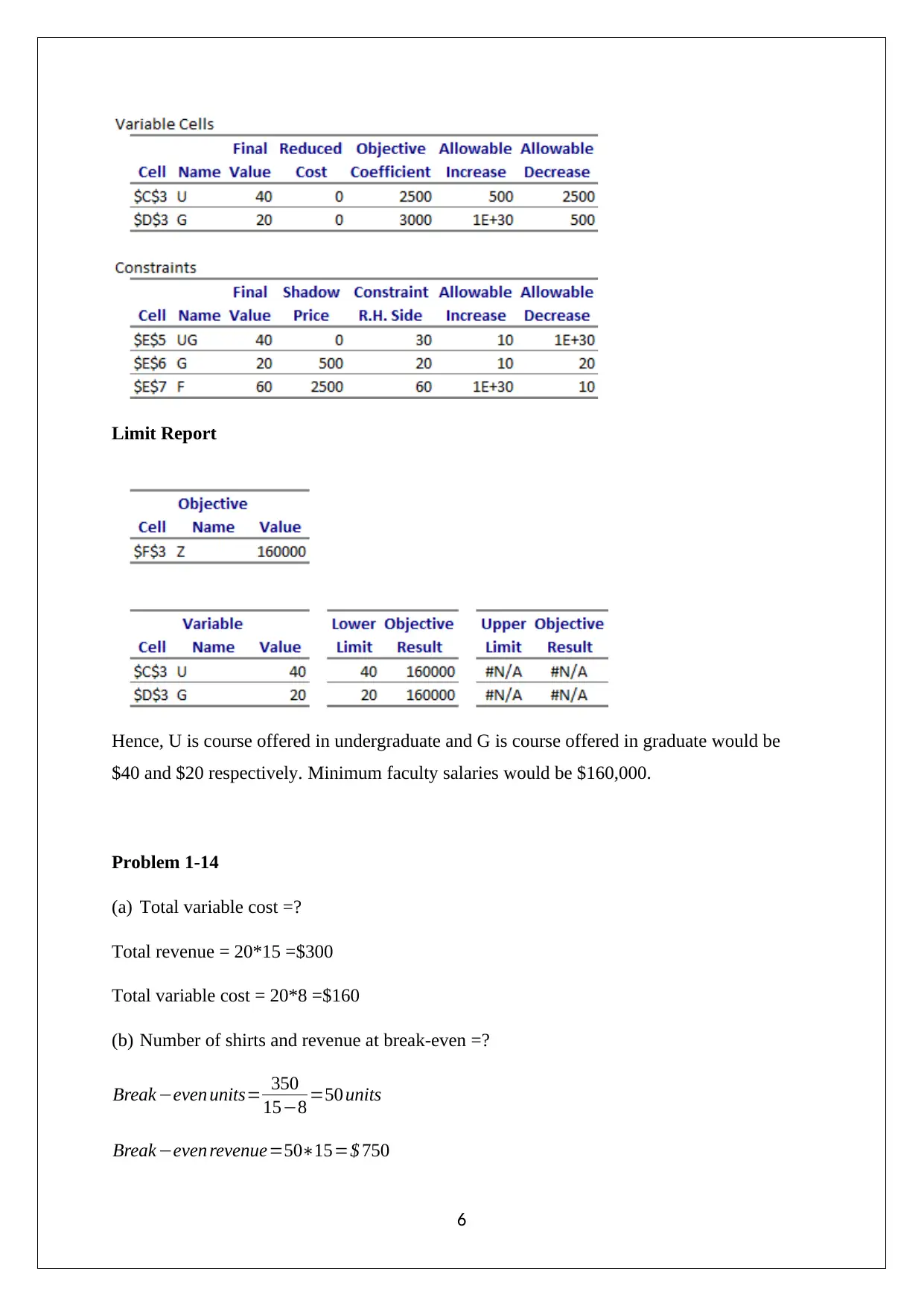
Homework Assignment
AI Summary
This assignment provides solutions to a series of quantitative business analysis problems. The solutions cover topics such as optimal solutions, sensitivity analysis, linear programming, and break-even analysis. The document includes detailed explanations and calculations for each problem, including the use of graphical representations and algebraic equations. Specific problems addressed involve maximizing profit, determining the optimal number of units to produce, and identifying break-even points. The solutions also analyze the impact of changes in variables, such as selling prices and production costs, on the overall financial outcomes. The assignment aims to help students understand and apply quantitative techniques to solve real-world business challenges, providing a comprehensive guide for understanding the key concepts.
1 out of 9






![[object Object]](/_next/static/media/star-bottom.7253800d.svg)