Quantum Mechanics Assignment: Analysis of 1D Potential Well System

This assignment delves into the realm of quantum mechanics, specifically focusing on a one-dimensional potential well. The solution begins by addressing the time-dependent Schrödinger equation across three distinct regions and employs the separation of variables method to derive the wavefunction within a specified region. It then proceeds to determine the general solution for the wavefunction and establishes the relationship between the wave vector and energy. The boundary conditions are applied to derive the solution, followed by the calculation of the normalization constant and energy expression. The assignment further examines the superposition of wavefunctions and the conditions for their normalization, alongside the analysis of a particle's average position and its time dependence. It then extends to the Heisenberg uncertainty principle and the exploration of a two-level system with a dissipative Hamiltonian, including the determination of energy eigenstates and probabilities. Finally, it investigates the time-dependent Schrödinger equation, probability calculations, and simulation of the system's behavior using Julia, providing insights into the probabilities of finding the system in different states.

1
Quantum Mechanics
Name
Institutional Affiliation

2
One Dimensional Potential Well
Assume a quantum particle in 1D subjected to the potential defined as
V ( x )= { ∞ for x <0
0 For 0< x < L
∞ for L< x
1. Write the time-dependent Schrödinger equation in the three regions naturally
separated.
iℏ ∂ ψ (x ,t)
∂ t =−ℏ2
2 m
∂2 ψ ( x , t)
∂ x2 +V (x ,t )ψ (x ,t )
2. Use the method of separation of variables to show that the wavefunction of
the system in the region 0 ≤ x ≤ Lcan be written as Ψ ( x , t )=ψ ( x ) f ( t ) , for
which the time-dependent Schrödinger equation becomes
iℏ ∂t f (t )
f (t ) =E And −ℏ2
2m
∂2 ∂x
2 ψ ( x )
ψ ( x ) =E
¿ separation variable method Ψ ( x , t ) is a product of 2 functions∧each is
a function of only 1 variable .
ψ ( x , t ) =ψ ( x ) f (t)
Putting into Schrö dinger' s equation yields
iℏ ∂ f ( t )
∂ t ψ ( x ) =−ℏ2
2 m
∂2 ψ ( x )
∂ x2 f (t )+V ( x , t)ψ (x) f (t)
dividing by ψ
iℏ ∂ f (t)
∂ t
1
f (t) =−ℏ2
2 m
∂2 ψ ( x )
∂ x2
1
ψ ( x )+V ( x , t )
Considering potentialthat do not explicitly depend on time
V ( x , t ) =V ( x )

3
iℏ ∂ f (t)
∂ t
1
f (t) =−ℏ2
2 m
∂2 ψ ( x )
∂ x2
1
ψ ( x ) +V (x )
each side depends only on one variable
iℏ ∂ f (t)
∂ t
1
f (t) =E= iℏ ∂t f (t )
f (t) =E
−ℏ2
2m
∂2 ψ ( x )
∂ x2
1
ψ ( x ) +V ¿ =E
3. Show that the most general solution for the wavefunction ψ ( k ) is given by
ψ ( k ) = A sin ( kx ) + B cos (kx ),
And write explicitly the relation between the wave vector k and the energy E.
For x ≥0 x ≤ L E>V =0
−ℏ2
2m
∂2 ψ
∂ x2 = (E−V )ψ Let ψ ( x ) = A ebx
⟹ b=± jk where kℏ =P= √2 m( E−v)
k = √2m ¿ ¿ ¿
ψ ( x ) = A e±ikx
ψ ( k ) = A sin ( kx ) + B cos (kx ),
Relationship between the wave vector k and the energy E
k = √2 m( E−v )
ℏ
4. Use the boundary conditions of the problem to deduce that the solution must
be
ψn ( x ) =A sin ( n πx
L ), with n∈ z
Using boundary conditions

4
ψ ( x=0 ) =0⟹ A=0 ψ ( x=L ) =0 ⟹ ± AsinkL=0
⟹ sin kL=0 And k n L=nπ
k n= nπ
L = √2 m En
ℏ En =( ℏ n π
L )2 1
2 m ,t= ℏ
2 π
En =( ℏ n π
L )
2 1
8 m ,ψn ( x ) =A sin ( n πx
L ), with n∈ z
5. Find the normalization constant A and write the energy En in terms of n
1=∫
−∞
∞
│ψn ( x ) │2 dx
¿ A2
kn
∫
0
nπ
(sin ∝)d ∝ = A2
kn
∫
0
nπ
1
2 (1−cos 2∝)d ∝
A2
kn
¿
1
2
A2
nπ
L
( nπ−sin (2nπ )
2 ) =
A2
2
L
=1
A= √ 2
L
ψn =
{√ 2
L
0
sin nπx
L 0 ≤ x ≤ L and x ≤ 0 , x ≥ L
En =( nℏ
L )
2 1
8 m
6. Show that the wavefunction Ψ ( x , t )=ψn ( x ) ei E nt / h and therefore their linear
Superposition.

5
ψ ( x , t )=∑
n
αn ψn(x) e
−i E n t
ℏ
Withα n ϵ C, are solutions to the time-dependent Schrödinger equation.
iℏ df (t )
dt =Ef (t)
df (t)
f (t ) =−iE
ℏ dt
∫ df (t )
f (t) =∫ −iE
ℏ dt
log f ( t ) =¿ iE
ℏ t+C ¿
Incorporating the constant C into ψ
f ( t )=e
−iEt
ℏ
ψ ( x , t ) =ψn(x) e
i En t
ℏ
¿ linear superposition
ψ ( x , t )=∑
n
α n ψn(x) e
−i E n t
ℏ
7. What condition must satisfy the coefficients αn ,so that the wavefunction above
is normalized?
i. The function must be single valued
ii. It must be a finite value
8. Consider a particle occupying the state given by the superposition

6
ψ ( x , t )= 1
√1+ β2 [ ψ1 ( x ) e−i w1 t + β ψn ( x ) e−i wn t
]
With w1= Ei
ℏ and 0≤ β ≤ 1
a. Show that the average position of the quantum particle is given by
⟨ x ⟩ = L
2 −8 Lnβ ¿ ¿cos⌊ ( wn−w1 ) t ⌋
In which case s is this mean value independent of time?
The positionof x expected value is defined as ⟨ x ⟩ = L
2 ∫
−∞
∞
ψ ( x , t ) xψ ( x , t ) dx
⟨ x ⟩=│ ψ │ x │ψ │
= L
2 ∫
0
L
1
√ 1+ β2 [ ψ1 ( x ) e−i w1t +β ψn ( x ) e−i wn t
]dx
L
2 [ 1
√1+β2 [ ψ1 ( x ) e−i w1 t + β ψn ( x ) e−i wn t
] ]L
L
2 −¿
⟨ x ⟩ = L
2 −8 Lnβ ¿ ¿cos ⌊ ( wn−w1 ) t ⌋
b. Show that ⟨ x2 ⟩ , ⟨ p ⟩ ∧ ⟨ p2 ⟩ are given by the following
⟨ x2 ⟩ = 1
2 ⟨ ψ │a2 + at2
+a at +at a │ψ =
L2
12(1+ β2 ) ¿
=¿dx
= L2
12(1+ β2 ) ¿

7
⟨ p ⟩ =4 ¿ ¿
⟨ p ⟩=¿ ∫
0
L
ψ ( x , t) ℏ
i
∂
∂ x ψ ( x , t ) dx
⟨ p ⟩ =│ ψ │ x │ ψ │
⟨ p ⟩ =∫
0
L
1
√ 1+ β2 [ ψ1 ( x ) e−i w1 t + β ψn ( x ) e−i wn t
]
2
L [ 1
√ 1+β2 [ ψ1 ( x ) e−i w1 t + β ψn ( x ) e−i wn t
] ] L
4 ℏ nβ
L2 √1+ β2 ¿
⟨ p ⟩ =4 ¿ ¿
⟨ p2 ⟩ =ℏ2 π2 ¿ ¿
⟨ p2 ⟩=1
2 (2 at a−1−a2−at2
)
¿ ¿dx) ^2
1
2 ( 2 at a−1−a2−at2
) =∫
0
L
( 1
√ 1+β2 )
2
[ ψ1 ( x ) e−i w1 t + β ψ n ( x ) e−i wn t
] 2
¿∫
0
L
( 1
√ 1+ β2 )
2
[ ψ1 ( x ) e−i w1 t + β ψn ( x ) e−i wnt
] 2
¿ ℏ2 π2
L2 ¿
⟨ p2 ⟩ =ℏ2 π2 ¿ ¿
c. Obtain σ x and σ p. Does this state satisfy the Heisenberg uncertainty principle? What
n and β allow to get the closest to this fundamental limit?
σ x =√ ⟨ x2 ⟩ − ⟨ x ⟩ 2
σ x =√ ¿ ¿

8
√¿ ¿ −¿
σ p=√ ⟨ p2 ⟩ − ⟨ p ⟩ 2
¿ √ ¿ ¿
√ ¿ ¿ -¿
The uncertainty position∧momentum are consistent withthe uncertainty principle
thus they satisfy Heisenbergy uncertainty principle.
A dissipative Hamiltonian
Consider a so-called two-level system. In the basis of | g ⟩ and | e ⟩ (the ground and
excited states, respectively), the Hamiltonian describing the dynamics of the two-
level system can be expressed in a matrix form as
H=ℏ [ Γ /2 Ω
Ω ω−Γ / 2 ]
Where ωℏ is the energy difference between the excited and the ground state, Ω is
the Rabi frequency, which induces oscillations between the two levels, and Γ is a
dissipation rate.
1. Show that the energies of the Eigen states of the Hamiltonian are given by
E1= ℏ
2 ¿ – Γ And E2= ℏ
2 ¿ – Γ
¿ the Hamilton ¿ we can find the eigen−energies as
Using the matrix given

9
( E1 )=1
2 ¿ +ω−Γ /2) + 1
2 √ ( Γ
2 −ω− Γ
2 )
2
+ 4 │ Ω│2
( E2 ) =1
2 ¿ +ω−Γ /2)−¿ 1
2 √ ( Γ
2 −ω− Γ
2 )
2
+ 4 │ Ω│2
E1= ℏ
2 (ω+ ¿ (4 Ω2+ω ¿1/ 2- Γ ¿
E2= ℏ
2 (ω−¿ (4 Ω2+ω ¿1/ 2- Γ ¿
Therefore E1= ℏ
2 ¿ –Γ ) and E2= ℏ
2 ¿–Γ)
2. In the previous question, how can you interpret the fact that the energies are
complex numbers?
They allowsustable frequencies ¿ be found ∈one run for one set of
operating conditions .
3. The Eigen states of the Hamiltonian can be expressed as
|ψ1 ⟩=c1|g ⟩ +c2∨e ⟩ , and|ψ2 ⟩ =d1| g ⟩ +d2∨ e ⟩ ,
Find the coefficients c1,c2, d1 and d2 in terms of the parameters of the system,
namely ω , Ω and Γ .
Hint: Remember that the elements of the basis are orthonormal ⟨ g │ e ⟩=0 ,
⟨ g │ g ⟩ = ⟨ e │e ⟩ =1 and that the states have to be normalized.
│ψ± ⟩ =cos ( θ
2 )│ exp (-iφ /2 )│Φ 1>+sin ¿exp (iφ /2 )│Φ 2>
¿ (-iφ / 2 )│Φ 1>+cos ¿ (iφ /2 )│Φ 2>
Tan θ = 2│ Ω│ / ( Γ
2 −ω−Γ /2 ¿

10
Where tan θ =2 (
Ω
Γ
2 −(ω− Γ
2 )), and Ω=│Ω │ ei φ
4. Show that if α , β ∈C such that │ α │2 +│ β │2 = 1, the state
ψ ( x ) = α e
−i E1 t
ℏ | ψ1 ⟩ + β e
−i E2 t
ℏ |ψ2 ⟩
│ α │2 +│ β │2 = 1
ψ ( x ) =│α │2 wℏ ( ψ1 ) +│ β │2 wℏ ( ψ2 )
where w=e
−iEt
ℏ
ψ ( x ) = α e
−i E1 t
ℏ | ψ1 ⟩ + β e
−i E2 t
ℏ |ψ2 ⟩
Is a solution to the time-dependent Schrödinger equation?
ψ ( x ) =U ( ψ ) is atime dependent of ψ1 ⟩ where U isthe time evolution operator
5. Using the state of the previous question, show that the probability to find the two
level system in its ground state is
Pg ( t )=│ ⟨ g │ψ ( t ) ⟩ │2=¿+α β+¿ c1 d 1
+¿ ei (ω2−ω1 )t
¿ ¿)e− Γt
And the probability to find it in its excited state is given by
Pe ( t ) =│ ⟨ ϵ │ψ ( t ) ⟩ │2 =¿+α β+¿ c2 d 2
+¿ ei ( ω2−ω1 ) t
¿ ¿)e− Γt
Where ωi = Ei /ℏ for i = 1, 2.
Are the probabilities conserved (is their sum equal to 1 at all times)? Discuss what
happens.
ψ ( x ) = α e
−i E1 t
ℏ | ψ1 ⟩ + β e
−i E2 t
ℏ |ψ2 ⟩
Suppose the original stste of the systemψ ( x , 0 ) =ϕ1( x )

11
Then C−¿=cos θ∧C+¿=−sin θ¿ ¿
ψ ( x ) =¿ ¿ +sin2 θ e−i E+ ¿t /ℏ¿]ϕ 1+sin θ cos θ ¿
Therefore Pg ( t ) =¿+α β+¿ c1 d 1
+¿ ei ( ω2−ω1 ) t
¿ ¿)e− Γt
¿ Pe ( t )=¿+α β+¿ c2 d 2
+¿ ei (ω2−ω1 )t
¿ ¿)e− Γt
6. Solve the time-dependent Schrödinger equation to show that if the two-level
system is initially in its excited state, that is |ϕ (0) ⟩ = | e ⟩, then at later times the
state is given by | ϕ (t) ⟩ = cg(t ) | g ⟩ + ce(t ) |e ⟩where the coefficients are given by
Cg (t) = −2 iΩ
√4 Ω2 +ω2 sin( √4 Ω2+ ω2 Γ
2 ) ε− Γt e−iωt /2
Ce (t) =¿
ψ ( x ) =¿ ¿ +sin2 θ e−i E+ ¿t /ℏ¿]ϕ 1+sin θ cos θ ¿
Pe ( t ) =4 sin2 θ cos2 θ sin2 √ ∆2 +V 2 t/ℏ
Pe ( t ) = 1
2
V 2
∆2+V 2
−1
2
V 2
∆2 +V 2 Cos 2√ ∆2 +V 2 t/ℏ
Pg ( t )= 1
2
2 ∆2+V 2
∆2 +V 2
+ 1
2
V 2
∆2 +V 2 cos2√ ∆2 +V 2 t/ℏ
Therefore
Cg (t) = −2 iΩ
√4 Ω2 +ω2 sin( √4 Ω2+ ω2 Γ
2 ) ε− Γt e−iωt /2
Ce (t) =¿

12
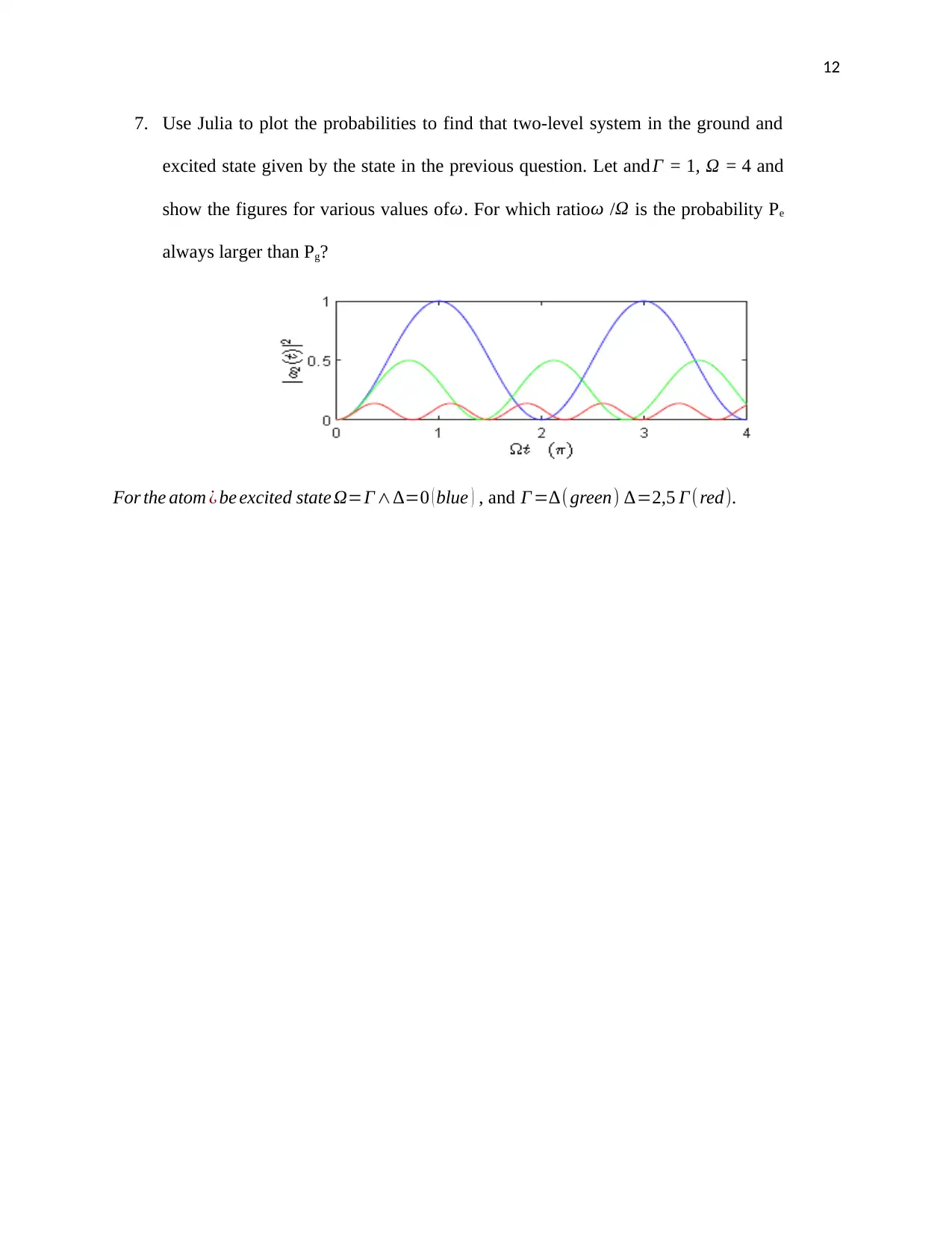
7. Use Julia to plot the probabilities to find that two-level system in the ground and
excited state given by the state in the previous question. Let and Γ = 1, Ω = 4 and
show the figures for various values ofω. For which ratioω /Ω is the probability Pe
always larger than Pg?
For the atom ¿ be excited state Ω=Γ ∧∆=0 ( blue ) , and Γ =∆( green) ∆=2,5 Γ (red).