SIT718 Real World Analytics Assignment 1: Linear Programming Solutions
VerifiedAdded on 2022/10/03
|9
|1996
|46
Homework Assignment
AI Summary
This assignment solution covers various problems in real-world analytics. It includes formulating and solving a linear programming problem to minimize costs in a food factory, determining the optimal mix of ingredients for beverage production using Desmos. It also involves solving a product mix problem using R to maximize profit, analyzing a two-player zero-sum game to determine optimal strategies using linear programming, and finding the Nash equilibrium in a pricing game between two companies. The solutions use tools like Desmos and R, and concepts from game theory and linear optimization are applied. Desklib provides access to similar solved assignments and study resources for students.

Analytics Assignment 1
Real World Analytics
by[Name]
Course
Professor’s Name
Institution
Location of Institution
Date
Real World Analytics
by[Name]
Course
Professor’s Name
Institution
Location of Institution
Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Analytics Assignment 2
Real World Analytics: Assignment 4
Question 1
(a) The problem is described in a way that a system of linear equations can be formed.
There is an objective in the problem (minimize costs). A direct link between the
objective and the constraints can be represented by a linear relationship. Next, the
restrictions on the mount of product A or B than can be used in making the beverage
is provided in the question (Morris 2012). The problem satisfies the non-negativity
assumption of linear programming. From the problem negative units of the product A
and B does not exists.
(b) Suppose the food factory use x = liters of product A and y liters of product B in
producing the beverage. This implies that the total volume of beverage produced is (x
+ y) liters.
C = 5x + 7y.
In addition to the cost the restrictions are presented as follows:
Orange x + 2
3 y ≥ 75
Mango x + 3
2 y ≥ 125
Lime x + 8
3 y ≤200 , x ≥ 0 and y≥ 0.
In mathematical terms, the problem is to:
Min C = 5x + 7y.
Subject to:
x + 2
3 y ≥ 75, x + 3
2 y ≥ 125, x + 8
3 y ≤200, x ≥ 0 and y ≥ 0.
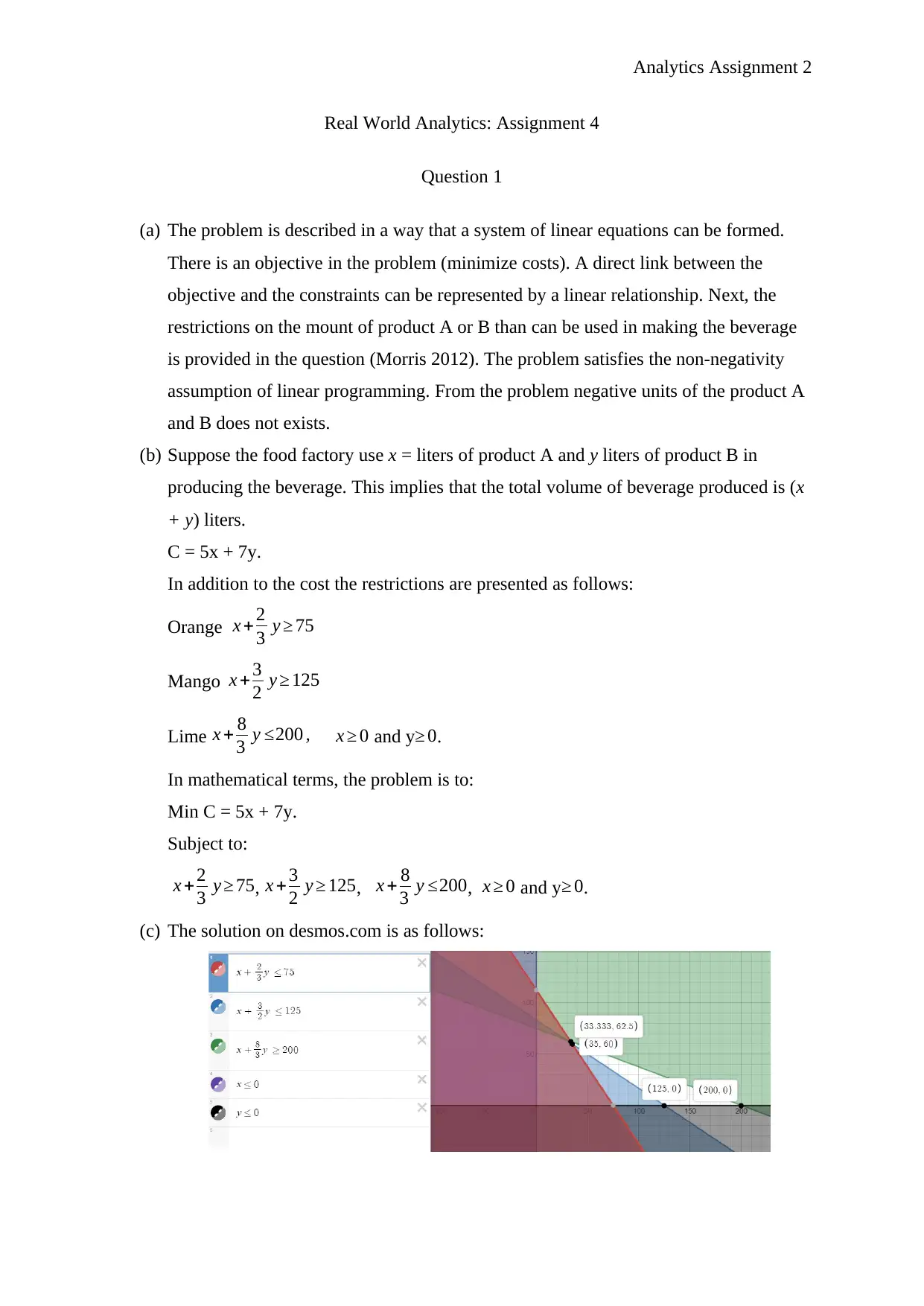
(c) The solution on desmos.com is as follows:
Real World Analytics: Assignment 4
Question 1
(a) The problem is described in a way that a system of linear equations can be formed.
There is an objective in the problem (minimize costs). A direct link between the
objective and the constraints can be represented by a linear relationship. Next, the
restrictions on the mount of product A or B than can be used in making the beverage
is provided in the question (Morris 2012). The problem satisfies the non-negativity
assumption of linear programming. From the problem negative units of the product A
and B does not exists.
(b) Suppose the food factory use x = liters of product A and y liters of product B in
producing the beverage. This implies that the total volume of beverage produced is (x
+ y) liters.
C = 5x + 7y.
In addition to the cost the restrictions are presented as follows:
Orange x + 2
3 y ≥ 75
Mango x + 3
2 y ≥ 125
Lime x + 8
3 y ≤200 , x ≥ 0 and y≥ 0.
In mathematical terms, the problem is to:
Min C = 5x + 7y.
Subject to:
x + 2
3 y ≥ 75, x + 3
2 y ≥ 125, x + 8
3 y ≤200, x ≥ 0 and y ≥ 0.
(c) The solution on desmos.com is as follows:

Analytics Assignment 3
From the values at the corner points gives a minimum total cost of 595 at point (35,
60). Therefore, the factory should use 35 liters of product A and 60 liters of product B
to produce 95 liters of the beaverage.
(d) Increasing the liters of A by one unit shift optimal solution to (33.33, 62.5). This
means that the price should be less than one. After tring values between 5 to 5.9 we
realise the values that A can take without chnaging the position of the optimal
solution is between 5 and 5.85 liters of product A.
Question 2
(a) Using the hint provided in the question wee have: xij ≥ 0 as the decision variable
interprated as the amount in tons of products j where
j ϵ { 1=Spring;2=Autumn ; 3=Winter } produced from materials i where
i ϵ {C=Cotton ,W =Wool , S=Silk } . Further, the proportion of a particular type of
material in a particular type of product is given by the formula ( i.e xc1
xc1 + xw 1+ xs 1
proportion of cotton in Spring).
Now, define profit as the difference between total cost and the total revenue:
Profit = Cost – Revenue, where Cost is the sum of production cost and purcahse
cost. Finally, Revenue is the product of sales price and deamnd.
Using the information provided we have:
Revenue=60 xc1 +60 xw 1+60 xs 1 +55 xc2 +55 xw 2+55 xs 2 +60 xc3 +60 xw 3+60 x s3
Production cost=5 ( xc 1+ xw1 +xs 1 ) +4 ( xc2 +xw 2+ xs 2 )+ 5 ( xc3 + xw 3+ xs 3 )
Purchase cost=30 xc1 + 45 xw 1 +50 xs 1+30 xc 2+ 45 xw 2+50 xs 2 +30 xc3 + 45 xw 3 +50 xs 3
Cost =35 xc 1 +50 xw1 +55 xs 1+ 34 xc2 + 49 xw 2 +54 xs 2 +35 xc3 +50 xw3 +55 xs 3
Profit=25 xc1 +10 xw 1+5 xs 1 +21 xc 2 +6 xw 2+x s2 +25 xc 3+10 xw 3 +5 xs 3
Thus problem is to
Max Profit=25 xc1 +10 xw 1+5 xs 1 +21 xc 2 +6 xw 2+ x s2 +25 xc 3+10 xw 3 +5 xs 3
Subject to:
( xc 1+xw 1 + xs 1 ≤ 4500 ) , ( xc 2+ xw 2 + xs 2 ≤ 3000 ), ( xc 3+ xw3 + xs 3 ≤3500 ),
( xc 1−xw 1−xs 1 ≥ 0 ), ( 3 xc1 −7 xw1 +3 xs 1 ≤ 0 ), ( xc 1+xw 1−4 xs 1 ≤ 0 ),
( xc 2−xw 2−xs 2 ≥ 0 ), ( 2 xc2−3 xw 2 +2 xs 2 ≤ 0 ), ( xc 2+xw 2−9 x s2 ≤ 0 ),
( 3 xc3 −2 xw 3−2 xs 3 ≥0 ), ( xc 3−xw 3+ xs 3 ≤ 0 ), ( xc 3+ xw3 −9 xs 3 ≤ 0 ),
xc 1 ≥ 0 , xc 2 ≥ 0 , xc3 ≥ 0 , xs 1 ≥ 0 , xs 2 ≥0 , xs 3 ≥0 , xw 1 ≥ 0 , xw2 ≥ 0 , xw 3 ≥0.
From the values at the corner points gives a minimum total cost of 595 at point (35,
60). Therefore, the factory should use 35 liters of product A and 60 liters of product B
to produce 95 liters of the beaverage.
(d) Increasing the liters of A by one unit shift optimal solution to (33.33, 62.5). This
means that the price should be less than one. After tring values between 5 to 5.9 we
realise the values that A can take without chnaging the position of the optimal
solution is between 5 and 5.85 liters of product A.
Question 2
(a) Using the hint provided in the question wee have: xij ≥ 0 as the decision variable
interprated as the amount in tons of products j where
j ϵ { 1=Spring;2=Autumn ; 3=Winter } produced from materials i where
i ϵ {C=Cotton ,W =Wool , S=Silk } . Further, the proportion of a particular type of
material in a particular type of product is given by the formula ( i.e xc1
xc1 + xw 1+ xs 1
proportion of cotton in Spring).
Now, define profit as the difference between total cost and the total revenue:
Profit = Cost – Revenue, where Cost is the sum of production cost and purcahse
cost. Finally, Revenue is the product of sales price and deamnd.
Using the information provided we have:
Revenue=60 xc1 +60 xw 1+60 xs 1 +55 xc2 +55 xw 2+55 xs 2 +60 xc3 +60 xw 3+60 x s3
Production cost=5 ( xc 1+ xw1 +xs 1 ) +4 ( xc2 +xw 2+ xs 2 )+ 5 ( xc3 + xw 3+ xs 3 )
Purchase cost=30 xc1 + 45 xw 1 +50 xs 1+30 xc 2+ 45 xw 2+50 xs 2 +30 xc3 + 45 xw 3 +50 xs 3
Cost =35 xc 1 +50 xw1 +55 xs 1+ 34 xc2 + 49 xw 2 +54 xs 2 +35 xc3 +50 xw3 +55 xs 3
Profit=25 xc1 +10 xw 1+5 xs 1 +21 xc 2 +6 xw 2+x s2 +25 xc 3+10 xw 3 +5 xs 3
Thus problem is to
Max Profit=25 xc1 +10 xw 1+5 xs 1 +21 xc 2 +6 xw 2+ x s2 +25 xc 3+10 xw 3 +5 xs 3
Subject to:
( xc 1+xw 1 + xs 1 ≤ 4500 ) , ( xc 2+ xw 2 + xs 2 ≤ 3000 ), ( xc 3+ xw3 + xs 3 ≤3500 ),
( xc 1−xw 1−xs 1 ≥ 0 ), ( 3 xc1 −7 xw1 +3 xs 1 ≤ 0 ), ( xc 1+xw 1−4 xs 1 ≤ 0 ),
( xc 2−xw 2−xs 2 ≥ 0 ), ( 2 xc2−3 xw 2 +2 xs 2 ≤ 0 ), ( xc 2+xw 2−9 x s2 ≤ 0 ),
( 3 xc3 −2 xw 3−2 xs 3 ≥0 ), ( xc 3−xw 3+ xs 3 ≤ 0 ), ( xc 3+ xw3 −9 xs 3 ≤ 0 ),
xc 1 ≥ 0 , xc 2 ≥ 0 , xc3 ≥ 0 , xs 1 ≥ 0 , xs 2 ≥0 , xs 3 ≥0 , xw 1 ≥ 0 , xw2 ≥ 0 , xw 3 ≥0.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Analytics Assignment 4
(b) The R-code is as follows:
require(lpSolve)
# Set the coefficients of the decision variables -> Profit
Profit <- c(25, 10, 5, 21, 6, 1, 25, 10, 5)
# Create constraint matrix A
A <- matrix(c(1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1,-1,-1,
0, 0, 0, 0, 0, 0, 3,-7, 3, 0, 0, 0, 0, 0, 0,
1, 1,-4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,-1,
-1,0, 0, 0, 0, 0, 0, 2,-3, 2, 0, 0, 0, 0, 0,
0, 1, 1,-9, 0, 0, 0, 0, 0, 0, 0, 0, 0,3,-2,-2,
0, 0, 0, 0, 0, 0, 1,-1, 1, 0, 0, 0, 0, 0, 0,
1, 1,-9, diag(9)), ncol = 9, byrow = T)
# Direction of constraints
CD <- c("<=", "<=", "<=", ">=", "<=", "<=",
">=", "<=", "<=", ">=", "<=", "<=",
">=", ">=", ">=", ">=", ">=", ">=",
">=", ">=", ">=")
# Right hand side for the constraints
B <- c(4500,3000,3500, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0)
# Find the optimal solution
optimum <- lp(direction="max",
objective.in = Profit,
const.mat = A,
const.dir = CD,
const.rhs = B,
compute.sens = T)
# Print status solutions
optimum$objval
optimum$solution
Thethe factory should use 2,250 tons of cotton, 1,350 tons of wool and 900 tons of
silk in producng Spring. For Autum, the factory should use 1,500 tons of cotton,
1,200 tons of wool and 300 tons of silk. Finally, for Winter, the factory should use
1,400 tons of cotton, 1,750 tons of wool and 350 tons of silk. This strategy will allow
the factory to make an optimal rofit of 167,500.
Question 3
(b) The R-code is as follows:
require(lpSolve)
# Set the coefficients of the decision variables -> Profit
Profit <- c(25, 10, 5, 21, 6, 1, 25, 10, 5)
# Create constraint matrix A
A <- matrix(c(1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1,-1,-1,
0, 0, 0, 0, 0, 0, 3,-7, 3, 0, 0, 0, 0, 0, 0,
1, 1,-4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,-1,
-1,0, 0, 0, 0, 0, 0, 2,-3, 2, 0, 0, 0, 0, 0,
0, 1, 1,-9, 0, 0, 0, 0, 0, 0, 0, 0, 0,3,-2,-2,
0, 0, 0, 0, 0, 0, 1,-1, 1, 0, 0, 0, 0, 0, 0,
1, 1,-9, diag(9)), ncol = 9, byrow = T)
# Direction of constraints
CD <- c("<=", "<=", "<=", ">=", "<=", "<=",
">=", "<=", "<=", ">=", "<=", "<=",
">=", ">=", ">=", ">=", ">=", ">=",
">=", ">=", ">=")
# Right hand side for the constraints
B <- c(4500,3000,3500, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0)
# Find the optimal solution
optimum <- lp(direction="max",
objective.in = Profit,
const.mat = A,
const.dir = CD,
const.rhs = B,
compute.sens = T)
# Print status solutions
optimum$objval
optimum$solution
Thethe factory should use 2,250 tons of cotton, 1,350 tons of wool and 900 tons of
silk in producng Spring. For Autum, the factory should use 1,500 tons of cotton,
1,200 tons of wool and 300 tons of silk. Finally, for Winter, the factory should use
1,400 tons of cotton, 1,750 tons of wool and 350 tons of silk. This strategy will allow
the factory to make an optimal rofit of 167,500.
Question 3
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Analytics Assignment 5
(a) The game is structured in such a away that there are two players. Indicating that the
two-player part is satisfied. Next, at each stage of the play either Hellen wins or David
wins. The amount won is equal to the amount losts; therefore the sum of the payoff of
the two players is zero at every play (Karlin and Peres 2016). The conditions for a
two players zero sum games are satisfied by the problem decribed in the case game
between Hellen and David.
(b) The payoff matrix B
David
Hellen
|−5
0
0
−5 0 0
−5 −5 0
0 −5 −10
0 −5 −5
−5 −5 0
−5 0 0
0
0
−5
0 −5 −10
−5 −5 0
−5 0 0
−5 0 0
−5 −5 0
0 −5 −5
|(c) According to Karlin and Peres (2016), “saddle point refers to a value of the game
between two player which is a maximum with respect to row player and a mnimax
with respect to the column.” In a payoff matrix saddle point exists if the row minimax
is equal to the column maximin. That is the amount minimum amount that the row
players is able to pay if he/she choses any strategy. In the payoff matrix (b) there is no
saddle point since the minimax = 5 is not equal the maximin = 0.
(d) Suppose David pick strategy i with probability pi and Hellen pick strategy j with
probability q j.
Also, let p= ( p1 , p2 ,… , p7 )T and q= ( q1 ,q2 ,.. , q6 )T .
Probability adds to 1 implying that
p7=1− ( p1 +p2+ p3+ p4 + p5 + p6 ) and q6=1− ( q1 +q2+ q3 +q4 +q5 )
Let the amount won by any player be represented by a scalar a which is the payoff of
the game.
The LP for David is to max a
Subject to:
−a e1 +B p ≥ 0, 0 ≤ pi ≤ 1 and ∑
i=1
7
pi =1
Where: e1 vector of 1’s.
The LP for Hellen is min a
Subject to:
(a) The game is structured in such a away that there are two players. Indicating that the
two-player part is satisfied. Next, at each stage of the play either Hellen wins or David
wins. The amount won is equal to the amount losts; therefore the sum of the payoff of
the two players is zero at every play (Karlin and Peres 2016). The conditions for a
two players zero sum games are satisfied by the problem decribed in the case game
between Hellen and David.
(b) The payoff matrix B
David
Hellen
|−5
0
0
−5 0 0
−5 −5 0
0 −5 −10
0 −5 −5
−5 −5 0
−5 0 0
0
0
−5
0 −5 −10
−5 −5 0
−5 0 0
−5 0 0
−5 −5 0
0 −5 −5
|(c) According to Karlin and Peres (2016), “saddle point refers to a value of the game
between two player which is a maximum with respect to row player and a mnimax
with respect to the column.” In a payoff matrix saddle point exists if the row minimax
is equal to the column maximin. That is the amount minimum amount that the row
players is able to pay if he/she choses any strategy. In the payoff matrix (b) there is no
saddle point since the minimax = 5 is not equal the maximin = 0.
(d) Suppose David pick strategy i with probability pi and Hellen pick strategy j with
probability q j.
Also, let p= ( p1 , p2 ,… , p7 )T and q= ( q1 ,q2 ,.. , q6 )T .
Probability adds to 1 implying that
p7=1− ( p1 +p2+ p3+ p4 + p5 + p6 ) and q6=1− ( q1 +q2+ q3 +q4 +q5 )
Let the amount won by any player be represented by a scalar a which is the payoff of
the game.
The LP for David is to max a
Subject to:
−a e1 +B p ≥ 0, 0 ≤ pi ≤ 1 and ∑
i=1
7
pi =1
Where: e1 vector of 1’s.
The LP for Hellen is min a
Subject to:

Analytics Assignment 6
−a e2 +BT q ≥ 0, 0 ≤ qi ≤1, and ∑
i=1
6
qi=1
Where e2 vector of 1’s.
(e) The LP for David is expanded in matrix form as follows: We exclude inequalities that
are linearly dependent.
a=−a e1 +B p=¿ ( −1 0 0 5 5 5 0 −5
−1 0 −5 −5 0 −5 −5 0
−1 0 0 −5 −10 −5 0 0 )
0 ≤
( 0 1 0
0 0 1
0 0 0
0 0 0
0 0 0
1 0 0
0 0
0 0
0 0
0 0 0
0 0 0
0 0 0
0 1 0
0 0 1
0 0 0
0 0
0 0
1 0
0 −1 −1 −1 −1 −1 −1 1
) ≤1
The R-code for the solution is
a <- matrix(c(-1, 0, 0, 5, 5, 5, 0,-5,
-1, 0,-5,-5, 0,-5,-5, 0,
-1, 0, 0,-5,-10,-5, 0,0), ncol = 8, byrow = T)
aa <-rbind(cbind(cbind(matrix(c(0, 0, 0,
0, 0, 0), nrow=6,
byrow=T),diag(6)),
matrix(c(0, 0, 0,
0, 0, 0), nrow=6, byrow=T)),
matrix(c(0,-1,-1,-1,
-1,-1,-1,1),ncol = 8))
# The objective function
S <- c(1, 0, 0, 0,
0, 0, 0, 0)
# Constraint matrix
CM <- rbind(a,aa)
CM <- rbind(CM, aa)
# Constraints directions
cd <- c(">=", ">=", ">=", ">=", ">=", ">=",
">=", ">=", ">=", ">=",
"<=", "<=", "<=", "<=",
"<=", "<=", "<=")
## constraint right hand side value
CRH <- c(0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1)
−a e2 +BT q ≥ 0, 0 ≤ qi ≤1, and ∑
i=1
6
qi=1
Where e2 vector of 1’s.
(e) The LP for David is expanded in matrix form as follows: We exclude inequalities that
are linearly dependent.
a=−a e1 +B p=¿ ( −1 0 0 5 5 5 0 −5
−1 0 −5 −5 0 −5 −5 0
−1 0 0 −5 −10 −5 0 0 )
0 ≤
( 0 1 0
0 0 1
0 0 0
0 0 0
0 0 0
1 0 0
0 0
0 0
0 0
0 0 0
0 0 0
0 0 0
0 1 0
0 0 1
0 0 0
0 0
0 0
1 0
0 −1 −1 −1 −1 −1 −1 1
) ≤1
The R-code for the solution is
a <- matrix(c(-1, 0, 0, 5, 5, 5, 0,-5,
-1, 0,-5,-5, 0,-5,-5, 0,
-1, 0, 0,-5,-10,-5, 0,0), ncol = 8, byrow = T)
aa <-rbind(cbind(cbind(matrix(c(0, 0, 0,
0, 0, 0), nrow=6,
byrow=T),diag(6)),
matrix(c(0, 0, 0,
0, 0, 0), nrow=6, byrow=T)),
matrix(c(0,-1,-1,-1,
-1,-1,-1,1),ncol = 8))
# The objective function
S <- c(1, 0, 0, 0,
0, 0, 0, 0)
# Constraint matrix
CM <- rbind(a,aa)
CM <- rbind(CM, aa)
# Constraints directions
cd <- c(">=", ">=", ">=", ">=", ">=", ">=",
">=", ">=", ">=", ">=",
"<=", "<=", "<=", "<=",
"<=", "<=", "<=")
## constraint right hand side value
CRH <- c(0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Analytics Assignment 7
# Find the optimal solution
optimum1 <- lp(direction="max",
objective.in = S,
const.mat = CM,
const.dir = cd,
const.rhs = CRH,
compute.sens = T)
# Print status solutions
optimum1$objval
optimum1$solution
(f) This game is biased since David cannot have a wining strategy because he has less
chips.
Question 4
(a) Le us define ProfitI as the profit for company i for i∈ {1=company 1 , 2=company 2 }.
We have been given the following information in the problem:
Q1=200−P1− ( P1−P ) , Q2=200−P2− ( P2 −P )and P= P1 +P2
2 .
Now we simplify these equations into the following:
Q1=200−1.5 P1+0.5 P2 and Q2=200+ 0.5 P1 −1.5 P2
The profit from sale of the cellphones under different price strategies are as follows: :
Strategy P1=70 P2=70
Profitcompany 1= ( 200−1.5 ( 70 )+0.5 ( 70 ) ) x 55=7,150
Profitcompany 2= ( 200+0.5 ( 70 ) −1.5 ( 70 ) ) x 55=7,150
Strategy P1=70 P2=80
Profitcompany 1= ( 200−1.5 ( 70 ) + 0.5 ( 80 ) ) x 55=7,425
Profitcompany 2= ( 200+ 0.5 ( 70 ) −1.5 ( 80 ) ) x 65=7,475
Strategy P1=70 P2=90
Profitcompany 1= ( 200−1.5 ( 70 )+ 0.5 ( 90 ) ) x 55=7,700
Profitcompany 2= ( 200+0.5 ( 70 ) −1.5 ( 90 ) ) x 75=7,500
Strategy P1=80 P2=70
Profitcompany 1= ( 200−1.5 ( 80 ) +0.5 ( 70 ) ) x 65=7,475
# Find the optimal solution
optimum1 <- lp(direction="max",
objective.in = S,
const.mat = CM,
const.dir = cd,
const.rhs = CRH,
compute.sens = T)
# Print status solutions
optimum1$objval
optimum1$solution
(f) This game is biased since David cannot have a wining strategy because he has less
chips.
Question 4
(a) Le us define ProfitI as the profit for company i for i∈ {1=company 1 , 2=company 2 }.
We have been given the following information in the problem:
Q1=200−P1− ( P1−P ) , Q2=200−P2− ( P2 −P )and P= P1 +P2
2 .
Now we simplify these equations into the following:
Q1=200−1.5 P1+0.5 P2 and Q2=200+ 0.5 P1 −1.5 P2
The profit from sale of the cellphones under different price strategies are as follows: :
Strategy P1=70 P2=70
Profitcompany 1= ( 200−1.5 ( 70 )+0.5 ( 70 ) ) x 55=7,150
Profitcompany 2= ( 200+0.5 ( 70 ) −1.5 ( 70 ) ) x 55=7,150
Strategy P1=70 P2=80
Profitcompany 1= ( 200−1.5 ( 70 ) + 0.5 ( 80 ) ) x 55=7,425
Profitcompany 2= ( 200+ 0.5 ( 70 ) −1.5 ( 80 ) ) x 65=7,475
Strategy P1=70 P2=90
Profitcompany 1= ( 200−1.5 ( 70 )+ 0.5 ( 90 ) ) x 55=7,700
Profitcompany 2= ( 200+0.5 ( 70 ) −1.5 ( 90 ) ) x 75=7,500
Strategy P1=80 P2=70
Profitcompany 1= ( 200−1.5 ( 80 ) +0.5 ( 70 ) ) x 65=7,475
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Analytics Assignment 8
Profitcompany 2= ( 200+ 0.5 ( 80 )−1.5 ( 70 ) ) x 55=7,425
Company 1
Company 2
|
(7,150 ,7,150) (7,425 ,7,475) (7,700 , 7,500)
(7,475 ,7,425) (7,800 ,7,800) (8,125 , 7,875)
(7,500 ,7,700) (7,875 , 8,125) (8,250 , 8,250)|
(b) The process involves elimination of dominant strategies to arrive the nash
equilibrium(Morris 2012).
P1=90 dominates P2=70 for company 2 so we elimiante the the first column.
P1=80 is dominated by both P2=80 and P2=80 for company 1 so we elimiante the
the second row. Next, P1=90 dominates P2=90 for company 2 so we elimiante the
last column. Therefore, the best strategy (Nash equilibrium) for the two companies is
at P1=90∧¿ P2=80.
The profits are 7,875 and 8,125 for company 1 and 2 respectively.
(c) The changes in cost does not affect the strategy since the change involves a constnat
which will affect every strategy. Therefore, the optimal strategy will still be (90, 80).
Profitcompany 2= ( 200+ 0.5 ( 80 )−1.5 ( 70 ) ) x 55=7,425
Company 1
Company 2
|
(7,150 ,7,150) (7,425 ,7,475) (7,700 , 7,500)
(7,475 ,7,425) (7,800 ,7,800) (8,125 , 7,875)
(7,500 ,7,700) (7,875 , 8,125) (8,250 , 8,250)|
(b) The process involves elimination of dominant strategies to arrive the nash
equilibrium(Morris 2012).
P1=90 dominates P2=70 for company 2 so we elimiante the the first column.
P1=80 is dominated by both P2=80 and P2=80 for company 1 so we elimiante the
the second row. Next, P1=90 dominates P2=90 for company 2 so we elimiante the
last column. Therefore, the best strategy (Nash equilibrium) for the two companies is
at P1=90∧¿ P2=80.
The profits are 7,875 and 8,125 for company 1 and 2 respectively.
(c) The changes in cost does not affect the strategy since the change involves a constnat
which will affect every strategy. Therefore, the optimal strategy will still be (90, 80).

Analytics Assignment 9
References
Desmos Graphing Calculator. (2019). Desmos graph. [online] Available at:
https://www.desmos.com/calculator [Accessed 28 Sep. 2019].
Karlin, A.R. and Peres, Y., 2017. Game theory, alive (Vol. 101). American Mathematical
Soc..
Morris, P., 2012. Introduction to game theory. Springer Science & Business Media.
References
Desmos Graphing Calculator. (2019). Desmos graph. [online] Available at:
https://www.desmos.com/calculator [Accessed 28 Sep. 2019].
Karlin, A.R. and Peres, Y., 2017. Game theory, alive (Vol. 101). American Mathematical
Soc..
Morris, P., 2012. Introduction to game theory. Springer Science & Business Media.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



![Course Name: Real World Analytics Assignment Solution - [Date]](/_next/image/?url=https%3A%2F%2Fdesklib.com%2Fmedia%2Fimages%2Fjs%2F7cd677b2bca5453d86bfbb121190a9b2.jpg&w=256&q=75)

