Exploring Tent Map Dynamics, Cellular Automata, and Graph Girth

This assignment delves into the analysis of dynamical systems, cellular automata, and graph theory. The first part focuses on the tent map, exploring its fixed points, stability, and the presence of 2-cycles, with a bifurcation diagram illustrating its behavior. The assignment then shifts to cellular automata, examining Rule 90 and the B25/S4 rule, including replicators and photons, and their interactions. Finally, it presents graph theory problems, specifically concerning the girth of graphs with a specific relationship between edges and vertices, requiring the explanation of cycle existence and the construction of graphs with edge-disjoint cycles and maximal girth. The assignment covers a wide array of AI concepts.

Recurrence, Relations (RR) and Cellular Automata (CA)
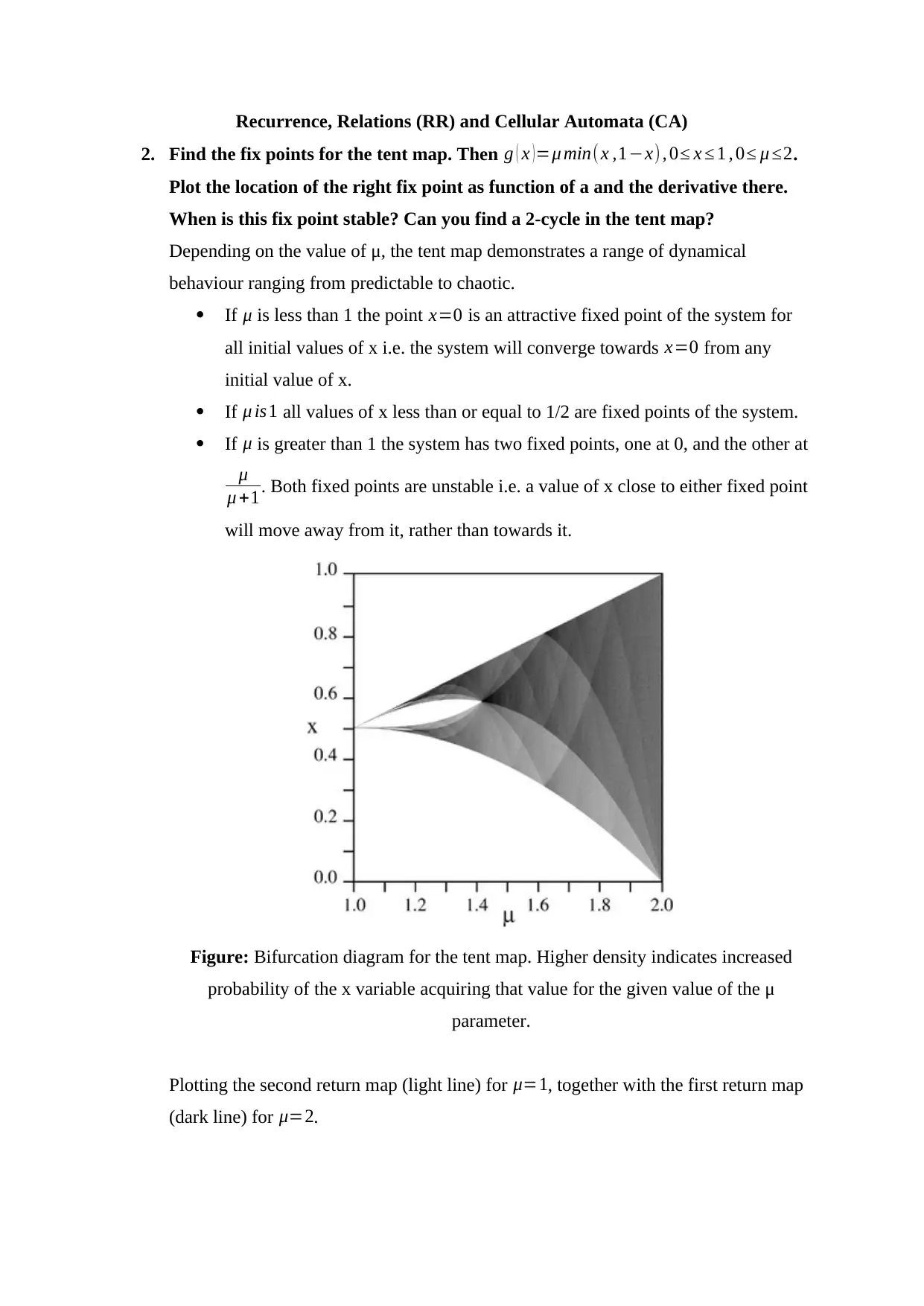
2. Find the fix points for the tent map. Then g ( x ) =μ min( x ,1−x), 0≤ x ≤ 1 , 0≤ μ ≤2.
Plot the location of the right fix point as function of a and the derivative there.
When is this fix point stable? Can you find a 2-cycle in the tent map?
Depending on the value of μ, the tent map demonstrates a range of dynamical
behaviour ranging from predictable to chaotic.
 If μ is less than 1 the point x=0 is an attractive fixed point of the system for
all initial values of x i.e. the system will converge towards x=0 from any
initial value of x.
 If μ is1 all values of x less than or equal to 1/2 are fixed points of the system.
 If μ is greater than 1 the system has two fixed points, one at 0, and the other at
μ
μ +1. Both fixed points are unstable i.e. a value of x close to either fixed point
will move away from it, rather than towards it.
Figure: Bifurcation diagram for the tent map. Higher density indicates increased
probability of the x variable acquiring that value for the given value of the μ
parameter.
Plotting the second return map (light line) for μ=1, together with the first return map
(dark line) for μ=2.

Figure: Tent Map
The 2-cycle is shown by the dashed square.
From the dashed square, we see one point, x, of the 2-cycle is less than 1/2, while the
other, y, is greater than 1/2. Then using equation above
xn+1=μ xn if xn ≤ 0.5
xn+1=μ (1−xn )if xn >0.5
we see y=μ × x andx=μ ×(1− y ). Combining these, x=μ(1−μx). Solving for x gives
x= μ
1+μ2 . Then y=μx= μ2
1+μ2 .
3. Consider the following 1D CA: A cell is black in next generation if and only if
either of its neighbors, but not both, was black on the step before. What is the
rule number? Do 5 iterations using one black cell as seed.
This is Rule 90 as shown in the Image below.
Figure: Rule 190 1D-CA
Let assume the initial state at time t=0 is given as:

t=0 ⇒ 0 , 1 , 0 , 0 ,0
Then,
t=1 ⇒0 , 0 ,1 , 0 , 0
t=2 ⇒ 0 , 1 ,0 , 1 , 0
t=3 ⇒ 0 , 0 , 0 , 0 , 0
t=4 ⇒ 0 , 0 , 0 , 0 ,0
t=5 ⇒ 0 , 0 , 0 , 0 , 0
4. Consider the rule B25/S4. B denotes birth and S survival. Game of Life is
B3/S23. What is the rule number for B25/S4? Do 3 iterations for the first one.
Note that we have up-down symmetry. It is called a replicator. Do one iteration
for the second one. It is called a photon.
B25/S4
Rule B25/S4 like in B2/S13 copies itself every three generations on a one-
dimensional 3-unit grid. However, the replicator is asymmetric. This rule supports a
small self-replicating pattern which, when combined with a small glider pattern,
causes the glider to bounce back and forth in a pseudorandom walk.
B25/S4 contains a small period-3 replicator, and (like most B2 rules without B3/S1)
supports small photons, spaceships that move at speed c. If a photon and a replicator
are aligned on the same axis, their interaction will destroy that copy of the replicator
and emit an oppositely-oriented photon. Placing a photon between two appropriately
spaced replicators (shown in the image below) leads to a pattern in which the photon
repeatedly bounces back and forth between copies of the replicators on both sides,
following a pseudorandom walk in which the typical distance of the photon from its
starting point at step n appears to be proportional to √n.
Figure: A spaceship sandwiched between two replicators in B25/S4 leads to
pseudorandom behavior
B3/S23
The rules of the original Life are:

1. BIRTH: a new cell arises in a blank square if and only if it is surrounded by exactly
other three alive cells. No more than three, no less.
2. SURVIVAL: a cell survives if and only if it is surrounded by others two or three alive
cells. No more, no less.
3. DEATH: if a cell is surrounded by less than two (isolation) and more than three cells
(overpopulation) it dies.
Figure: 4 iterations of B3/S23
6. The girth of a graph G is the number of edges of the shortest cycle it is possible
to find in G and it is denoted g (G). Let, from now on, the graphs G have e = v +
1 For such graphs with v ≥ 4 it is possible to show that
The floor function [x] gives the largest integer ≤ x.
a) Explain why in this type of graphs, there must be at least two cycles. Draw a
case where the cycles are edge disjoint for v = 7 and e = 8.
Since the number of edges are more than the number of vertices, we will have
atleast 2 cycles in this type of graphs.
Figure: Graph with v = 7 and e = 8 and edge-disjoint cycles
b) If the two cycles are edge disjoint what is the maximum girth in a graph with
e = v+ 1?
The maximal girth of the graph under these conditions is equal to 4.
c) Draw a graph with maximal girth for v = 7 and e = 8

Figure: Graph with v = 7 and e = 8 and edge-disjoint cycles and maximum girth
of 4