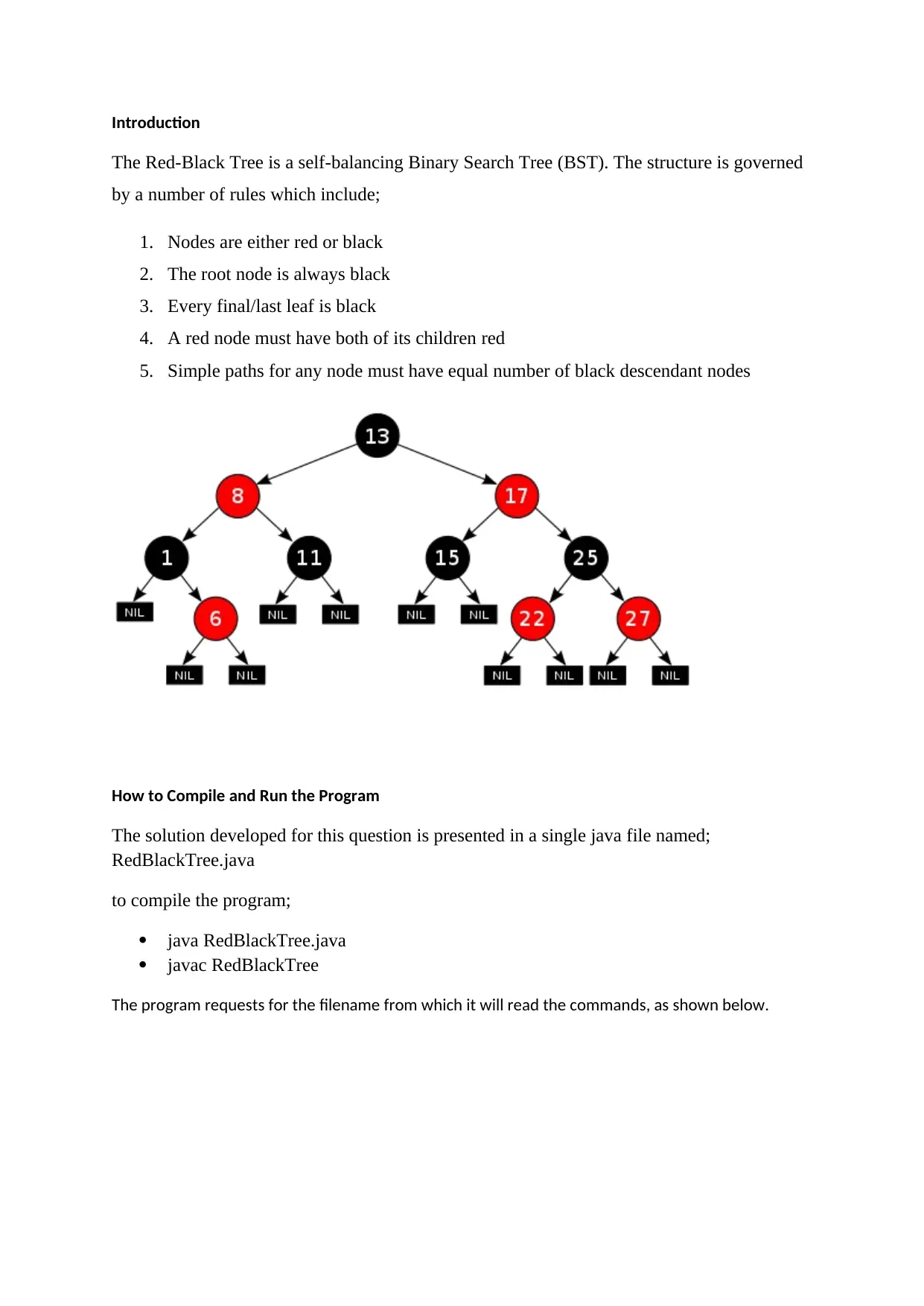
Red-Black Tree: Implementation and Operations in Java Programming

This assignment presents a complete Java implementation of a Red-Black Tree, a self-balancing binary search tree. The code includes the `RBNode` class to represent nodes with color (red or black), data, and links to parent, left, and right children. The implementation covers essential operations such as insertion (`insert`), deletion (`delete`), and search (`search`). The `insert` function incorporates the `fixTree` method to maintain the Red-Black Tree properties after insertion, ensuring self-balancing through rotations and color adjustments. The `delete` function includes `transplant` and `deleteFixup` methods for handling node deletion while preserving the tree's structure and balance. Additional methods like `rotateLeft`, `rotateRight`, and `treeMinimum` are used to maintain the Red-Black Tree properties. The `run` method handles user input from a file, allowing the user to specify operations (insert or delete) on the tree. The `main` method instantiates the `RedBlackTree` class and initiates the program's execution by calling the `run` method. The code is designed to compile and run, demonstrating the functionality of a Red-Black Tree data structure. This solution is provided on Desklib, a platform that offers AI-based study tools and resources for students.

Introduction
The Red-Black Tree is a self-balancing Binary Search Tree (BST). The structure is governed
by a number of rules which include;
1. Nodes are either red or black
2. The root node is always black
3. Every final/last leaf is black
4. A red node must have both of its children red
5. Simple paths for any node must have equal number of black descendant nodes
How to Compile and Run the Program
The solution developed for this question is presented in a single java file named;
RedBlackTree.java
to compile the program;
 java RedBlackTree.java
 javac RedBlackTree
The program requests for the filename from which it will read the commands, as shown below.

SOURCE CODE
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.Scanner;
public class RedBlackTree {
//The colors will be represented by 0 and 1
private final int RED = 0;
private final int BLACK = 1;
private final RBNode nil = new RBNode(-1);
private RBNode root = nil;
/*
We use a private inner class
to define the NODE
*/
private class RBNode {
int data = -1;
int color = BLACK;
RBNode left = nil;
RBNode right = nil;
RBNode parent = nil;

public RBNode(int key) {
this.data = key;
}
/**
* Constructor
*/
public RBNode(int key, RBNode parent, RBNode left, RBNode right, char color) {
this.data = key;
this.parent = parent;
this.left = left;
this.right = right;
this.color = color;
}
void setColor(char color) {
this.color = color;
}
}
/**
* This function prints out the Tree
* inorder
* @param node
*/
void printInorder(RBNode node) {

if (node == nil) {
return;
}
printInorder(node.left);
//Uncommenting this line will provide a detailed printout of the tree
//System.out.print(((node.color == RED) ? "Color: Red " : "Color: Black ") + "Key: " + node.key + "
Parent: " + node.parent.key + "\n");
System.out.print(node.data + " ");
printInorder(node.right);
}
/**
* This function searches a Node
* @param nodeToSearch
* @param rootNode
* @return
*/
private RBNode searchNode(RBNode nodeToSearch, RBNode rootNode) {
if (root == nil) {
return null;
}
if (nodeToSearch.data < rootNode.data) {
if (rootNode.left != nil) {
return searchNode(nodeToSearch, rootNode.left);
}
} else if (nodeToSearch.data > rootNode.data) {
if (rootNode.right != nil) {

return searchNode(nodeToSearch, rootNode.right);
}
} else if (nodeToSearch.data == rootNode.data) {
return rootNode;
}
return null;
}
/**
* Function to insert a node into a tree
* @param node
*/
private void insert(RBNode node) {
RBNode temp = root;
if (root == nil) {
root = node;
node.color = BLACK;
node.parent = nil;
} else {
node.color = RED;
while (true) {
if (node.data < temp.data) {
if (temp.left == nil) {
temp.left = node;
node.parent = temp;
break;
} else {

temp = temp.left;
}
} else if (node.data >= temp.data) {
if (temp.right == nil) {
temp.right = node;
node.parent = temp;
break;
} else {
temp = temp.right;
}
}
}
fixTree(node);
}
}
/**
* This function fixes the tree.
* It takes the newly inserted Node as
* an argument
* @param node
*/
private void fixTree(RBNode node) {
while (node.parent.color == RED) {
RBNode relativeNode = nil;
if (node.parent == node.parent.parent.left) {

relativeNode = node.parent.parent.right;
if (relativeNode != nil && relativeNode.color == RED) {
node.parent.color = BLACK;
relativeNode.color = BLACK;
node.parent.parent.color = RED;
node = node.parent.parent;
continue;
}
if (node == node.parent.right) {
//Double rotation needed
node = node.parent;
rotateLeft(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
//if the "else if" code hasn't executed, this
//is a case where we only need a single rotation
rotateRight(node.parent.parent);
} else {
relativeNode = node.parent.parent.left;
if (relativeNode != nil && relativeNode.color == RED) {
node.parent.color = BLACK;
relativeNode.color = BLACK;
node.parent.parent.color = RED;
node = node.parent.parent;
continue;

}
if (node == node.parent.left) {
//Double rotation needed
node = node.parent;
rotateRight(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
//if the "else if" code hasn't executed, this
//is a case where we only need a single rotation
rotateLeft(node.parent.parent);
}
}
root.color = BLACK;
}
/**
* The function Rotates the NODE
* to the left
* @param node
*/
void rotateLeft(RBNode node) {
if (node.parent != nil) {
if (node == node.parent.left) {
node.parent.left = node.right;
} else {
node.parent.right = node.right;

}
node.right.parent = node.parent;
node.parent = node.right;
if (node.right.left != nil) {
node.right.left.parent = node;
}
node.right = node.right.left;
node.parent.left = node;
} else {//Need to rotate root
RBNode right = root.right;
root.right = right.left;
right.left.parent = root;
root.parent = right;
right.left = root;
right.parent = nil;
root = right;
}
}
void rotateRight(RBNode node) {
if (node.parent != nil) {
if (node == node.parent.left) {
node.parent.left = node.left;
} else {
node.parent.right = node.left;
}

node.left.parent = node.parent;
node.parent = node.left;
if (node.left.right != nil) {
node.left.right.parent = node;
}
node.left = node.left.right;
node.parent.right = node;
} else {//Need to rotate root
RBNode left = root.left;
root.left = root.left.right;
left.right.parent = root;
root.parent = left;
left.right = root;
left.parent = nil;
root = left;
}
}
//Deletes whole tree
void deleteTree() {
root = nil;
}
/**
* Deletion
* @param target
* @param with

*/
void transplant(RBNode target, RBNode with) {
if (target.parent == nil) {
root = with;
} else if (target == target.parent.left) {
target.parent.left = with;
} else {
target.parent.right = with;
}
with.parent = target.parent;
}
/**
* Delete the
* @param z
* @return
*/
boolean delete(RBNode z) {
if ((z = searchNode(z, root)) == null) {
return false;
}
RBNode x;
RBNode y = z; // temporary reference y
int y_original_color = y.color;
if (z.left == nil) {
x = z.right;