Business Forecasting: Regression Analysis Case Study Report - BBA 315

This case study report analyzes visitor arrival data using regression analysis to forecast future trends. The report begins with a line chart of short-term visitor arrivals over four years, followed by the development of a multiple linear regression model incorporating a time variable and dummy variables for the month effect. The student explains the parameters, provides screenshots, and presents the overall regression equation. The report then interprets the intercept, time variable coefficient, and June dummy variable coefficient, and explains the meaning of the R-squared statistic. Regression equations for March, June, September, and December are derived, and a graph representing these equations is presented. The student conducts tests for the overall significance of the model and the individual significance of the time variable and December dummy variable coefficients. Finally, the report uses the regression equation to forecast tourist arrivals for months beyond the sample period and plots the original data against the forecasts, differentiating between the two.

Running head: REGRESSION ANALYSIS
REGRESSION ANALYSIS
Name of the Student
Name of the University
Author Note

1REGRESSION ANALYSIS
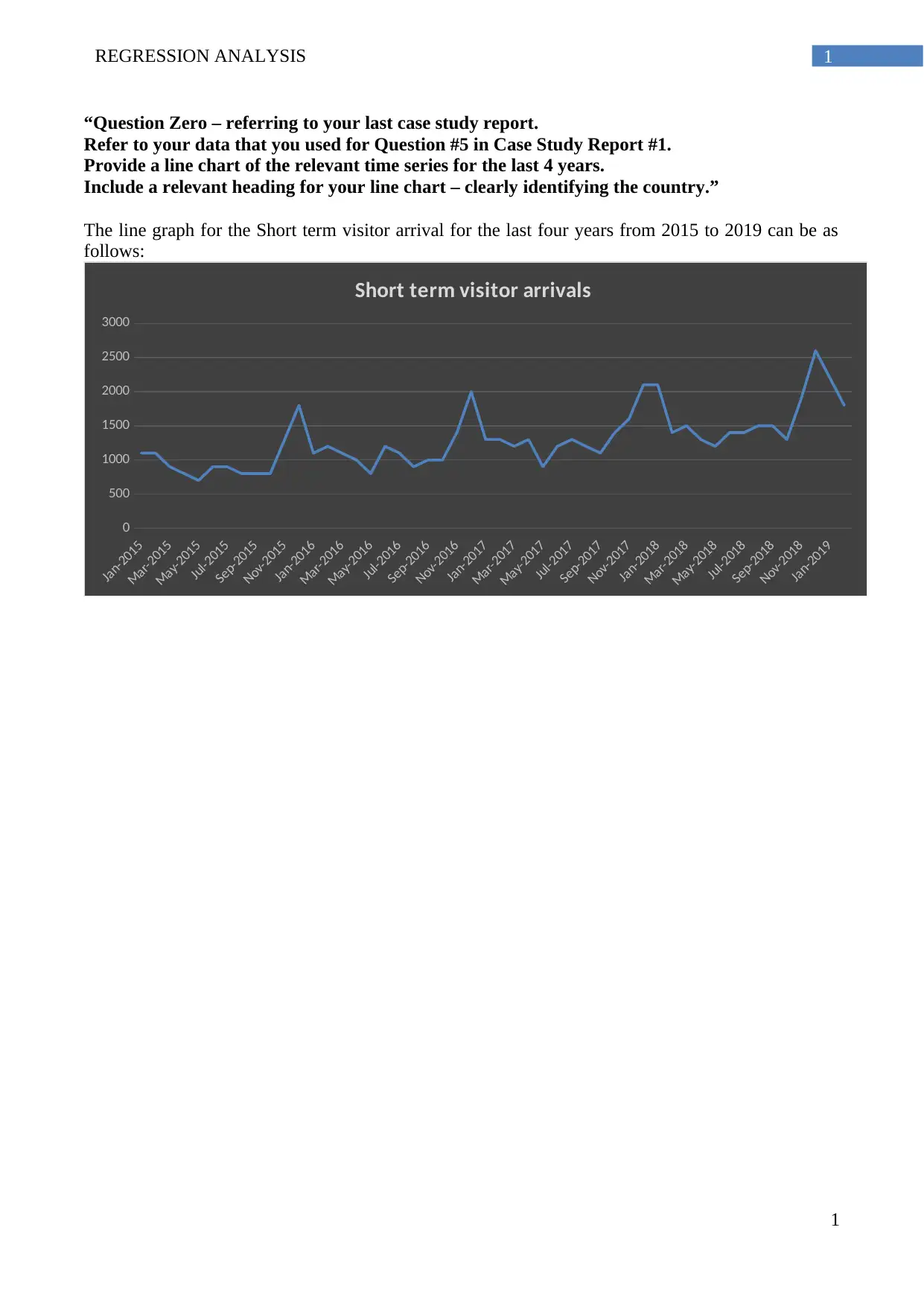
“Question Zero – referring to your last case study report.
Refer to your data that you used for Question #5 in Case Study Report #1.
Provide a line chart of the relevant time series for the last 4 years.
Include a relevant heading for your line chart – clearly identifying the country.”
The line graph for the Short term visitor arrival for the last four years from 2015 to 2019 can be as
follows:
Jan-2015
Mar-2015
May-2015
Jul-2015
Sep-2015
Nov-2015
Jan-2016
Mar-2016
May-2016
Jul-2016
Sep-2016
Nov-2016
Jan-2017
Mar-2017
May-2017
Jul-2017
Sep-2017
Nov-2017
Jan-2018
Mar-2018
May-2018
Jul-2018
Sep-2018
Nov-2018
Jan-2019
0
500
1000
1500
2000
2500
3000
Short term visitor arrivals
1

2REGRESSION ANALYSIS
Q1. “Estimate the parameters of a multiple linear regression model for visitor arrivals using an
intercept, a time variable and a suitable set of dummy variables for the month effect. Explain
what you have done, provide relevant screenshots, and write out the overall regression
equation.”
In order to find out the visitor arrival and find a multiple linear regression model for the
visitor arrival by making use of an intercept, the following parameters have to be determined:
Time variable
The time variable which has been chosen for the purpose of analysis can be understood t0 be
from the period March 2018 to 2019. This will help in ensuring that the latest trends are estimated
and that the visitors present in the country can be estimates successfully (Harrell Jr 2015).
Dummy variables
The dummy variables which have been chosen for the purpose of the years were made use of
is if analysis and they were written down in numbers (Carroll 2017).
dummy1 dumm2 y x x2 xy
Feb-2017 2 1 1300 0 0 0
Mar-2017 3 1 1200 1 1 3
Apr-2017 4 1 1300 2 4 16
May-2017 5 1 900 3 9 45
Jun-2017 6 1 1200 4 16 96
Jul-2017 7 1 1300 5 25 175
Aug-2017 8 1 1200 6 36 288
Sep-2017 9 1 1100 7 49 441
Oct-2017 10 1 1400 8 64 640
Nov-2017 11 1 1600 9 81 891
Dec-2017 12 1 2100 10 100 1200
Jan-2018 1 2 2100 -1 1 1
Feb-2018 2 2 1400 0 0 0
Mar-2018 3 2 1500 1 1 3
Apr-2018 4 2 1300 2 4 16
May-2018 5 2 1200 3 9 45
Jun-2018 6 2 1400 4 16 96
Jul-2018 7 2 1400 5 25 175
Aug-2018 8 2 1500 6 36 288
Sep-2018 9 2 1500 7 49 441
Oct-2018 10 2 1300 8 64 640
Nov-2018 11 2 1900 9 81 891
Dec-2018 12 2 2600 10 100 1200
Jan-2019 1 3 2200 -1 1 1
Feb-2019 2 3 1800 0 0 0
158 37700 108 772 7592
Intercept
2

3REGRESSION ANALYSIS
The value of the x be taken to be as 1 as it helps to understand the overall values of the
different years and the difference between the dummy variables chosen to replace the month and the
years
In order to ensure that two dummy variables were chosen for multiple linear regression model. A
total of 25 data sets were chosen which began from February 2017 to February 2019. Hence, in line
of this, the months were given a dummy variable of numbers 1 to 12 and the years were also labelled
accordingly from 1. These helped in figuring out the overall trend and the regression line as well.
Therefore, when the regression was carried out, the following data was received as a result:
Coefficie
nts
Standar
d Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Interce
pt 572.8261
296.07
9
1.9347
07
0.0666
11
-
42.903
9
1188.5
56
-
42.903
9
1188.5
56
2 43.47826
21.831
47
1.9915
4
0.0595
87
-
1.9227
7
88.879
29
-
1.9227
7
88.879
29
1 396.7391
120.85
03
3.2828
98
0.0035
49
145.41
72
648.06
1
145.41
72
648.06
1
This means that the regression line is
Y=572.82+43.47(YEAR) +396.7(Month)
Hence, the intercept is 572.82 approximately
Q2. “Explain the meaning of the intercept, the coefficient of the time variable, as well as the
coefficient for the June dummy variable. (If June is your baseline, then change June to
September).”
 Intercept: In such a scenario, the intercept can be understood to be relatively stable in nature
and hence, it reflects that the intercept can be stated to have a major influence on the Y
variable. The intercept can be understood to be the expected mean value of Y in case X is
considered to be 0 (Darlington and Hayes 2016). Very often when X=0 then the intercept is
the expected mean of the Y value.
 Coefficient of time variable: The coefficient of the time variable in such a scenario tends to
take into consideration the time gap which exists between the given time range. In such a
case the time variable has been taken to be a gap of one month which predicts the customer in
take every period (Fox 2015).
 Coefficient for the June dummy variable: The coefficient of June variable can be understood
to be moderate in nature which reflects that the customer intake is maximum in this given
period of time (Chatterjee and Hadi 2015).

3

4REGRESSION ANALYSIS
Q3. “What is the R-squared for your regression? Explain what this represents, and comment
on the importance (or not) of this statistic.”
As seen from the given graph the value of the R squared for the regression which was carried
out can be understood to be 0.951367786. The R squared can be rightfully understood to be the
goodness of the fit measure for the linear equation models. The statistic tends to represent the
percentage of variance which tends to exist in the dependent variable in relation to the independent
variable explained collectively (Cohen, West and Aiken 2014). The R-Squared measures the overall
strength of the relationship between the model chosen for the purpose of the analysis and the
dependent variable which has been chosen and the dependent variable which is here the case of the
incoming variables (Hayes 2017). The R squared measures this relationship on a convenient scale of
0 to 100%. This tends to reflect that since the value of the R squared in the particular problem seems
to be 95% which can be taken to be a good figure of the measure and hence, it represents that the
regression model chosen for the prediction of the problem is a good model and that it has the
capability to explain the values of the dependent variable which is the number of members visiting
Columbia.
Regression Statistics
Multiple R
0.97538084
1
R Square
0.95136778
6
Adjusted R
Square
0.90370268
5
Standard Error
361.018467
2
Observations 24
Q5. “Write out the regression equation for each of the following months: March, June,
September, and December. Draw a graph that represents the four different regression lines for
each of the following months: March, June, September, and December.”
From the analysis as done in the first question, the regression equations for the month, March,
June, September and December can be stated to be as follows:
March- Y=572.82+43.47(3) +396.7(3)
June-Y=572.82+43.47(6) +396.7(3)
September- Y=572.82+43.47(9) +396.7(3)
December- Y=572.82+43.47(12) +396.7(3)
Hence, the following data can be present:
4

5REGRESSION ANALYSIS
Feb-19 Mar-19 May-19 Jul-19 Aug-19 Oct-19 Dec-19 Jan-20
0
1000
2000
3000
4000
5000
6000
f(x) = 0.0843260822653297 x
R² = 0.885794265305255
Regression Chart
5

6REGRESSION ANALYSIS
Q5. “Conduct a test for the overall significance of the model. Explain and analyses your
results.”
df SS MS F
Significan
ce F
Regressi
on 2
13197
46
659873
.2
5.6942
03 0.010573
Residual 21
24335
87
115885
.1
Total 23
37533
33
The F test in a regression can be understood as the overall test which is conducted in
regression and tends to compare the overall fir of the different linear models. Unlike the different t
tests which re conducted by the different users, the t tests can access only a single coefficient at a
time whereas the multiple coefficient`s test can be conducted through an F test. The F test is a
significant model which tends to compare the model with no predictors with the one which is
specified. When the model contains no predictors it is known as an intercept only model (Breiman
2017).
The P value for the F test is calculated which helps in understanding the overall significance.
In order to understand whether the regression model as chosen by the user is a better fit to the
scenario than a one with no independent variables, the F test is conducted which helps in and fits
with the regression statistics such as the R squared. The F test significant test can be stated to be very
flexible and can be used in a variety of settings. They have the capability to evaluate the multiple
model terms simultaneously which helps in comparing with other models. The F test undertakes the
null and the alternate hypothesis (Hoffmann and Shafer 2015). The former states that the model
without a variables is better suited whereas the latter states that model with the variables is better.
The test is considered to be crucial because, it helps in ensuring that the independent
variables in the model improve the overall fit whereas, with just the intercept the model would not be
sufficient.
Q6. “Conduct a test for the individual significance of the coefficient for the time variable.
Explain and analyze your results.”
“Conduct a test for the individual significance of the coefficient for the December dummy
variable. (If December is your baseline, then change December to March). Explain and analyze
your results.”
Coefficien
ts
Standar
d Error t Stat P-value
Interce
pt 572.8261 296.079
1.93470
7
0.06661
1
2 43.47826
21.8314
7 1.99154
0.05958
7
1 396.7391
120.850
3
3.28289
8
0.00354
9
The t tests can be understood to be used to conduct the hypothesis tests on the regression
coefficients which have been obtained in the simple linear regression. The test goes a long way in
estimating whether the presence of the individual coefficient is adding any weightage to the model or
6

7REGRESSION ANALYSIS
not (Hox, Moerbeek and Van de Schoot 2017). The hypothesis is generally used to test the
coefficient for any month Dummy as possible. The t test is generally based on the t equation and also
is supported by the standard error. In this case, for the Dummy of the month table, as the
Significance is 3.28 which is clearly more than the P value of 0.035, the coefficient can be taken to
be significant in nature.
Q7. ``Use your regression equation to forecast tourist arrivals for each month beyond your
sample period. Show your working for only the December forecast as an example. Plot your
original data against time and include your forecasts. Clearly differentiate between the original
data and the forecasts.”
As understood from the previous analysis, the overall regression equation which was arrived
at can be stated to be as follows:
Y=572.82+43.47(YEAR) +396.7(Month)
Hence, in any case if the overall prediction of the tourist has to be calculated for the month of
December, then in such a case, it becomes considerably crucial for the user to ensure that the values
are fitted in for the given year as present. This means that if the incoming for the month December
has to be taken out then for the year -2019 the vale dummy 3 has been taken and for the month
December the dummy 12 has been taken and in such a case, it is important to ensure that, the value
of the tourists are accurate in nature and hence, when in the given equation, year is replaced with the
dummies then the following can be understood to be the overall result.
Y=572.82+43.47(12) +396.7(3)
=5464 customers
Hence, in a similar manner predictions for any month can be done accordingly.
The predictions done for March, June, September and December as done previously can be used in
this case as a representation of the future incoming tourists.
Feb-2017
Apr-2017
Jun-2017
Aug-2017
Oct-2017
Dec-2017
Feb-2018
Apr-2018
Jun-2018
Aug-2018
Oct-2018
Dec-2018
Feb-2019
Apr-2019
Jun-2019
Aug-2019
Oct-2019
Dec-2019
0
1000
2000
3000
4000
5000
6000
130012001300
900
1200130012001100
1400
1600
21002100
14001500
13001200
1400140015001500
1300
1900
2600
2200
18001893
3084
4274
5464
Incoming customers
The given image provides the plotted graph of the same. It assists in ensuring that the overall
analysis as received is capable of forecasting in the long run.
Q.8 “Based on your analyses above, are there any modifications that you would suggest to
arrive at an improved regression model?
7

8REGRESSION ANALYSIS
Compare and contrast the performance of your model from Case Study Report #1 and your
regression model above. Based on your analysis, which model would you utilize for your
specific business case?”
In order to make the overall regression analysis as carried out better, it is crucial for the user
of the model to conduct an overall exploratory analysis which looks at the plots of the different
explanatory variables as well as the responsive variables in order to determine whether the right fit is
being used or not (Sperandei 2014). This helps to signify the relationship between the x and the y
and cannot be deemed to be necessarily linear.
Moreover, another way to improve the overall model, can be understood to be the face that
the user must not just concentrate on the r squared, the adjusted r square or the other such variables
but it is more important to know that the use of a model should be made which tends to fit the data
well as is simple in nature (Schroeder, Sjoquist and Stephan 2016). The predictors needs to be
relevant to the response. Removal of the data solely because of the reason that it is difficult to judge
the unusual value is incorrect and hence, unless dome error is determined this step should not be
undertaken.
In addition to this, if one is considered worried about the outliers then the robust regression
can be understood to be the key to success and the R has to be the tool of choice for the MASS
package which provides easy to use methods for the fitting nodes based on the M estimates. In
addition to this, various packages can also be found to perform the regression on the basis of the rank
based estimation as well.
Hence, using a robust model for the calculation is important as it influences the fit and the accuracy
of the same.
As compared to the previous study done on Case 1 it can be stated that, the linear regression
model would have been appropriate for the given case as it helps in the analysis of the customer’s
incoming simply based on the years. In the linear regression model, it would have been simpler to
predict the data and hence, it would have been proved as a better fit for the model (Sagoe et al.
2014).
8

9REGRESSION ANALYSIS
References
Breiman, L., 2017. Classification and regression trees. Routledge.
Carroll, R.J., 2017. Transformation and weighting in regression. Routledg
Chatterjee, S. and Hadi, A.S., 2015. Regression analysis by example. John Wiley & Sons.
Cohen, P., West, S.G. and Aiken, L.S., 2014. Applied multiple regression/correlation analysis for the
behavioral sciences. Psychology Press.
Darlington, R.B. and Hayes, A.F., 2016. Regression analysis and linear models: Concepts,
applications, and implementation. Guilford Publications.
Fox, J., 2015. Applied regression analysis and generalized linear models. Sage Publications.
Harrell Jr, F.E., 2015. Regression modeling strategies: with applications to linear models, logistic
and ordinal regression, and survival analysis. Springer.
Hayes, A.F., 2017. Introduction to mediation, moderation, and conditional process analysis: A
regression-based approach. Guilford Publications.
Hoffmann, J.P. and Shafer, K., 2015. Linear regression analysis. Washington, DC: NASW Press.
Hox, J.J., Moerbeek, M. and Van de Schoot, R., 2017. Multilevel analysis: Techniques and
applications. Routledge.
Sagoe, D., Molde, H., Andreassen, C.S., Torsheim, T. and Pallesen, S., 2014. The global
epidemiology of anabolic-androgenic steroid use: a meta-analysis and meta-regression
analysis. Annals of epidemiology, 24(5), pp.383-398.
Schroeder, L.D., Sjoquist, D.L. and Stephan, P.E., 2016. Understanding regression analysis: An
introductory guide (Vol. 57). Sage Publications.
Sperandei, S., 2014. Understanding logistic regression analysis. Biochemia medica: Biochemia
medica, 24(1), pp.12-18.
9

10REGRESSION ANALYSIS
Appendices
The Analysis
SUMMARY OUTPUT
Regression Statistics
Multiple R
0.59297
5
R Square 0.35162
Adjusted R
Square
0.28986
9
Standard
Error 340.419
Observations 24
ANOVA
df SS MS F
Significan
ce F
Regression 2 1319746
65987
3.2
5.6942
03 0.010573
Residual 21 2433587
11588
5.1
Total 23 3753333
Coeffici
ents
Standard
Error t Stat
P-
value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept
572.826
1 296.079
1.9347
07
0.0666
11 -42.9039
1188.55
6 -42.9039 1188.556
2
43.4782
6 21.83147
1.9915
4
0.0595
87 -1.92277
88.8792
9 -1.92277 88.87929
1
396.739
1 120.8503
3.2828
98
0.0035
49 145.4172 648.061 145.4172 648.061
10