Statistical Regression Analysis and Diagnostics Report 2020

This assignment solution provides a comprehensive analysis of regression models and residual diagnostics. It begins with descriptive statistics for ten variables, including mean, median, quartiles, and skewness. The solution then assesses five regression models (fit1 to fit5), checking for outliers, normality, homoscedasticity, multicollinearity, and linearity. Diagnostic tests such as outlierTest, ncvTest, and vif are used to validate model assumptions. Additionally, the assignment includes an analysis of the 'prestige' dataset, creating scatter plot matrices and descriptive statistics. Finally, distinct simple regression models are built to predict prestige based on education, income and gender, evaluating their significance and R-squared values. The analysis uses statistical tools and tests to ensure the robustness and validity of the regression models.

UNIVARIATE ANALYSIS II: REGRESSION
Student Name:
Instructor Name:
Course Number:
20th February 2020

Q1: Descriptive statistics
The table below presents the descriptive (summary) statistics for the 10 variables under study.
The statistics presented include the mean, median, quartiles (1st and 3rd quartiles), minimum,
maximum, range, skewness, kurtosis and standard error.
> describe(Assignment2)
vars n mean sd median 1st Qu. 3rd Qu. min max range skew kurtosis se
X 1 250 125.50 72.31 125.50 63.25 187.75 1.00 250.00 249.00 0.00 -1.21 4.57
y1 2 250 612.57 277.57 589.00 374.5 818.2 118.00 1254.00 1136.00 0.15 -0.97 17.56
y2 3 250 10.00 2.25 9.41 8.389 11.12 6.00 16.14 10.13 0.84 -0.04 0.14
y3 4 250 57.97 28.63 59.00 35.00 79.00 1.00 116.00 115.00 -0.01 -1.02 1.81
y4 5 250 519.37 106.69 515.64 422.80 614.8 317.77 701.12 383.35 -0.04 -1.50 6.75
y5 6 250 809.56 146.92 802.00 683.80 932.8 552.00 1097.00 545.00 0.08 -1.13 9.29
x1 7 250 51.49 26.93 50.00 29.00 73.75 2.00 100.00 98.00 0.04 -1.12 1.70
x2 8 250 4.78 3.27 5.00 2.00 8.00 0.00 10.00 10.00 0.17 -1.23 0.21
x3 9 250 52.38 27.88 54.00 32.25 76.00 1.00 100.00 99.00 -0.13 -1.09 1.76
x4 10 250 99.92 21.35 102.99 79.81 119.05 58.94 138.73 79.79 -0.04 -1.57 1.35
x5 11 250 73.25 14.69 73.00 59.25 85.00 50.00 100.00 50.00 0.11 -1.16 0.93
The following figures are the histograms with the normal curves for the variables y1, y2, y3, y4 and y5.

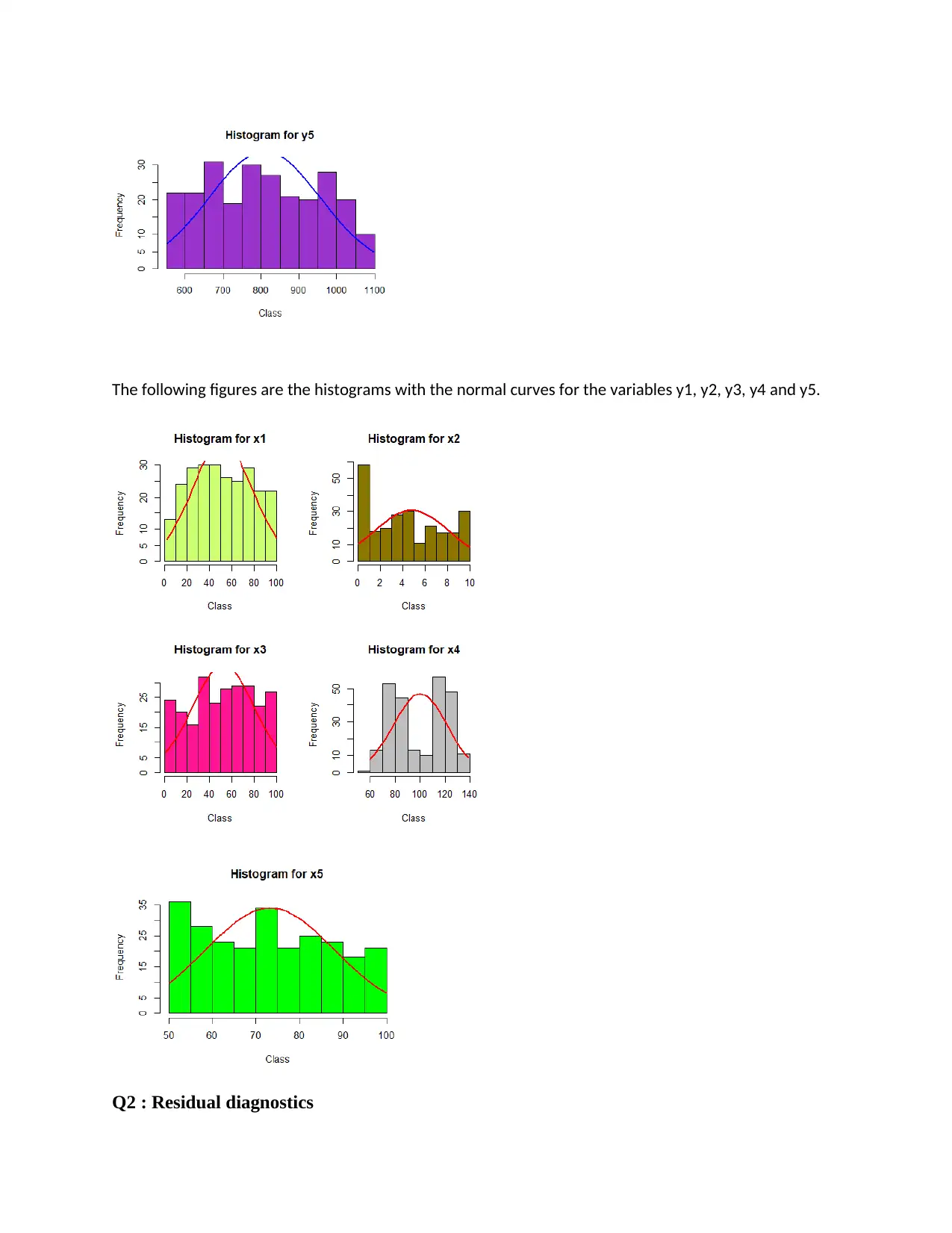
The following figures are the histograms with the normal curves for the variables y1, y2, y3, y4 and y5.
Q2 : Residual diagnostics

Model 1 :
y1=β0 + β1 x1 + β2 x2+ β3 x3+ e
> fit1 <- lm(y1 ~ x1 + x2 + x3, data=Assignment2)
> summary(fit1)
Call:
lm(formula = y1 ~ x1 + x2 + x3, data = Assignment2)
Residuals:
Min 1Q Median 3Q Max
-215.848 -32.376 -1.139 33.613 259.824
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 108.3579 13.4049 8.083 2.85e-14 ***
x1 10.0116 0.1519 65.893 < 2e-16 ***
x2 -0.1013 1.2483 -0.081 0.935
x3 -0.2058 0.1466 -1.404 0.162
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 64.25 on 246 degrees of freedom
Multiple R-squared: 0.9471, Adjusted R-squared: 0.9464
F-statistic: 1467 on 3 and 246 DF, p-value: < 2.2e-16
Diagnostic tests
Checking for outliers
> outlierTest(fit1)
rstudent unadjusted p-value Bonferroni p
110 4.231183 3.2873e-05 0.0082184

The above plots and tests shows that there is
evidence of outliers in the residuals for the model 1.
Checking for normality
The histogram above shows that the residuals follow a normal distribution.
Checking for equal variances/homoscedasticity
> ncvTest(fit1)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 82.12735, Df = 1, p = < 2.22e-16

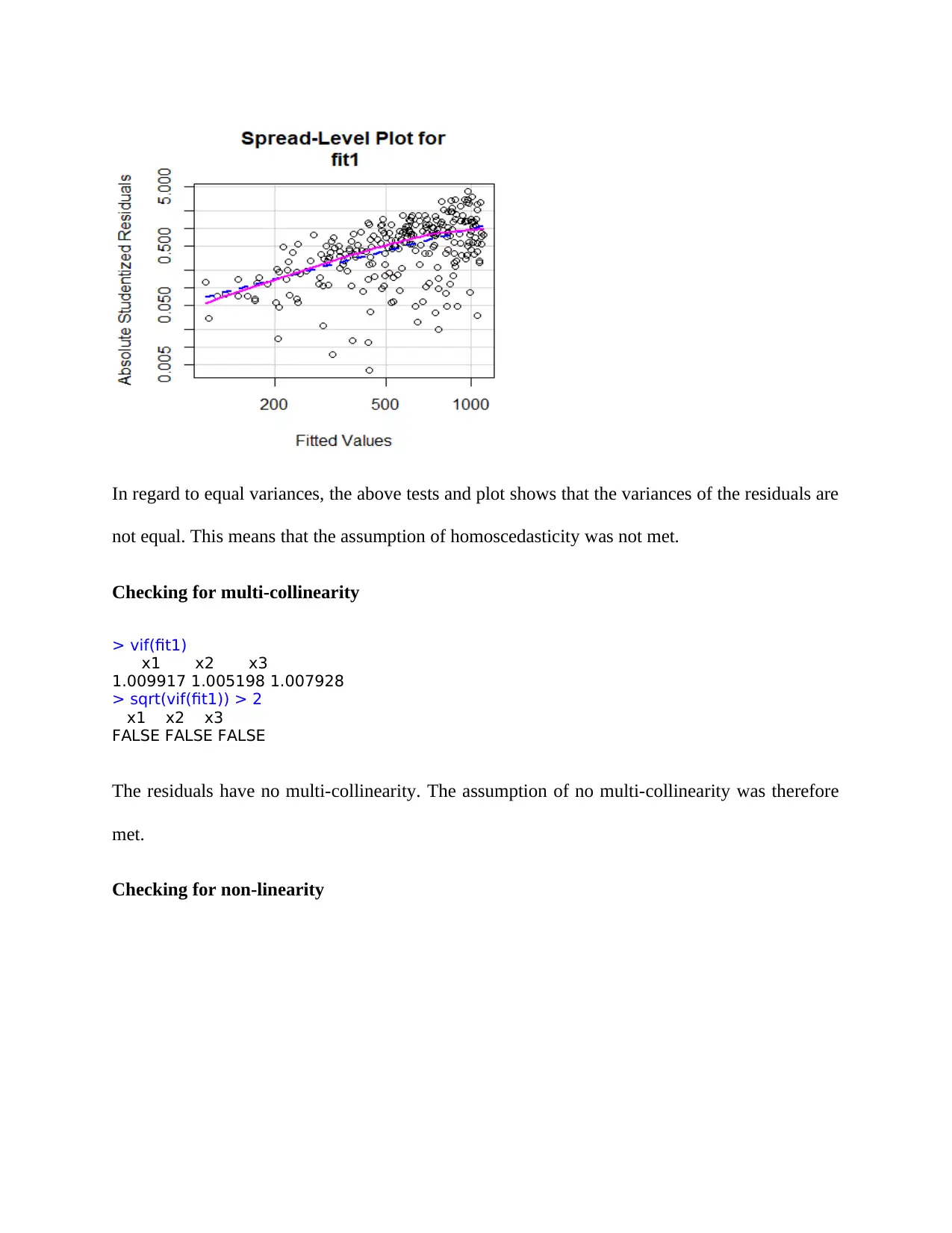
In regard to equal variances, the above tests and plot shows that the variances of the residuals are
not equal. This means that the assumption of homoscedasticity was not met.
Checking for multi-collinearity
> vif(fit1)
x1 x2 x3
1.009917 1.005198 1.007928
> sqrt(vif(fit1)) > 2
x1 x2 x3
FALSE FALSE FALSE
The residuals have no multi-collinearity. The assumption of no multi-collinearity was therefore
met.
Checking for non-linearity

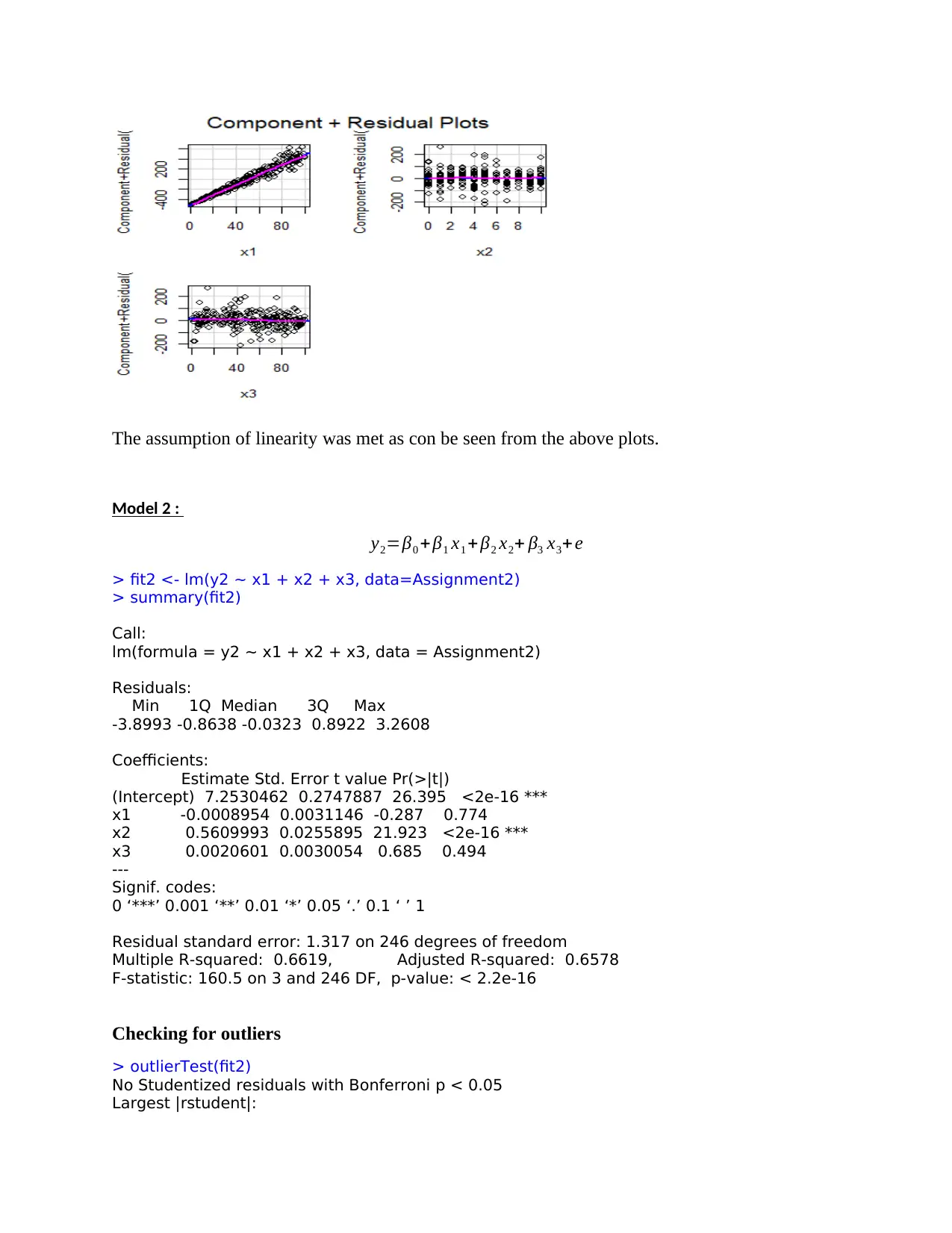
The assumption of linearity was met as con be seen from the above plots.
Model 2 :
y2=β0 + β1 x1 + β2 x2+ β3 x3+ e
> fit2 <- lm(y2 ~ x1 + x2 + x3, data=Assignment2)
> summary(fit2)
Call:
lm(formula = y2 ~ x1 + x2 + x3, data = Assignment2)
Residuals:
Min 1Q Median 3Q Max
-3.8993 -0.8638 -0.0323 0.8922 3.2608
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.2530462 0.2747887 26.395 <2e-16 ***
x1 -0.0008954 0.0031146 -0.287 0.774
x2 0.5609993 0.0255895 21.923 <2e-16 ***
x3 0.0020601 0.0030054 0.685 0.494
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.317 on 246 degrees of freedom
Multiple R-squared: 0.6619, Adjusted R-squared: 0.6578
F-statistic: 160.5 on 3 and 246 DF, p-value: < 2.2e-16
Checking for outliers
> outlierTest(fit2)
No Studentized residuals with Bonferroni p < 0.05
Largest |rstudent|:

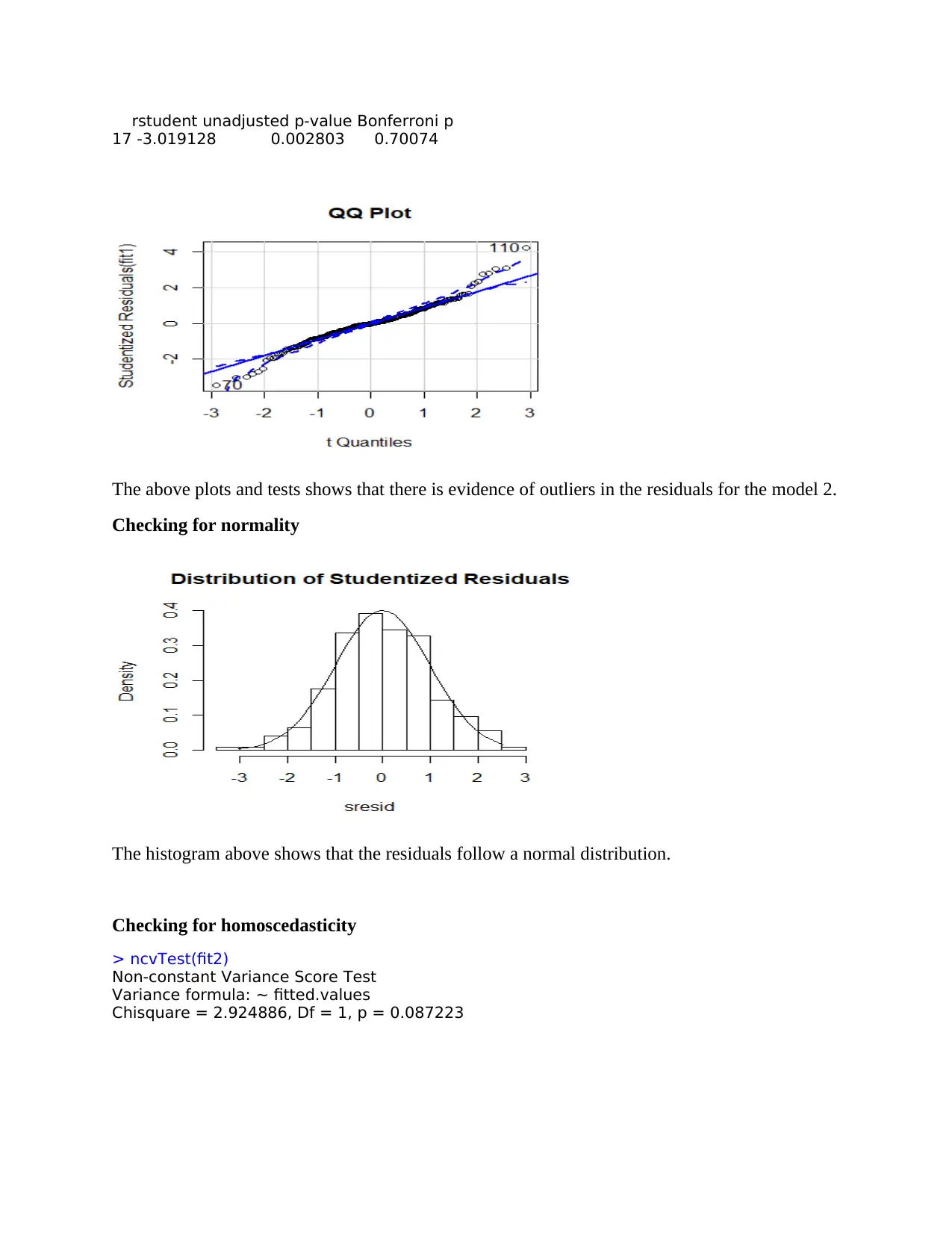
rstudent unadjusted p-value Bonferroni p
17 -3.019128 0.002803 0.70074
The above plots and tests shows that there is evidence of outliers in the residuals for the model 2.
Checking for normality
The histogram above shows that the residuals follow a normal distribution.
Checking for homoscedasticity
> ncvTest(fit2)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 2.924886, Df = 1, p = 0.087223

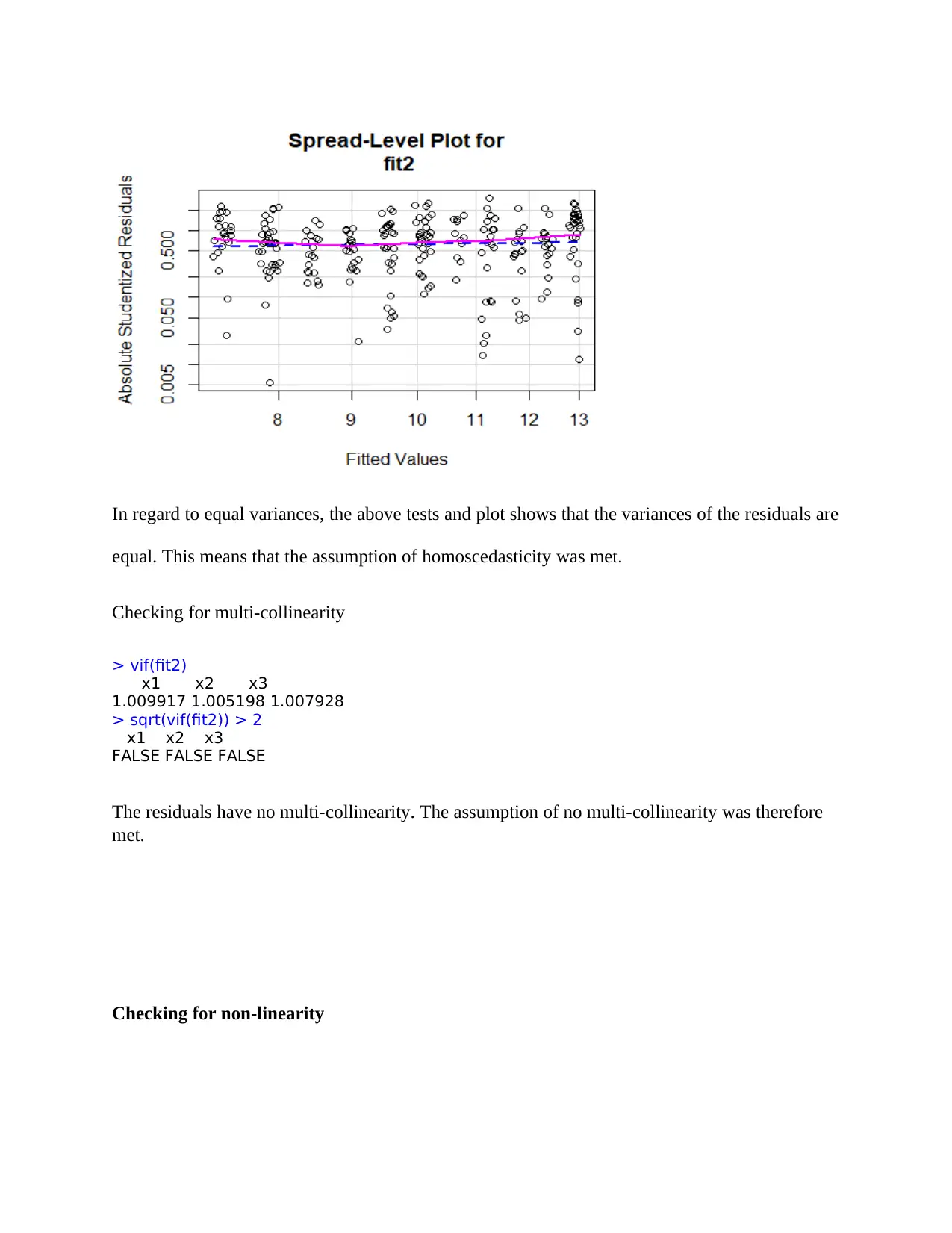
In regard to equal variances, the above tests and plot shows that the variances of the residuals are
equal. This means that the assumption of homoscedasticity was met.
Checking for multi-collinearity
> vif(fit2)
x1 x2 x3
1.009917 1.005198 1.007928
> sqrt(vif(fit2)) > 2
x1 x2 x3
FALSE FALSE FALSE
The residuals have no multi-collinearity. The assumption of no multi-collinearity was therefore
met.
Checking for non-linearity

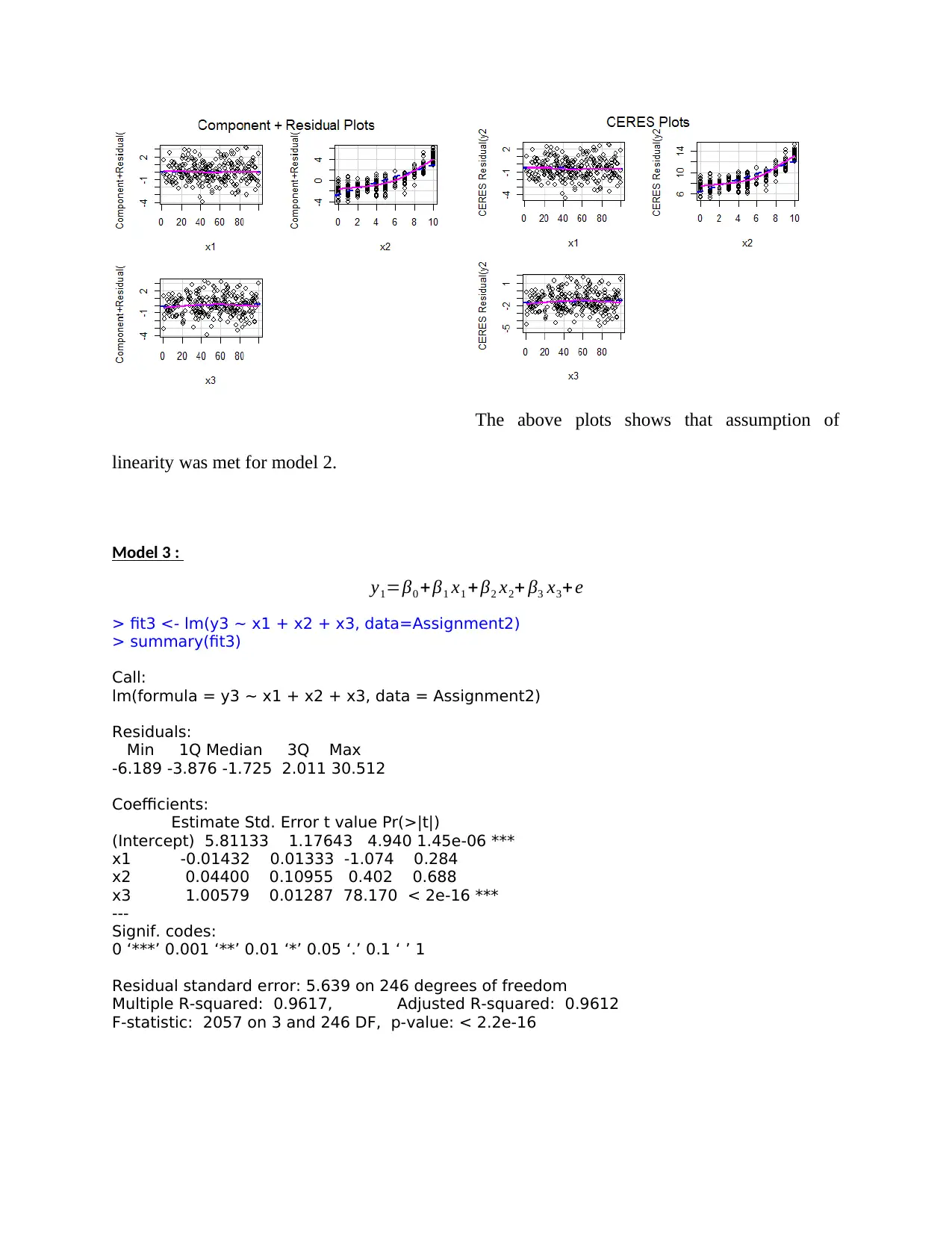
The above plots shows that assumption of
linearity was met for model 2.
Model 3 :
y1=β0 + β1 x1 + β2 x2+ β3 x3+ e
> fit3 <- lm(y3 ~ x1 + x2 + x3, data=Assignment2)
> summary(fit3)
Call:
lm(formula = y3 ~ x1 + x2 + x3, data = Assignment2)
Residuals:
Min 1Q Median 3Q Max
-6.189 -3.876 -1.725 2.011 30.512
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.81133 1.17643 4.940 1.45e-06 ***
x1 -0.01432 0.01333 -1.074 0.284
x2 0.04400 0.10955 0.402 0.688
x3 1.00579 0.01287 78.170 < 2e-16 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.639 on 246 degrees of freedom
Multiple R-squared: 0.9617, Adjusted R-squared: 0.9612
F-statistic: 2057 on 3 and 246 DF, p-value: < 2.2e-16

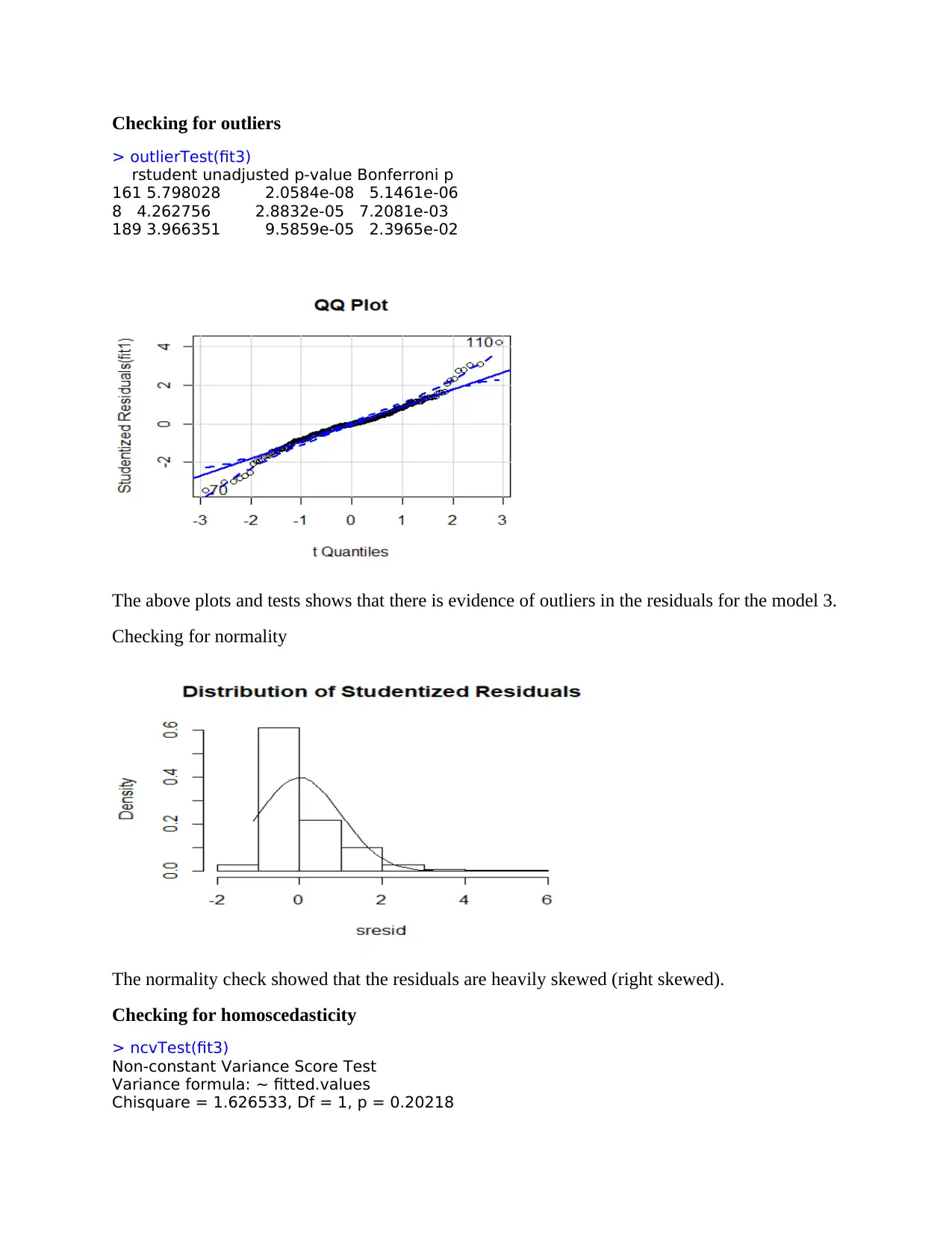
Checking for outliers
> outlierTest(fit3)
rstudent unadjusted p-value Bonferroni p
161 5.798028 2.0584e-08 5.1461e-06
8 4.262756 2.8832e-05 7.2081e-03
189 3.966351 9.5859e-05 2.3965e-02
The above plots and tests shows that there is evidence of outliers in the residuals for the model 3.
Checking for normality
The normality check showed that the residuals are heavily skewed (right skewed).
Checking for homoscedasticity
> ncvTest(fit3)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 1.626533, Df = 1, p = 0.20218

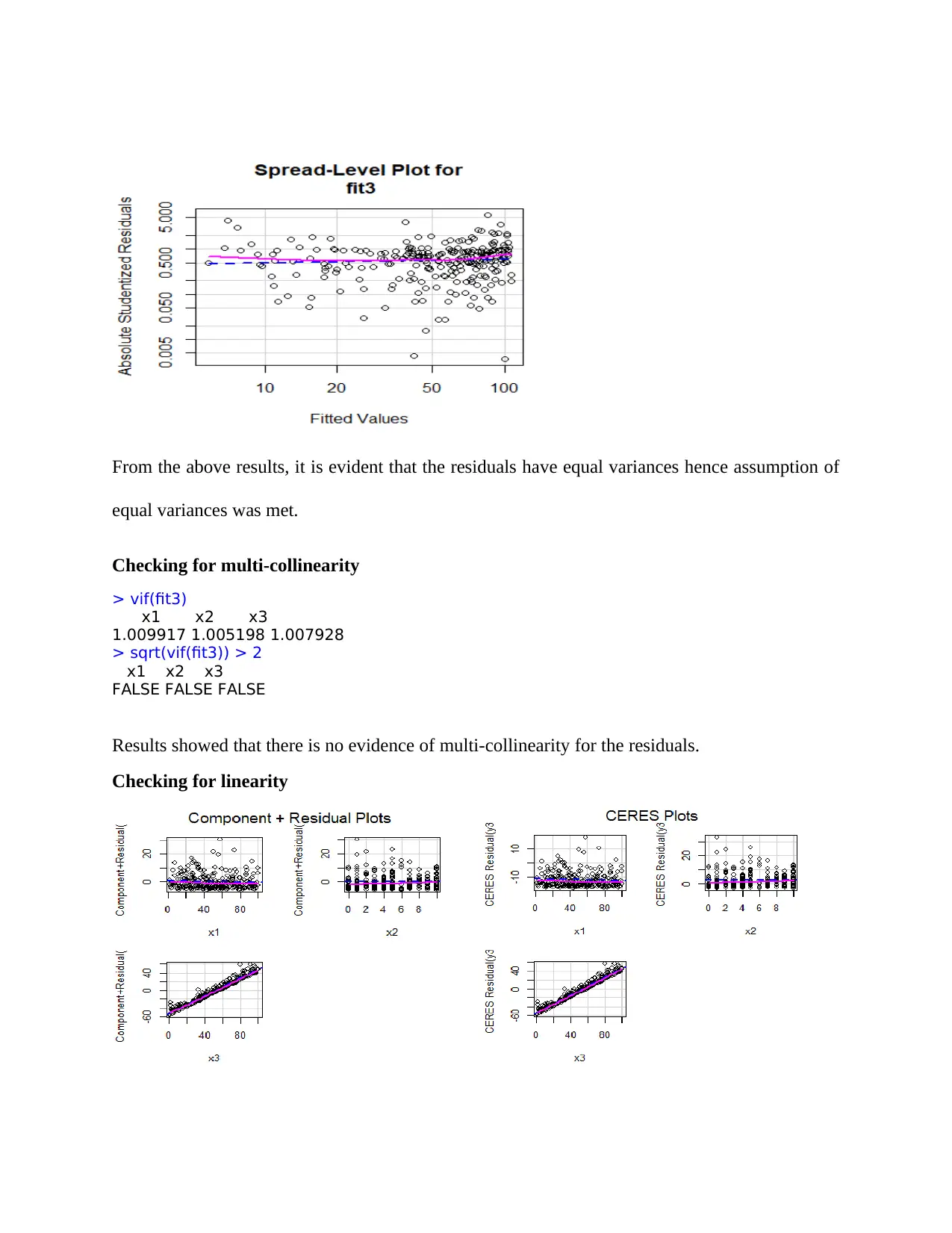
From the above results, it is evident that the residuals have equal variances hence assumption of
equal variances was met.
Checking for multi-collinearity
> vif(fit3)
x1 x2 x3
1.009917 1.005198 1.007928
> sqrt(vif(fit3)) > 2
x1 x2 x3
FALSE FALSE FALSE
Results showed that there is no evidence of multi-collinearity for the residuals.
Checking for linearity

The above plots shows that the residuals are linear hence; the assumption of linearity was met for
model 3.
Model 4 :
y4 =β0+ β1 x4 + β2 x5 +e
> fit4 <- lm(y4 ~ x4 + x5, data=Assignment2)
> summary(fit4)
Call:
lm(formula = y4 ~ x4 + x5, data = Assignment2)
Residuals:
Min 1Q Median 3Q Max
-49.415 -10.793 0.632 11.261 33.834
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.06037 6.58169 2.136 0.0336 *
x4 4.95100 0.04406 112.372 <2e-16 ***
x5 0.14490 0.06403 2.263 0.0245 *
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 14.84 on 247 degrees of freedom
Multiple R-squared: 0.9808, Adjusted R-squared: 0.9807
F-statistic: 6314 on 2 and 247 DF, p-value: < 2.2e-16
Checking for outliers
> outlierTest(fit4)
No Studentized residuals with Bonferroni p < 0.05
Largest |rstudent|:
rstudent unadjusted p-value Bonferroni p
161 -3.42722 0.00071462 0.17865

From the above results, it is clear that there are few outliers in the dataset.
Checking for normality
The above histogram shows that there is a slight skewness in the residuals. This shows that the
normality assumption is not met.
Checking for homoscedasticity
> ncvTest(fit4)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 0.1690118, Df = 1, p = 0.68099

The above results shows that the homoscedasticity assumption of the residuals is met (p > 0.05).
Checking for multi-collinearity
> vif(fit4)
x4 x5
1.000665 1.000665
> sqrt(vif(fit4)) > 2
x4 x5
FALSE FALSE
The above results shows that there is no multi-collinearity in the dataset hence the assumption of
no multi-collinearity was met.
Checking for linearity
From the above plots, it is evident that the assumption of linearity was met.
Model 5 :
y5=β0 + β2 x5 +e

> fit5 <- lm(y5 ~ x5, data=Assignment2)
> summary(fit5)
Call:
lm(formula = y5 ~ x5, data = Assignment2)
Residuals:
Min 1Q Median 3Q Max
-29.578 -13.637 -0.293 12.049 200.422
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 85.68308 7.26573 11.79 <2e-16 ***
x5 9.88260 0.09726 101.61 <2e-16 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 22.55 on 248 degrees of freedom
Multiple R-squared: 0.9765, Adjusted R-squared: 0.9764
F-statistic: 1.032e+04 on 1 and 248 DF, p-value: < 2.2e-16
Checking for outliers
> outlierTest(fit5)
rstudent unadjusted p-value Bonferroni p
75 10.845123 1.1442e-22 2.8605e-20
50 8.799492 2.4284e-16 6.0709e-14
From the above results, it is evident that there are few outliers in the residuals.
Checking for normality

The above histogram shows that the normality assumption was violated. The residuals are
heavily skewed to the right.
Checking for homoscedasticity
> ncvTest(fit5)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 25.98431, Df = 1, p = 3.442e-07
The above results shows that the residuals did not meet the assumption of equal variances.
Checking linearity

The above figure shows that assumption on linearity was met.
Q3: using dataset #2 (prestige dataset)
Scatter plot matrix
Descriptive statistics
> describe(Prestige_new)
vars n mean sd median trimmed mad min max range
education 1 102 10.74 2.73 10.54 10.63 3.15 6.38 15.97 9.59
income 2 102 6797.90 4245.92 5930.50 6161.49 3060.83 611.00 25879.00 25268.00
women 3 102 28.98 31.72 13.60 24.74 18.73 0.00 97.51 97.51
prestige 4 102 46.83 17.20 43.60 46.20 19.20 14.80 87.20 72.40
Q4: Distinct Simple Regression models
Model 1:
prestige=β0 +β1 ( education ) +e
> model1 <- lm(prestige ~ education, data=Prestige_new)
> summary(model1)
Call:

lm(formula = prestige ~ education, data = Prestige_new)
Residuals:
Min 1Q Median 3Q Max
-26.0397 -6.5228 0.6611 6.7430 18.1636
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -10.732 3.677 -2.919 0.00434 **
education 5.361 0.332 16.148 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.103 on 100 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.7228, Adjusted R-squared: 0.72
F-statistic: 260.8 on 1 and 100 DF, p-value: < 2.2e-16
A simple linear regression was performed to predict prestige based on the participant's education.
A significant regression equation was found (F(1, 100) = 260.8, p = .000), with an R2 of 0.7228.
The value of R2 shows that 72.28% of the variation in the participant’s prestige is explained by
education. Participants’ predicted prestige is given as follows;
−10.732+5.361(education)
Model 2:
prestige=β0 + β1 ( income ) +e
> model2 <- lm(prestige ~ income, data=Prestige_new)
> summary(model2)
Call:
lm(formula = prestige ~ income, data = Prestige_new)
Residuals:
Min 1Q Median 3Q Max
-33.007 -8.378 -2.378 8.432 32.084
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.714e+01 2.268e+00 11.97 <2e-16 ***
income 2.897e-03 2.833e-04 10.22 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.09 on 100 degrees of freedom
(1 observation deleted due to missingness)

Multiple R-squared: 0.5111, Adjusted R-squared: 0.5062
F-statistic: 104.5 on 1 and 100 DF, p-value: < 2.2e-16
A simple linear regression was performed to predict prestige based on the participant's income. A
significant regression equation was found (F(1, 100) = 104.5, p = .000), with an R2 of 0.5111.
The value of R2 shows that 51.11% of the variation in the participant’s prestige is explained by
income. Participants’ predicted prestige is given as follows;
0.2714+ 0.002897(income)
Model 3:
prestige=β0 +β1 ( women ) +e
> model3 <- lm(prestige ~ women, data=Prestige_new)
> summary(model3)
Call:
lm(formula = prestige ~ women, data = Prestige_new)
Residuals:
Min 1Q Median 3Q Max
-33.444 -12.391 -4.126 13.034 39.185
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 48.69300 2.30760 21.101 <2e-16 ***
women -0.06417 0.05385 -1.192 0.236
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 17.17 on 100 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.014, Adjusted R-squared: 0.004143
F-statistic: 1.42 on 1 and 100 DF, p-value: 0.2362
A simple linear regression was performed to predict prestige based on participant’s gender. A
non-significant regression equation was found (F(1, 100) = 1.42, p = .236), with an R2 of 0.014.
The value of R2 shows that women explain only 1.4% of the variation in the participant’s
prestige. Participants’ predicted prestige is given as follows;
49.693−0.0642( women)

Q5: Multiple Regression analysis
Model 4:
prestige=β0 + β1 ( education ) +β2 ( income )+ β3 ( women )+ e
> model4 <- lm(prestige ~ education + income + women, data=Prestige_new)
> summary(model4)
Call:
lm(formula = prestige ~ education + income + women, data = Prestige_new)
Residuals:
Min 1Q Median 3Q Max
-19.8246 -5.3332 -0.1364 5.1587 17.5045
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.7943342 3.2390886 -2.098 0.0385 *
education 4.1866373 0.3887013 10.771 < 2e-16 ***
income 0.0013136 0.0002778 4.729 7.58e-06 ***
women -0.0089052 0.0304071 -0.293 0.7702
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.846 on 98 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.7982, Adjusted R-squared: 0.792
F-statistic: 129.2 on 3 and 98 DF, p-value: < 2.2e-16
Brief comment on the MLR compared to the simple regression
Compared to the three previous models, it can be seen there is an increase in the values of the R-
squared for model 4 (multiple linear regression that has three independent variables). This shows
that a MLR performs much better as it includes all the necessary factors that are ideal for
predicting the dependent variable.
Short paragraph on the MLR
A multiple linear regression was performed to predict prestige based on the participant's
education, income and women. A significant regression equation was found (F(3, 98) = 129.2, p

= .000), with an R2 of 0.7982. The value of R2 shows that the three independent variables
education, income and women) explain only 79.82% of the variation in the participant’s prestige.
Participants’ predicted prestige is given as follows;
−6.794+ 4.187 ( education ) +0.001( income)−0.0089(women)
Women was found to be insignificant in predicting prestige while both education and income
were found to be significant in predicting the prestige.
The coefficient of education was 4.187; this implies that a unit increase in education level is
expected to result in an increase in an individual’s prestige by 4.187.
The coefficient of income was found to be 0.001; this this implies that a unit increase in income
is expected to result in an increase in an individual’s prestige by 0.001.
R codes
Assignment2<-read.csv("C:\\Users\\310187796\\Desktop\\Assignment2.csv")
str(Assignment2)
summary(Assignment2)
library(pastecs)

stat.desc(Assignment2)
library(psych)
describe(Assignment2)
library(car)
par(mfrow=c(2,2))
y1 <- Assignment2$y1
h<-hist(y1, breaks=10, col="red", xlab="Class",
main="Histogram for y1")
xfit<-seq(min(y1),max(y1),length=40)
yfit<-dnorm(xfit,mean=mean(y1),sd=sd(y1))
yfit <- yfit*diff(h$mids[1:2])*length(y1)
lines(xfit, yfit, col="blue", lwd=2)
y2 <- Assignment2$y2
h<-hist(y2, breaks=10, col="green", xlab="Class",
main="Histogram for y2")
xfit<-seq(min(y2),max(y2),length=40)
yfit<-dnorm(xfit,mean=mean(y2),sd=sd(y2))
yfit <- yfit*diff(h$mids[1:2])*length(y2)
lines(xfit, yfit, col="blue", lwd=2)
y3 <- Assignment2$y3
h<-hist(y3, breaks=10, col="aquamarine", xlab="Class",
main="Histogram for y3")
xfit<-seq(min(y3),max(y3),length=40)
yfit<-dnorm(xfit,mean=mean(y3),sd=sd(y3))
yfit <- yfit*diff(h$mids[1:2])*length(y3)
lines(xfit, yfit, col="blue", lwd=2)
y4 <- Assignment2$y4
h<-hist(y4, breaks=10, col="blanchedalmond", xlab="Class",
main="Histogram for y4")
xfit<-seq(min(y4),max(y4),length=40)
yfit<-dnorm(xfit,mean=mean(y4),sd=sd(y4))
yfit <- yfit*diff(h$mids[1:2])*length(y4)
lines(xfit, yfit, col="blue", lwd=2)
par(mfrow=c(1,1))
y5 <- Assignment2$y5
h<-hist(y5, breaks=10, col="darkorchid", xlab="Class",
main="Histogram for y5")
xfit<-seq(min(y5),max(y5),length=40)
yfit<-dnorm(xfit,mean=mean(y5),sd=sd(y5))
yfit <- yfit*diff(h$mids[1:2])*length(y5)
lines(xfit, yfit, col="blue", lwd=2)
par(mfrow=c(2,2))
x1 <- Assignment2$x1

h<-hist(x1, breaks=10, col="darkolivegreen1", xlab="Class",
main="Histogram for x1")
xfit<-seq(min(x1),max(x1),length=40)
yfit<-dnorm(xfit,mean=mean(x1),sd=sd(x1))
yfit <- yfit*diff(h$mids[1:2])*length(x1)
lines(xfit, yfit, col="red", lwd=2)
x2 <- Assignment2$x2
h<-hist(x2, breaks=10, col="gold4", xlab="Class",
main="Histogram for x2")
xfit<-seq(min(x2),max(x2),length=40)
yfit<-dnorm(xfit,mean=mean(x2),sd=sd(x2))
yfit <- yfit*diff(h$mids[1:2])*length(x2)
lines(xfit, yfit, col="red", lwd=2)
x3 <- Assignment2$x3
h<-hist(x3, breaks=10, col="deeppink", xlab="Class",
main="Histogram for x3")
xfit<-seq(min(x3),max(x3),length=40)
yfit<-dnorm(xfit,mean=mean(x3),sd=sd(x3))
yfit <- yfit*diff(h$mids[1:2])*length(x3)
lines(xfit, yfit, col="red", lwd=2)
x4 <- Assignment2$x4
h<-hist(x4, breaks=10, col="gray", xlab="Class",
main="Histogram for x4")
xfit<-seq(min(x4),max(x4),length=40)
yfit<-dnorm(xfit,mean=mean(x4),sd=sd(x4))
yfit <- yfit*diff(h$mids[1:2])*length(x4)
lines(xfit, yfit, col="red", lwd=2)
par(mfrow=c(1,1))
x5 <- Assignment2$x5
h<-hist(x5, breaks=10, col="green1", xlab="Class",
main="Histogram for x5")
xfit<-seq(min(x5),max(x5),length=40)
yfit<-dnorm(xfit,mean=mean(x5),sd=sd(x5))
yfit <- yfit*diff(h$mids[1:2])*length(x5)
lines(xfit, yfit, col="red", lwd=2)
fit1 <- lm(y1 ~ x1 + x2 + x3, data=Assignment2)
summary(fit1)
# Assessing Outliers
outlierTest(fit1) # Bonferonni p-value for most extreme obs
qqPlot(fit1, main="QQ Plot") #qq plot for studentized resid
leveragePlots(fit1) # leverage plots

# Normality of Residuals
# qq plot for studentized resid
qqPlot(fit, main="QQ Plot")
# distribution of studentized residuals
library(MASS)
sresid <- studres(fit1)
hist(sresid, freq=FALSE,
main="Distribution of Studentized Residuals")
xfit<-seq(min(sresid),max(sresid),length=40)
yfit<-dnorm(xfit)
lines(xfit, yfit)
# Evaluate homoscedasticity
# non-constant error variance test
ncvTest(fit1)
# plot studentized residuals vs. fitted values
spreadLevelPlot(fit1)
# Evaluate Collinearity
vif(fit1) # variance inflation factors
sqrt(vif(fit1)) > 2 # problem?
# Evaluate Nonlinearity
# component + residual plot
crPlots(fit1)
# Ceres plots
ceresPlots(fit1)
fit2 <- lm(y2 ~ x1 + x2 + x3, data=Assignment2)
summary(fit2)
# Assessing Outliers
outlierTest(fit2) # Bonferonni p-value for most extreme obs
qqPlot(fit1, main="QQ Plot") #qq plot for studentized resid
leveragePlots(fit2) # leverage plots
# Normality of Residuals
# qq plot for studentized resid
qqPlot(fit2, main="QQ Plot")
# distribution of studentized residuals
library(MASS)
sresid <- studres(fit2)
hist(sresid, freq=FALSE,
main="Distribution of Studentized Residuals")
xfit<-seq(min(sresid),max(sresid),length=40)
yfit<-dnorm(xfit)
lines(xfit, yfit)

# Evaluate homoscedasticity
# non-constant error variance test
ncvTest(fit2)
# plot studentized residuals vs. fitted values
spreadLevelPlot(fit2)
# Evaluate Collinearity
vif(fit2) # variance inflation factors
sqrt(vif(fit2)) > 2 # problem?
# Evaluate Nonlinearity
# component + residual plot
crPlots(fit2)
# Ceres plots
ceresPlots(fit2)
fit3 <- lm(y3 ~ x1 + x2 + x3, data=Assignment2)
summary(fit3)
# Assessing Outliers
outlierTest(fit3) # Bonferonni p-value for most extreme obs
qqPlot(fit1, main="QQ Plot") #qq plot for studentized resid
leveragePlots(fit3) # leverage plots
# Normality of Residuals
# qq plot for studentized resid
qqPlot(fit3, main="QQ Plot")
# distribution of studentized residuals
library(MASS)
sresid <- studres(fit3)
hist(sresid, freq=FALSE,
main="Distribution of Studentized Residuals")
xfit<-seq(min(sresid),max(sresid),length=40)
yfit<-dnorm(xfit)
lines(xfit, yfit)
# Evaluate homoscedasticity
# non-constant error variance test
ncvTest(fit3)
# plot studentized residuals vs. fitted values
spreadLevelPlot(fit3)
# Evaluate Collinearity
vif(fit3) # variance inflation factors
sqrt(vif(fit3)) > 2 # problem?
# Evaluate Nonlinearity

# component + residual plot
crPlots(fit3)
# Ceres plots
ceresPlots(fit3)
fit4 <- lm(y4 ~ x4 + x5, data=Assignment2)
summary(fit4)
# Assessing Outliers
outlierTest(fit4) # Bonferonni p-value for most extreme obs
qqPlot(fit4, main="QQ Plot") #qq plot for studentized resid
leveragePlots(fit4) # leverage plots
# Normality of Residuals
# qq plot for studentized resid
qqPlot(fit4, main="QQ Plot")
# distribution of studentized residuals
library(MASS)
sresid <- studres(fit4)
hist(sresid, freq=FALSE,
main="Distribution of Studentized Residuals")
xfit<-seq(min(sresid),max(sresid),length=40)
yfit<-dnorm(xfit)
lines(xfit, yfit)
# Evaluate homoscedasticity
# non-constant error variance test
ncvTest(fit4)
# plot studentized residuals vs. fitted values
spreadLevelPlot(fit4)
# Evaluate Collinearity
vif(fit4) # variance inflation factors
sqrt(vif(fit4)) > 2 # problem?
# Evaluate Nonlinearity
# component + residual plot
crPlots(fit4)
# Ceres plots
ceresPlots(fit4)
fit5 <- lm(y5 ~ x5, data=Assignment2)
summary(fit5)
# Assessing Outliers
outlierTest(fit5) # Bonferonni p-value for most extreme obs

qqPlot(fit5, main="QQ Plot") #qq plot for studentized resid
leveragePlots(fit5) # leverage plots
# Normality of Residuals
# qq plot for studentized resid
qqPlot(fit4, main="QQ Plot")
# distribution of studentized residuals
library(MASS)
sresid <- studres(fit5)
hist(sresid, freq=FALSE,
main="Distribution of Studentized Residuals")
xfit<-seq(min(sresid),max(sresid),length=40)
yfit<-dnorm(xfit)
lines(xfit, yfit)
# Evaluate homoscedasticity
# non-constant error variance test
ncvTest(fit5)
# plot studentized residuals vs. fitted values
spreadLevelPlot(fit5)
# Evaluate Collinearity
vif(fit5) # variance inflation factors
sqrt(vif(fit5)) > 2 # problem?
# Evaluate Nonlinearity
# component + residual plot
crPlots(fit5)
# Ceres plots
ceresPlots(fit5)
Prestige<-read.csv("C:\\Users\\310187796\\Desktop\\prestige.csv")
str(Prestige)
myvars <- c("education", "income", "women", "prestige")
Prestige_new <- Prestige[myvars]
pairs(~education+income+women+prestige,data=Prestige_new,
main="Scatterplot Matrix")
describe(Prestige_new)
model1 <- lm(prestige ~ education, data=Prestige_new)
summary(model1)
model2 <- lm(prestige ~ income, data=Prestige_new)
summary(model2)
model3 <- lm(prestige ~ women, data=Prestige_new)
summary(model3)