Statistical Analysis of Blood Pressure, Sports, and Car Sales Data
VerifiedAdded on 2023/01/11
|4
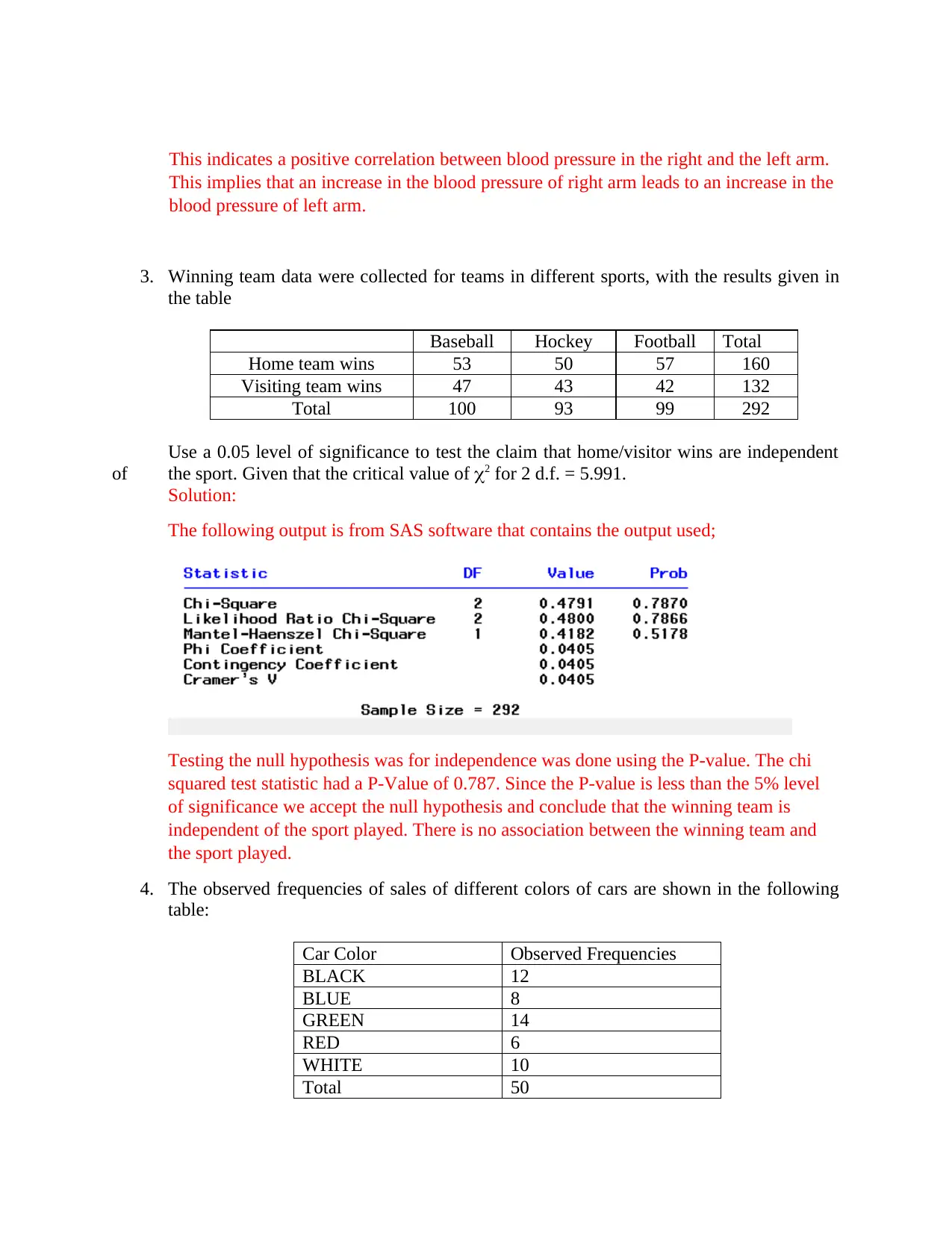
|970
|46
Homework Assignment
AI Summary
This statistics assignment provides detailed solutions to several problems. The first problem involves finding the predicted systolic blood pressure in the left arm using a regression line, given the systolic blood pressure in the right arm. The second problem calculates the linear correlation coefficient between blood pressures in the right and left arms. The third problem uses a chi-squared test to determine if home/visitor wins are independent of the sport played. The fourth problem calculates a chi-squared test statistic to assess if car sales of different colors have equal probabilities. The fifth problem constructs an ANOVA table and calculates the F-value for a one-way ANOVA. The final problem involves finding the F-test statistic value given sample data.
1 out of 4




![[object Object]](/_next/static/media/star-bottom.7253800d.svg)