Reservoir Rock Permeability Measurement and Analysis Report

This assignment is a comprehensive lab report on permeability measurement, a crucial property in reservoir engineering. The report details the experimental procedure for measuring permeability using gas flow through core samples, including setup, calibration, and data collection. It explains the application of Darcy's law and the Klinkenberg effect to account for gas slippage. The results section presents calculations of permeability, mean pressure, and the Klinkenberg constant. The discussion analyzes the obtained permeability value, its implications, and potential sources of error. The report also answers specific questions related to permeability, the influence of different fluids, and the comparison of theoretical and experimental values for the Klinkenberg constant. The report concludes with a summary of findings and references relevant literature.

PERMEABILITY MEASUREMENT
By Name
Course
Instructor
Institution
Location
Date

Introduction
Permeability is a fundamental reservoir rock property and is extremely important for
the reservoir engineers to determine during exploration of a well and obtain flow
characteristics of the reservoir. Permeability is ability of rock to conduct fluid. Higher
permeability means higher fluid flow in porous medium (Zimmermann et al., 2019, p.
501). Higher permeability means more effective (faster) recovery of Hydrocarbons.
Henry Darcy was a French engineer who formulated Darcy law based on the results of
the experiment on the flow of water through beds of sands, forming the basis of
hydrogeology. He was established that the flow rate is given by the equation below:
qα (h2−h 1)
L
OR
q= K (h 2−h1)
L
Where q = the volume of water crossing unit area in unit time.
L = the thickness of the sand.
h1 and h2 = The heights, above reference level, of the water in meters above and
below the sand respectively.
K = A factor of proportionality
This relationship evolved into what became as known as Darcy's law and has been
modified to the following:
q= K∗A∗∆ P
μL

Where:
q = flow rate of liquid cc/sec.
K = Permeability in Darcies.
A = Cross – sectional area of the core sample sq.cm.
∆ P = Differential pressure in bar.
L = Length of the core sample.
μ = Viscosity of flowing liquid, Centipoise.
Objective
To obtain the permeability of core samples by flowing gases through them and also
determine the "slip" or "Klinkenberg effect" by utilizing data from gas permeability
measurements.
Theory
Permeability of a rock defines a measure of the extent of ease of convection of fluids
through a rock and is determinable by a flow experiment. The flow rate of water flow
was determined by Henry Darcy in 1856 through a sand filter which may be described
using the equation
Q=KA/L (h1-h2)
Where Q is the volumetric flow rate through sand pack has a cross section area A and
length L with h1 and h2 being the hydrostatic heads at inlet and outlet of sand pack
respectively and K is a proportionality constant. These experiments were however

limited to water flow through sand packs that were 100% water saturated (He et al.,
2016).
Further investigations were later done that extent the study to other liquids in which
the constant of proportionality was replaced by k/ μ in which k defined the rock
permeability while μis the fluid viscosity of the fluid that flows through the rock. The
law would then be re-written as
Q=-kA/ μL*∆P
Where Q is given in cm3/s while k is the permeability as given in Darcy even as μ
defines the absolute viscosity in cP
Permeability tends to be inherent to the specific rock and is not a factor of the nature
of the used fluid in measuring it. The measurements of permeability were found to be
not constant on a core sample when gases are used as the fluid and instead changed
with the specific gas in making the measurement alongside average pressure that is
available in the core during the measurement time.
This experience examined the challenges faced when testing the permeability at
various flow rates through experimental analysis.
Procedure
1- Cylinder core plugs should be clean and dry perfectly, one inch in diameter and one
inch or less in length with parallel ends.
2- Check the system for leaks and calibrate the pressure transducer for pressure
transducer zeroing.
3- Connect the dry and clean nitrogen supply to the gas port.

4- The supply must have a regulator capable of supplying 25 psig to the supply port of
the unit.
5- Place the core plug to be tested in the core holder.
6- . Set the supply regulator to approximately 20 psig.
7- Open Valve V1 and adjust the flow pressure by rotating the handle of the
REGULATOR. Allow the UPSTREAM PRESSURE and the GAS FLOW RATE
displays to stabilize.
8- Record the stabilized upstream pressure and the temperature.
9- Increase the gas flow rate by rotating the regulator handle in a clockwise direction.
Again, allow the upstream pressure and the gas FLOW RATE displays to stabilize.
10- . Repeat the process at several upstream pressures to insure that the Darcian flow
is occurring. (The gas flow rate should increase linearly with increased flow pressure.)
11- . Enter the values of upstream pressure and flowrate with the permeability results
into Table (7-1).
Equation
Klinkenberg used the following relationship to obtain the slip effect of gases and
determined the permeability of liquid.
Kl= Kg
1+ b/ Pm
Where:
Kl = Permeability of non – reactive liquid.

Kg = Permeability of a gas.
Pm = mean pressure of flow.
b = Klinkenberg constant for a given gas in a given porous media.
Klinkenberg relationship can be also written as below:
Kg = Kl * b * (1/Pm) + Kl
Since gas (Nitrogen) which is compressible fluid flows through the core sample,
Darcy's equation for compressible fluids is modified to the following form which
allows measuring the permeability (Sander, Pan and Connell, 2017, p. 252):
Results
To calculate A = Pi * (D/2) ^2 = Pi * (6.45/2) ^2 = 11.46084 cm^2
To calculate Pm = (P1+P2)/2 = (2.021701 + 1.003333)/2 = 1.512517 atm and so on
To calculate 1/Pm = 1/1.512517 = 0.6611 atm^-1

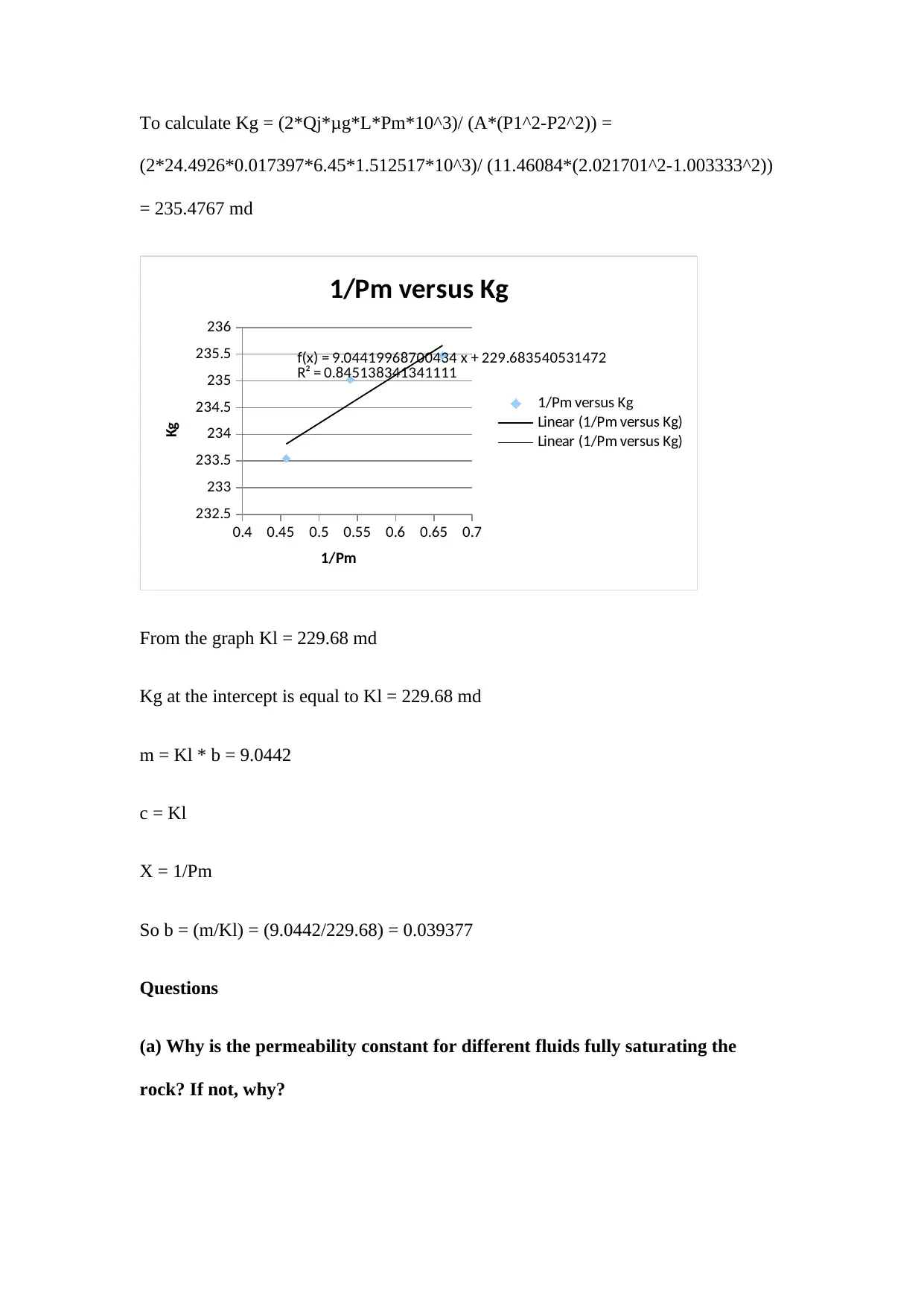
To calculate Kg = (2*Qj*μg*L*Pm*10^3)/ (A*(P1^2-P2^2)) =
(2*24.4926*0.017397*6.45*1.512517*10^3)/ (11.46084*(2.021701^2-1.003333^2))
= 235.4767 md
0.4 0.45 0.5 0.55 0.6 0.65 0.7
232.5
233
233.5
234
234.5
235
235.5
236
f(x) = 9.04419968700434 x + 229.683540531472
R² = 0.845138341341111
1/Pm versus Kg
1/Pm versus Kg
Linear (1/Pm versus Kg)
Linear (1/Pm versus Kg)
1/Pm
Kg
From the graph Kl = 229.68 md
Kg at the intercept is equal to Kl = 229.68 md
m = Kl * b = 9.0442
c = Kl
X = 1/Pm
So b = (m/Kl) = (9.0442/229.68) = 0.039377
Questions
(a) Why is the permeability constant for different fluids fully saturating the
rock? If not, why?

Since a fluid does not completely saturate a rock, there are other factors which come
in play apart from the distribution of the pore. Effective permeability is depend on the
dominant fluid saturation, characteristic of wettability, history of saturation as well as
geometry of pore (Lu et al., 2016, p.80)
(b) Value of b can be found from the slope m = Kl * b. Since you know m and Kl;
calculate b.
From the plot, m = Kl * b = 9.0442
Kl = 229.68 md
Then b = (m/Kl) = (9.0442/229.68) = 0.039377
(c) Klinkenberg showed that b = 0.777 Kl -o.39 compare the two values of b and
report the percentage difference assuming Klinkenberg value of b is true.
The theoretical value of b is higher than the experimental value of b. Experimental
studies are often associated with errors that may be from the instruments or even
human error hence the variation from the theoretical values.
% error=0.0568-0.03977/0.0568*100
=1.07%
Discussion
The value of permeability, k that was obtained from this study was 0.039377. The
value was obtained when the formula k=q/Ai was used. Prior to this the value of Ai
was initial determined and thereafter the value of q. Hence the permeability of the
sample can be considered to be moderate since the porosity of sand and gravel are
high or moderate in which water may flow through the soil with limited resistance. It

may drain easily even though it may hardly retain any water (He et al., 2016, p. 124)
The greater the size of a rock or substance, the more the permeability as compared to
rocks with small pore size. Form the calculated values of k, this rock may be
classified as silty or sand and may be said to be unrecommended for drainage system.
Conclusion
This was an experimental study on permeability of various substances. Permeability
was measured of various rocks and comparison made against the theoretical values
which was found to be different. The variation can be attributed to errors done during
the experiment including errors as a result of the apparatus or human errors. The
objectives of the experiment were attained in this study.

References
He, J., Ling, K., Pei, P. and Ni, X., 2016. Calculation of rock compressibility by using
the characteristics of downstream pressure change in permeability
experiment. Journal of Petroleum Science and Engineering, 143, pp.121-127
Lu, J., Nicot, J.P., Mickler, P.J., Ribeiro, L.H. and Darvari, R., 2016. Alteration of
Bakken reservoir rock during CO2-based fracturing—An autoclave reaction
experiment. Journal of Unconventional Oil and Gas Resources, 14, pp.72-85
Sander, R., Pan, Z. and Connell, L.D., 2017. Laboratory measurement of low
permeability unconventional gas reservoir rocks: A review of experimental
methods. Journal of Natural Gas Science and Engineering, 37, pp.248-279
Zimmermann, G., Zang, A., Stephansson, O., Klee, G. and Semiková, H., 2019.
Permeability enhancement and fracture development of hydraulic in situ experiments
in the Äspö hard rock laboratory, Sweden. Rock Mechanics and Rock
Engineering, 52(2), pp.495-515