Comparative Analysis: Holt Winters Model for Luck Stone Sales Forecast

This report aims to determine an optimal model for forecasting total sales data for Luck Stone as an alternative to their current regression model. The analysis applies 11 forecasting models to data collected from January 2013 to December 2017, with forecasts made from February 2017 to December 2017 to measure accuracy. The Holt Winters exponential smoothing model is highlighted for its simplicity, computational efficiency, adaptability, and accuracy. The model's performance is evaluated using MAE, MAPE, and RMSE. Results indicate that the Holt Winters model, with an alpha of 0.05 and a beta of 1.00, has a mean absolute error of 12.5%, lower than the existing regression model's 14%. The report concludes that the Holt Winters model is suitable for Luck Stone due to its lower prediction error, ability to incorporate new data, and better overall performance compared to other models.

Model
Forecasting
The aim of this study is solely based on the need to obtain an optimum model that optimally
forecasts total sales data Luck Stone which will be an alternative to the current model. From the
analysis, there are up to 11 forecasting models which have been applied on the data collected
between January 2013 and December 2017. All the forecasts are done from February 2017 to
December 2017 after which the accuracy of the forecasting models is measured.
In relation to the study objective, we use several statistics to compare between the models and
determine the optimum for application.
Holt Winters exponential smoothening
When presented with a discrete time series, there is a high probability that the analyst will at
some point consider use of a smoothening models in order to forecast the near future. Such is the
popularity of the smoothening forecast method making in probably the most used model in
forecast analyses (Ostertagova, 2011). The main factors underlying such wide adoption of the
model can be attributed to: the model’s simplicity, the efficiency of its computations, the ability
to adjust to new changes in the process of forecasting and its relatively good accuracy. Holt's
two-parameter model, which is alternatively referred to as linear exponential smoothing, is
among the most a popular smoothing model for forecasting data with trend. Ideally, Holt's model
includes three independent equations which work together for the generation of a final forecast.
In this analysis, we consider the use of Holt Winters exponential smoothening model (Jinka,
2018).
In application, the Holt Winters model uses exponential smoothing as mentioned above,

which is "used to reduce irregularities in time series data, thus providing a clearer view of the
true underlying behavior of the series. It also provides an effective means of predicting future
values of the time series” (Statistics Glossary, 2019).
The initial equation in the model is a basic smoothing equation which directly adjusts the last
smoothed value directly for the preceding time period trend. Holt’s model’s trend is updated over
time by models the second equation, in which the trend is defined as the difference in last two of
the smoothed value (Trubetskoy, 2016)s. Lastly is the third equation that generates the models
final forecast. As such, Holt's forecast model employs two parameters, where one is for its
overall smoothing while the other takes care of trend smoothing. Thus, this model is also known
as a “…double exponential smoothing or trend-enhanced exponential smoothing” (Kluwer
Academic Publishers, 2000).
The initial trend is estimated by:
Where y is the observation and L is the number of periods.
In Holt's model for forecasting, the performance is measured through conducting an evaluation
of: MAE (Mean Absolute Error), MAPE (Mean Absolute Percentage Error), alongside the
RMSE (Root Mean Square Error). After the optimal smoothing constant is obtained, then the
Holt’s model is applied to historical data for forecasting information for the succeeding year
(Nist , 2018).

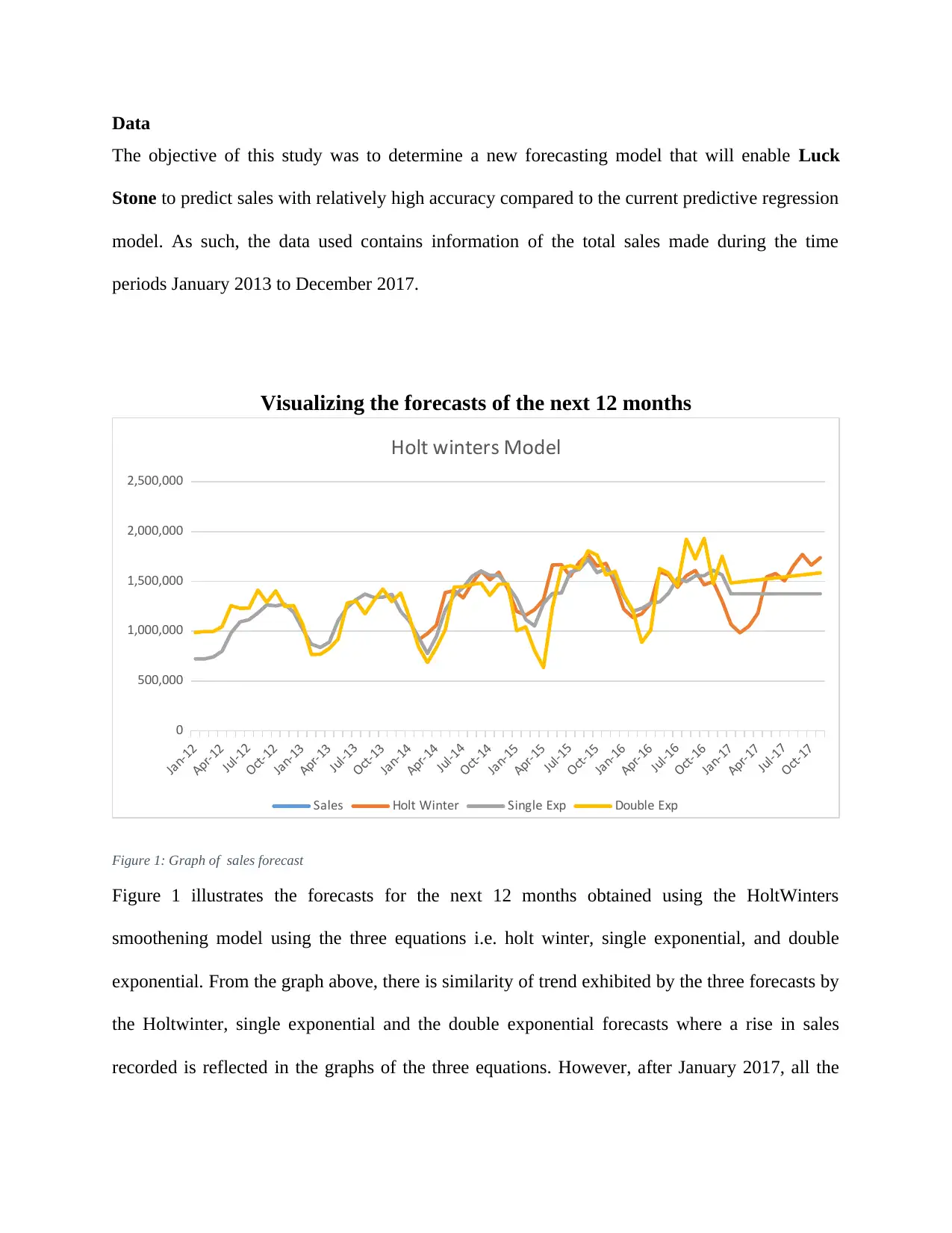
Data
The objective of this study was to determine a new forecasting model that will enable Luck
Stone to predict sales with relatively high accuracy compared to the current predictive regression
model. As such, the data used contains information of the total sales made during the time
periods January 2013 to December 2017.
Visualizing the forecasts of the next 12 months
Jan-12
Apr-12
Jul-12
Oct-12
Jan-13
Apr-13
Jul-13
Oct-13
Jan-14
Apr-14
Jul-14
Oct-14
Jan-15
Apr-15
Jul-15
Oct-15
Jan-16
Apr-16
Jul-16
Oct-16
Jan-17
Apr-17
Jul-17
Oct-17
0
500,000
1,000,000
1,500,000
2,000,000
2,500,000
Holt winters Model
Sales Holt Winter Single Exp Double Exp
Figure 1: Graph of sales forecast
Figure 1 illustrates the forecasts for the next 12 months obtained using the HoltWinters
smoothening model using the three equations i.e. holt winter, single exponential, and double
exponential. From the graph above, there is similarity of trend exhibited by the three forecasts by
the Holtwinter, single exponential and the double exponential forecasts where a rise in sales
recorded is reflected in the graphs of the three equations. However, after January 2017, all the

three equations indicate a dip in the total sales after which the Holt Winter model forecasts a rise
in sales which dips again in July. The double exponential which outputs the final forecast of the
Holt’s model indicates constant sales after the month of January 2017.
Performance measures of the Holt Winters Model
In the evaluation of performance measures as noted earlier, we consider statistics such as:
MAPE, MSE, MAE and RMSE which are given in table 1.
Alpha
0.05
Beta
1.00
Gamma
-
MAD 15
0,136
MAPE 12.5%
Figure 2: Performance metrics
In table 1, using an alpha of 0.05 and a beta of 1.00, the mean absolute error of the Holt winters
model is 12.5% which is relatively lower compared to the 14% mean absolute error recorded by
the current regression model. Considering the mean absolute deviation, the Holt’s model has the
lowest MAD compared to all other models except for the seasonalized monthly average at 3

moving average which however increase at 12 moving average thus indicating variability
depending on the moving average chosen.
Among models with single performance metrics such as the simple exponential smoothening
model etcetera, the Holt’s model has the least errors indicating better prediction and stability i.e.
it does not have different measure metrics for the same data.
Best
From among all the models that were suggested for consideration, the Holt Winters model has
the least means absolute error implying that it has the least error of prediction compared to the
other models hence suitable for use in the forecasting problem faced by Lucky Stone. In
addition, the model allows for entry of new data since as noted earlier, the models key strengths
include: its simplicity, efficiency of computations, the ability to adjust to new changes in the
process of forecasting and as seen a significantly good accuracy.
In this regard, we can propose for the adopting of the Holt Winters forecasting model to the
senior leadership as an alternative to the current linear regression model due to its relatively
better performance, ability to accept new data and forecast with lesser errors+++++++.

References
Jinka, P., 2018. Holt-Winters Forecasting Simplified. [Online]
Available at: https://www.vividcortex.com/blog/holt-winters-forecasting-simplified
[Accessed 11 May 2019].
Kluwer Academic Publishers, 2000. HOLT'S FORECASTING MODEL. 2000 edition ed. Boston:
Springer.
Nist , 2018. Triple Exponential Smoothing. In: Engineering Statistics handbook. Illinois: nist, pp.
72-76.
Ostertagova, E., 2011. THE SIMPLE EXPONENTIAL SMOOTHING MODEL. MODELLING
OF MECHANICAL AND MECHATRONIC SYSTEMS , 12 March, pp. 380-384.
Statistics Glossary, 2019. Time Series Data.. [Online]
Available at: http://www.stats.qla.ac.uk/steps/.qlossary/time series.html
[Accessed 10 May 2019].
Trubetskoy, G., 2016. Holt-Winters Forecasting for Dummies (or Developers) - Part I. [Online]
Available at: https://grisha.org/blog/2016/01/29/triple-exponential-smoothing-forecasting/
[Accessed 11 May 2019].