4-Axis SCARA-RRT Robot Forward Kinematics: DH Table and Solution

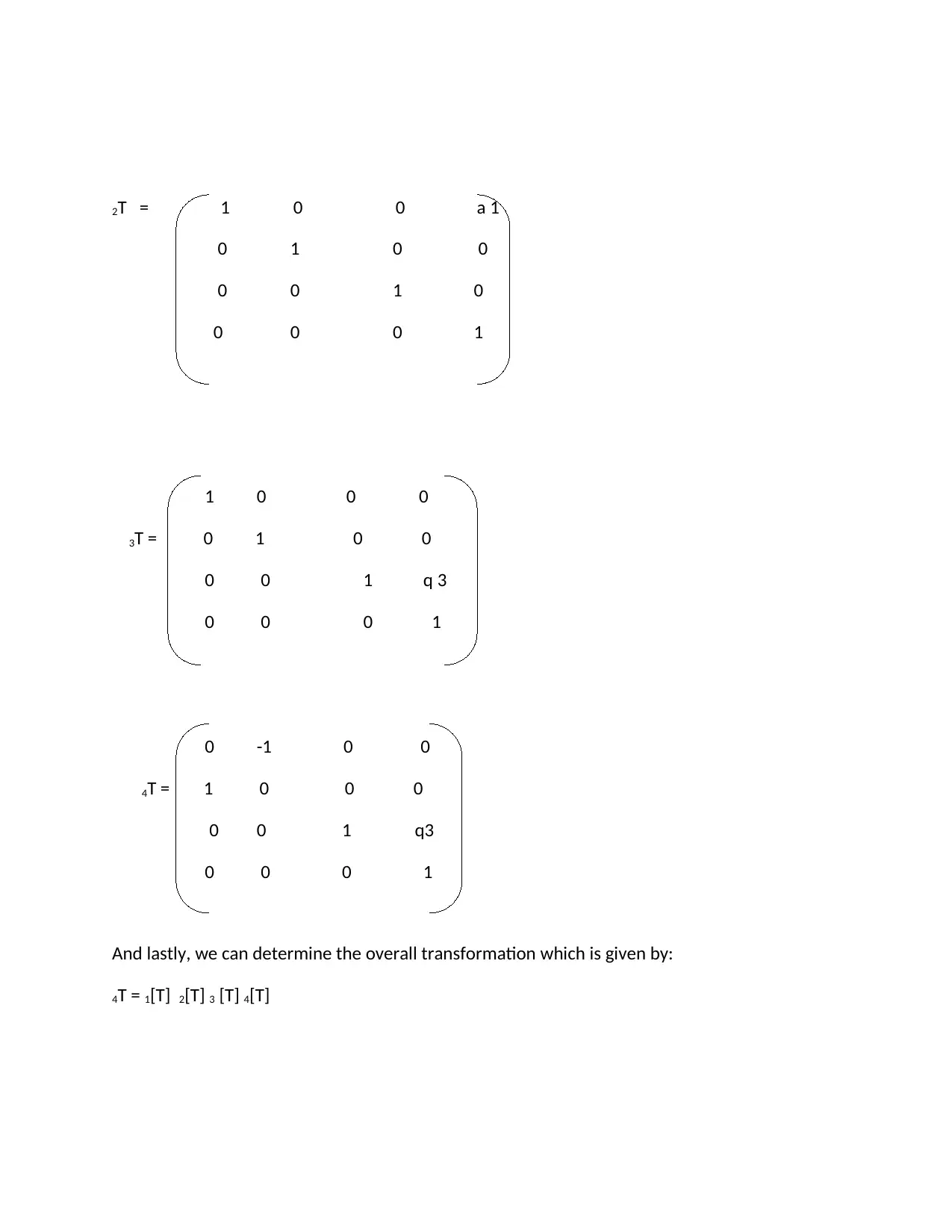
This assignment provides a comprehensive solution to the forward kinematics problem for a 4-axis SCARA-RRT robot. The solution begins by constructing the Denavit-Hartenberg (DH) table based on the robot's joint orientations and given parameters. The homogenous transformation matrices for each joint are then derived using the DH parameters. By multiplying these individual transformation matrices, the overall transformation matrix is obtained, which relates the tool tip position to the base coordinate system. Finally, the position of the tool tip is deduced from the overall transformation matrix, and the arm equations are combined to provide a complete kinematic description of the robot. This detailed solution allows for the determination of the tool's position in space based on the robot's joint variables.

SOLUTION TO THE ASSIGNMENT
QN 1: To determine the position of the tooltip, first of all, we will fill the DH table appropriately
based on the Joints orientation and the given parameters.
Table 1: The DH Table
Axis (i) α θ A d S C
1 π 0 a 1 d 0 1
2 0 0 a 2 0 0 1
3 0 0 0 q 3 0 1
4 0 0.5π 0 q 3 1 0
Now, it should be noted that:
S= Sin (q) and C= Cos(q)
Therefore Sin (0)= 0, Sin(0.5π)= 1, Cos(0)= 1 and Cos(0.5π)=0
The homogenous transform can be obtained from tables and the given matrix below:
i-1T = Cθi -Sθi 0 ai-1
SθiCά-1 CθiCά-1 -Sά-1 -diSά-1
SΘiSά-1 CθiSά-1 Cά-1 diCά-1
0 0 0 1
The simplified form of matrix can be used in this case for each joint ( that is from joints 1 to 4):
1 0 0 0
1T = 0 -1 0 0
0 0 -1 d
0 0 0 1

2T = 1 0 0 a 1
0 1 0 0
0 0 1 0
0 0 0 1
1 0 0 0
3T = 0 1 0 0
0 0 1 q 3
0 0 0 1
0 -1 0 0
4T = 1 0 0 0
0 0 1 q3
0 0 0 1
And lastly, we can determine the overall transformation which is given by:
4T = 1[T] 2[T] 3 [T] 4[T]

Therefore multiplying the above transformations yield:
1 0 0 a2 0 -1 0 0
0 -1 0 0 x 1 0 0 0
0 0 -1 d 0 0 1 2q3
0 0 0 1 0 0 0 1
0 -1 0 a2
= -1 0 0 0
0 0 -1 d-2q3
0 0 0 1
Qn 2: Hence the position of the tool tip can be deduced from the matrix above:
P(q) = a2
0
d-2q3

Qn 3: The arm equation :
x= a2
y= 0
Z= d-2q3
Combining these equations yields: X+y+z = d-2q3+a2