MATH 2711 Assignment 5 Solution: Green's Theorem and Surface Integrals

This document presents a comprehensive solution to MATH 2711 Assignment 5, focusing on several variable calculus. The solution begins by verifying Green's Theorem by calculating the circulation of a vector field around a closed curve using both line integrals and double integrals. The solution then proceeds to prove the identity div(∇f × ∇g) = 0, where f and g are scalar functions. Finally, the assignment calculates the surface area integral over a portion of a sphere defined by the plane z = R. The solutions are detailed, including parametric equations, step-by-step calculations, and clear explanations, making it a valuable resource for students studying multivariable calculus.

Answer
The given vector field is:
F = hP, Qi = h−y2, x2i
Circulation of a vector field around a closed curve C,by Green’s Theorem,
is given as: I
C
P dx + Q dy =
ZZ
D
Qx − Py dA
where, C is oriented counter-clockwise and D is the region enclosed by C.
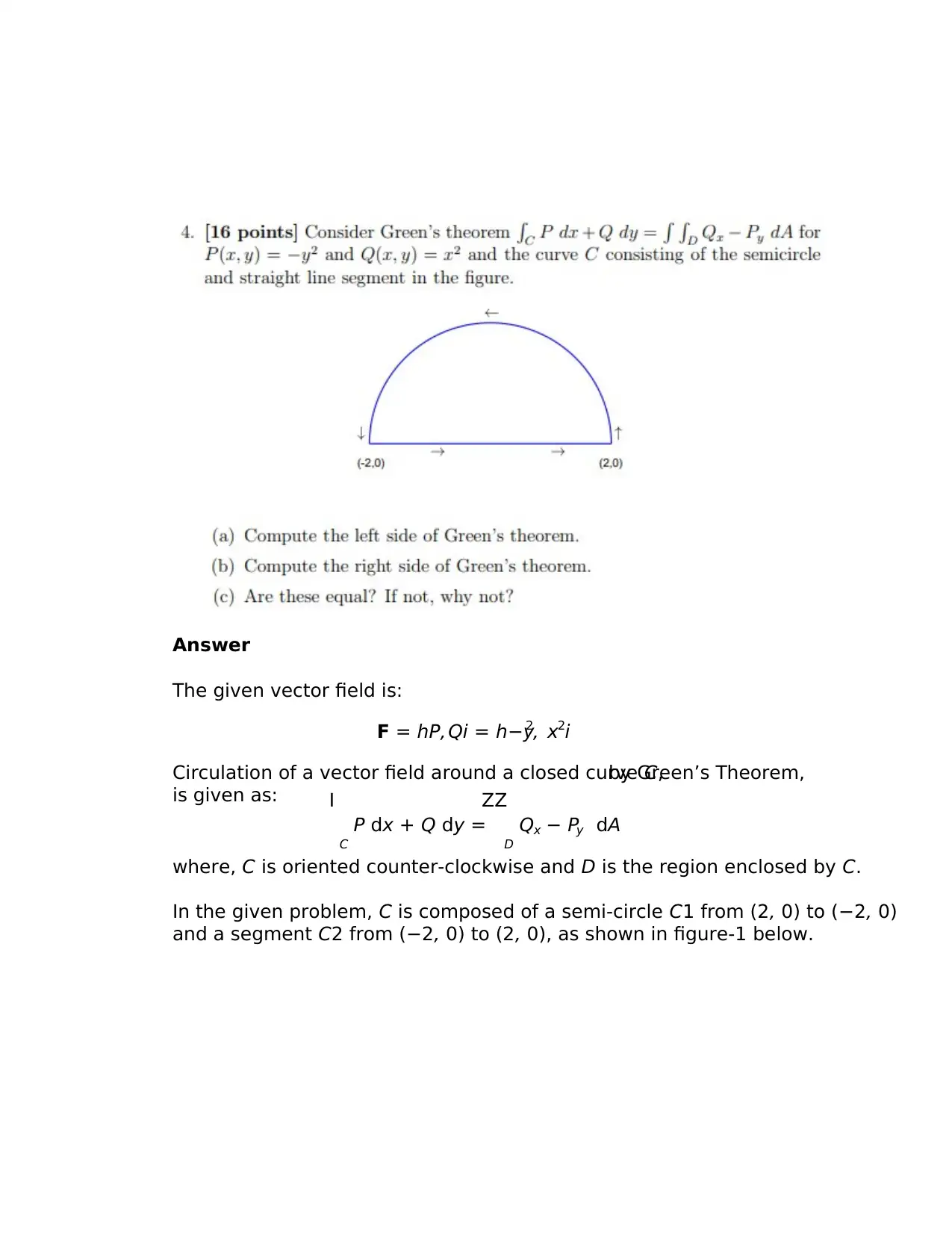
In the given problem, C is composed of a semi-circle C1 from (2, 0) to (−2, 0)
and a segment C2 from (−2, 0) to (2, 0), as shown in figure-1 below.

Figure 1:Path of integral (C)
a) Left side of Green’s Theorem:
Using the property of line integrals, circulation is calculated as:
I
C
P dx + Q dy =
Z
C1
P dx + Q dy +
Z
C2
P dx + Q dy
In order to evaluate these line integrals, we need to first define the parametric
equations for curve C1 and C2.
Path C1: from (2, 0) to (−2, 0)
It is a semi-circle centered at origin with radius=2.Therefore,
r(t) = h2 cos t,2 sin t [0 ≤ t ≤ π]
Implies, dr = h−2 sin t,2 cos ti dt
Therefore,
Z
C1
P dx + Q dy =
Z
C1
hP, Qi · dr
=
Z
C1
h−y2, x2i · h−2 sin t,2 cos ti dt
[Put: y = 2 sin t,x = 2 cos t]
=
Z
C1
h−4 sin2 t, 4 cos2 ti · h−2 sin t,2 cos ti dt
=
Z
C1
8 sin3 t + 8 cos3 t dt

[0 ≤ t ≤ π]
=
Z π
0
8 sin3 t + 8 cos3 t dt
[Trig. Identity:sin3 x = 3
4 sin x −
1
4 sin 3x]
[Trig. Identity:cos3 x = 3
4 cos x +
1
4 cos 3x]
= 8
Z π
0
3
4 sin t −
1
4 sin 3t +
3
4 cos t +
1
4 cos 3t dt
= 8 −3
4 cos t +
cos 3t
12 + 3
4 sin t +
sin 3t
12
π
0
= 8 3
2 − 1
6 + 0 + 0= 32
3
Path C2: from (−2, 0) to (2, 0)
It is straight line connecting two points along the x- axis.Therefore,
r(t) = ht, 0i [−2 ≤ t ≤ 2]
Implies, dr = h1, 0i dt Therefore,
Z
C2
P dx + Q dy =
Z
C2
hP, Qi · dr
=
Z
C2
h−y2, x2i · h1,0i dt

[Put: y = 0,x = t]
=
Z
C2
h0,t2i · h1,0i dt
=
Z
C2
0 dt = 0
Therefore, I
C
P dx + Q dy =32
3 + 0 =32
3
b) Right side of Green’s Theorem:
We have,
P = −y2 & Q = x2
Therefore,
Qx = ∂
∂x (x2) = 2x
Py = ∂
∂y(−y2) = −2y
Double integral from Green’s Theorem:
ZZ
D
Qx − Py dA =
ZZ
D
2x + 2y dA
In order to evaluate the double integralinside the semi-circle D,we will
switch to polar co-ordinates.Semi-circle is centered at origin with radius =
2. Therefore,
x = r cos θ,y = r sin θ
Also, dA = rdrdθ.Limits of integration in D are:
r : 0 ≤ r ≤ 2 & θ : 0 ≤ θ ≤ π

Therefore,
ZZ
D
2x + 2y dA =
ZZ
D
2r cos θ + 2r sin θrdrdθ
=
Z π
0
Z 2
0
2r2 cos θ + 2r2 sin θ drdθ
=
Z π
0
h2r3
3 cos θ +
2r3
3 sin θ
i 2
0
dθ
=
Z π
0
16
3 cos θ +
16
3 sin θ dθ
= 16
3 sin θ −
16
3 cos θ
π
0
= 0 +32
3 = 32
3
c)
Yes, both are equal.Hence, Green’s Theorem is verified.
Answer
To prove:
div(∇f × ∇g) = 0

where, f and g are two (scalar) functions and ∇f and ∇g gives their gradient,
respectively.
Step 1) First let us verify the formula for divergence of cross products of two
vectors A and B:
div(A × B) = B(∇ × A) − A(∇ × B) (1)
A = hA1, A2, A3i
B = hB1, B2, B3i
By definition of cross product:
A × B = (A2B3 − A3B2), (A3B1 − A1B3), (A1B2 − B1A2)
Taking divergence:
div(A × B) = ∂
∂x (A2B3 − A3B2), ∂
∂y(A3B1 − A1B3), ∂
∂z (A1B2 − B1A2)
(2)
Now, curl ofA is:
∇ × A = ∂
∂yA3 − ∂
∂z A2 , ∂
∂z A1 − ∂
∂x A3 , ∂
∂x A2 − ∂
∂yA1
Therefore,
B(∇ × A) = B1
∂
∂yA3 − ∂
∂z A2 + B2
∂
∂z A1 − ∂
∂x A3 + B3
∂
∂x A2 − ∂
∂yA1
(3)
Similarly,
∇ × B = ∂
∂yB3 − ∂
∂z B2 , ∂
∂z B1 − ∂
∂x B3 , ∂
∂x B2 − ∂
∂yB1
Therefore,
A(∇ × B) = A1
∂
∂yB3 − ∂
∂z B2 + A2
∂
∂z B1 − ∂
∂x B3 + A3
∂
∂x B2 − ∂
∂yB1
(4)

Subtract (4) from (3) and compare with each term from (2), for example:
∂
∂x A2B3 = A2
∂
∂x B3 + B3
∂
∂x A2
Examining each term, we find that the identity holds.
Therefore, we conclude:
div(A × B) = B(∇ × A) − A(∇ × B)
Step 2) Curl of a gradient is zero:
Curl of a vector F is defined as:
∇ × F = ∂
∂yF3 − ∂
∂z F2 , ∂
∂z F1 − ∂
∂x F3 , ∂
∂x F2 − ∂
∂yF1
Let F be a gradient field, such that F = ∇f .Therefore,
hF1, F2, F3i = ∂f
∂x , ∂f
∂y , ∂f
∂z
Therefore,
∇×F = ∇×(∇f) = ∂2f
∂y∂z − ∂2f
∂z∂y , ∂2f
∂z∂x − ∂2f
∂x∂z , ∂2f
∂x∂y − ∂2f
∂y∂x
If f is differential-able in the given domain, then the mixed partial derivatives
of second order are equal, that is:
∂2f
∂z∂x = ∂2f
∂x∂z
and so on.Therefore, each term of the curl becomes zero, hence:
∇ × (∇f) = 0
Step 3)
We have to calculate:
div(∇f × ∇g)
Using identity (2) :
div(∇f × ∇g) = ∇g(∇ × ∇f) − ∇f(∇ × ∇g)

But in Step 2), we got:∇ × ∇g = ∇ × ∇g = 0.Therefore,
div(∇f × ∇g) = ∇g(0) − ∇f(0) = 0
Hence proved.
Answer
S is part of a sphere,in plane z = R, centered at origin with radius =
R.
Parametric equation for the sphere is given as:
r(φ, θ) = hR sin φ cos θ,R sin φ sin θ,R+R cos φi [0 ≤ φ ≤ π/2,0 ≤ θ ≤ 2π]
Therefore,
rθ = h−R sin φ sin θ,R sin φ cos θ,0i
rφ = hR cos φ cos θ,R cos φ sin θ, −R sin φi
Now,
rθ × rφ =
ˆi ˆj ˆk
−R sin φ sin θR sin φ cos θ 0
R cos φ cos θR cos φ sin θ−R sin φ
= h−R2 sin2 φ cos θ, −R2 sin2 φ sin θ, −(R2 sin φ cos φ(sin2 θ + cos2 θ)i
= h−R2 sin2 φ cos θ, −R2 sin2 φ sin θ, −R2 sin φ cos φ i

Therefore,
||rθ × rφ|| =
q
R4 sin4 φ cos2 θ + R4 sin4 φ sin2 θ + R4 sin2 φ cos2 φ
= R2 sin φ
q
sin2 φ cos2 θ + sin2 φ sin2 θ + cos2 φ
= R2 sin φ
Surface area element in parametric form is given as:
dS = ||rθ × rφ|| dφdθ
Therefore,
ZZ
S
z2 dS =
Z 2π
0
Z π/2
0
(R + R cos φ)2 R2 sin φdφdθ
=
Z 2π
0
Z π/2
0
R4 sin φ + R4 cos2 φ sin φ + 2R4 cos φ sin φdφdθ
= R4
Z 2π
0
h
− cos φ −
1
3 cos3 φ + sin2 φ
i π/2
0
dθ
= R4
Z 2π
0
7
3 dθ
= 14πR4
3
References :
1. Stewart, J. (2016).Single variable calculus.Boston, MA: Cengage Learn-
ing.