MATLAB Simulink Design of a Ship Roll Stabilization System

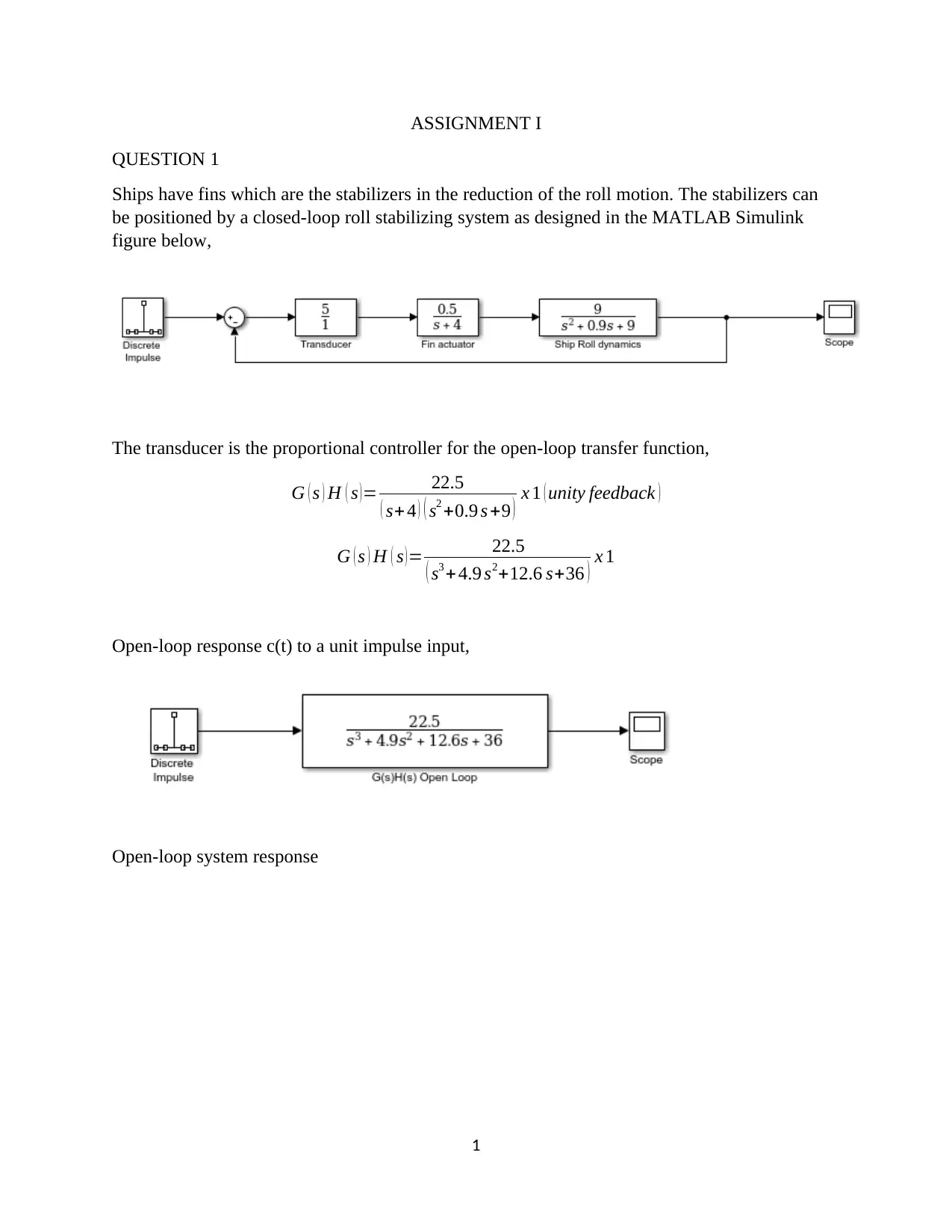
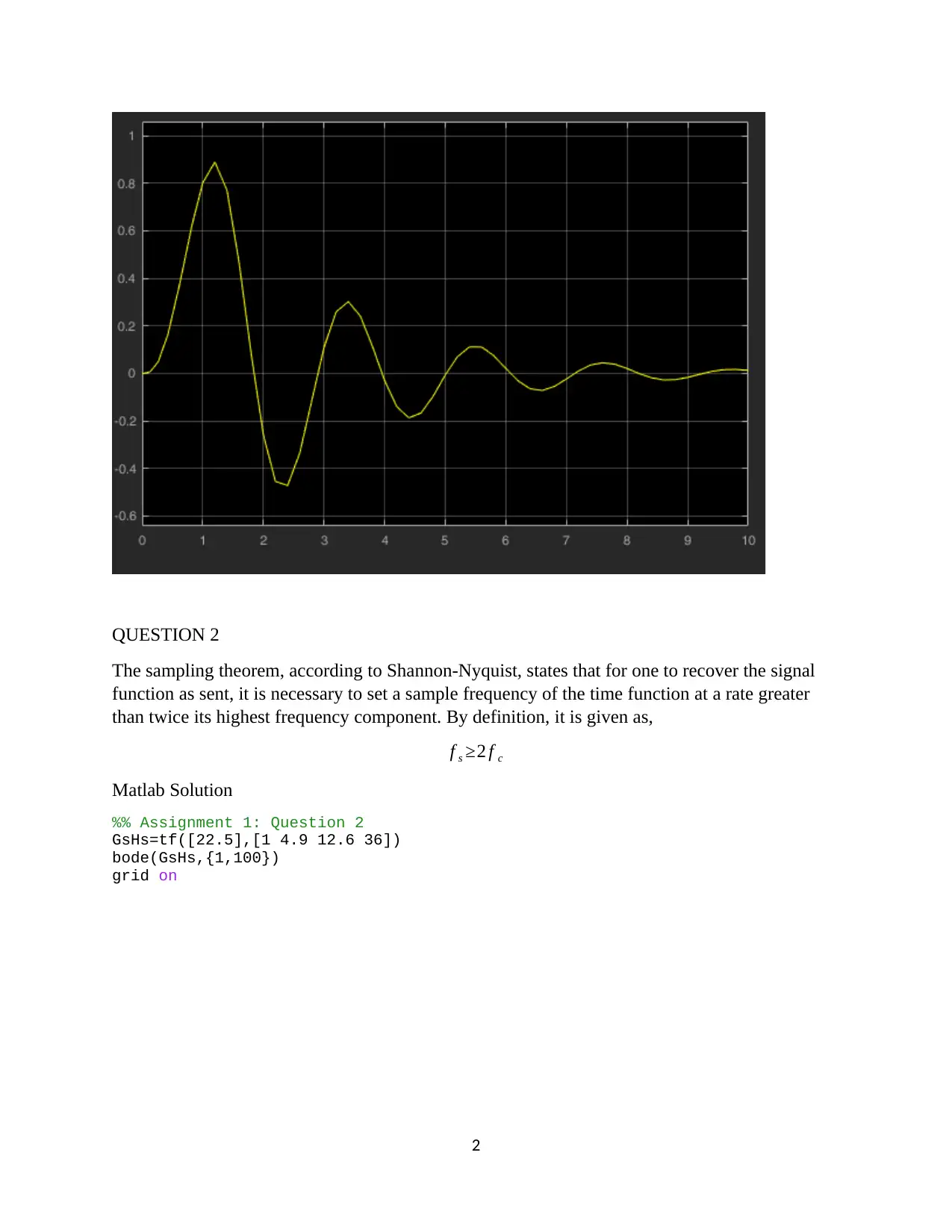
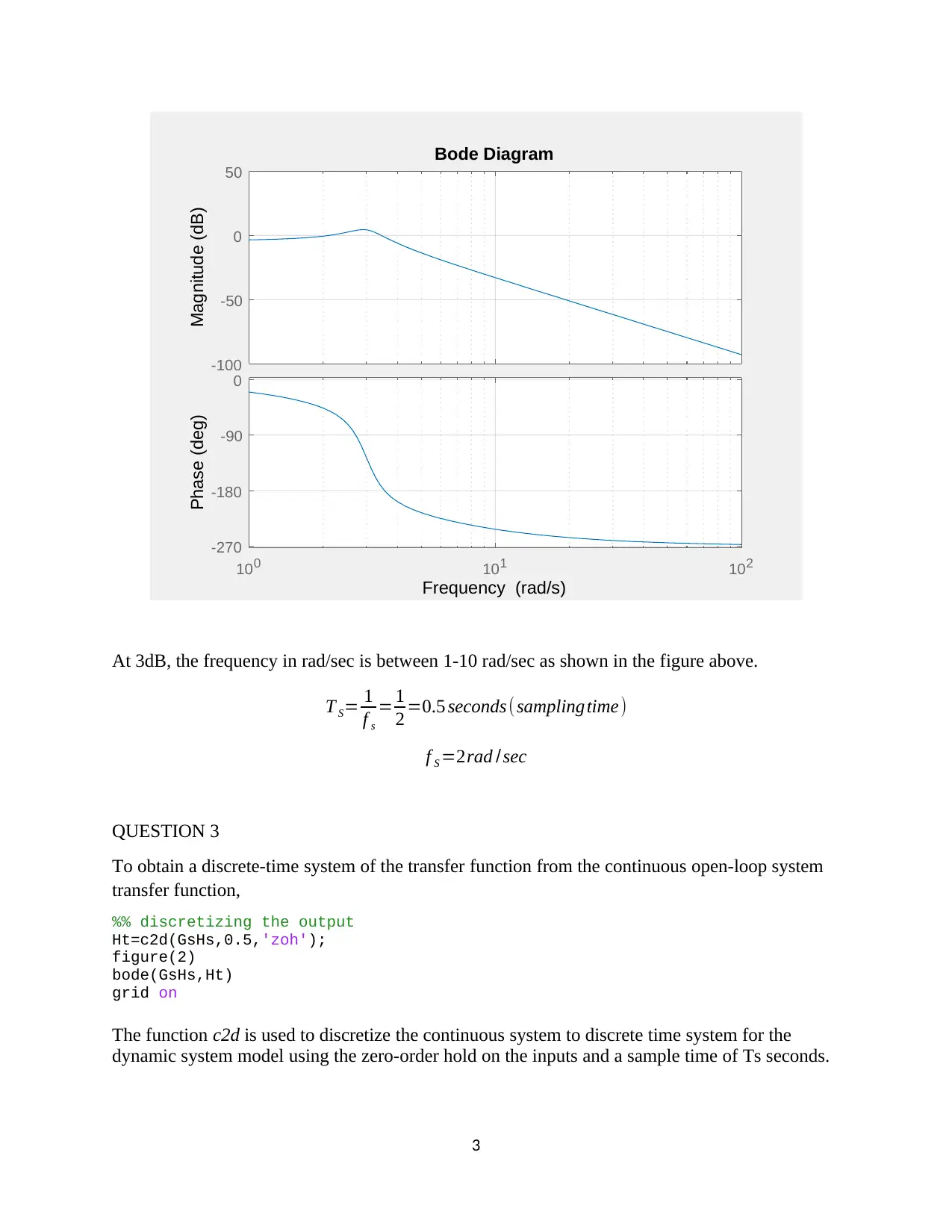
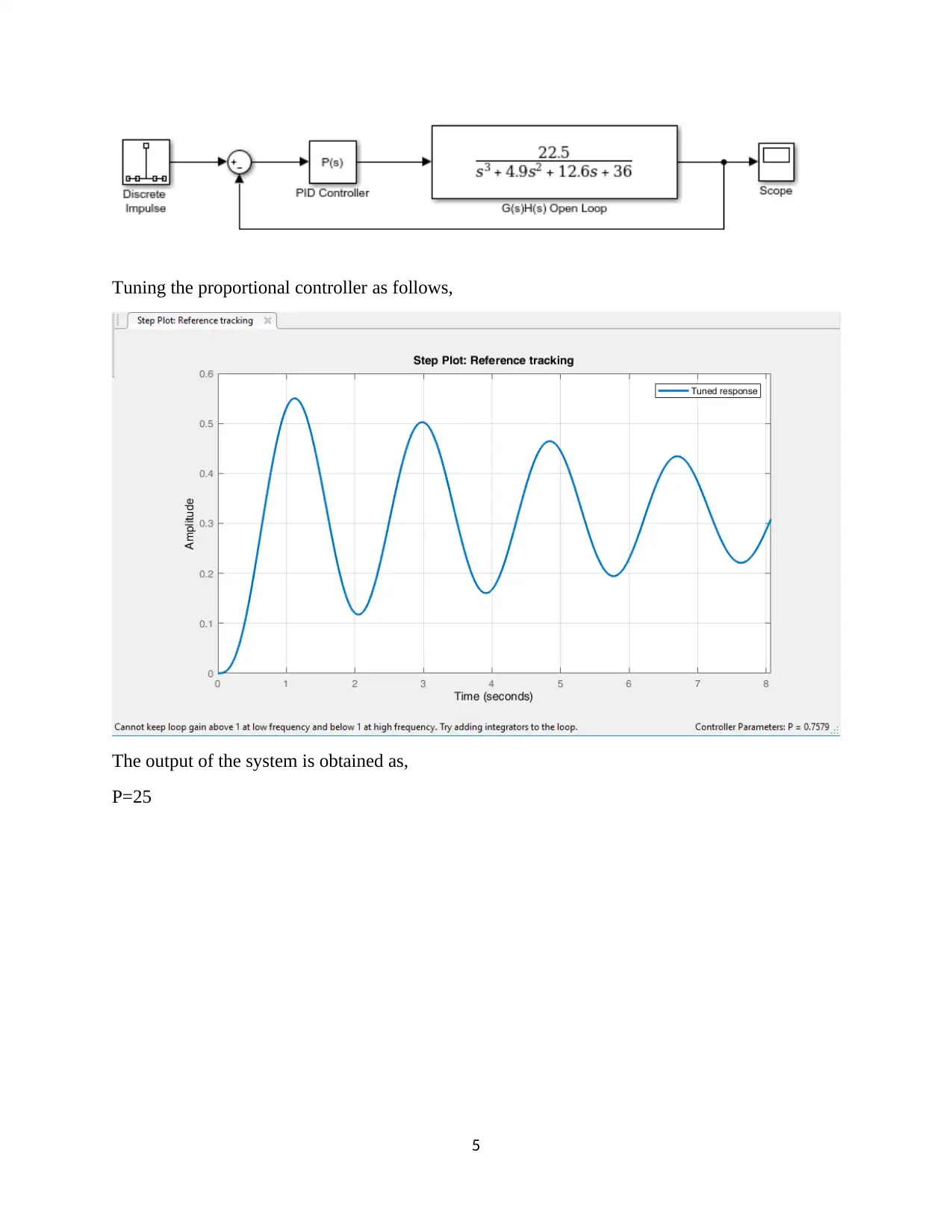
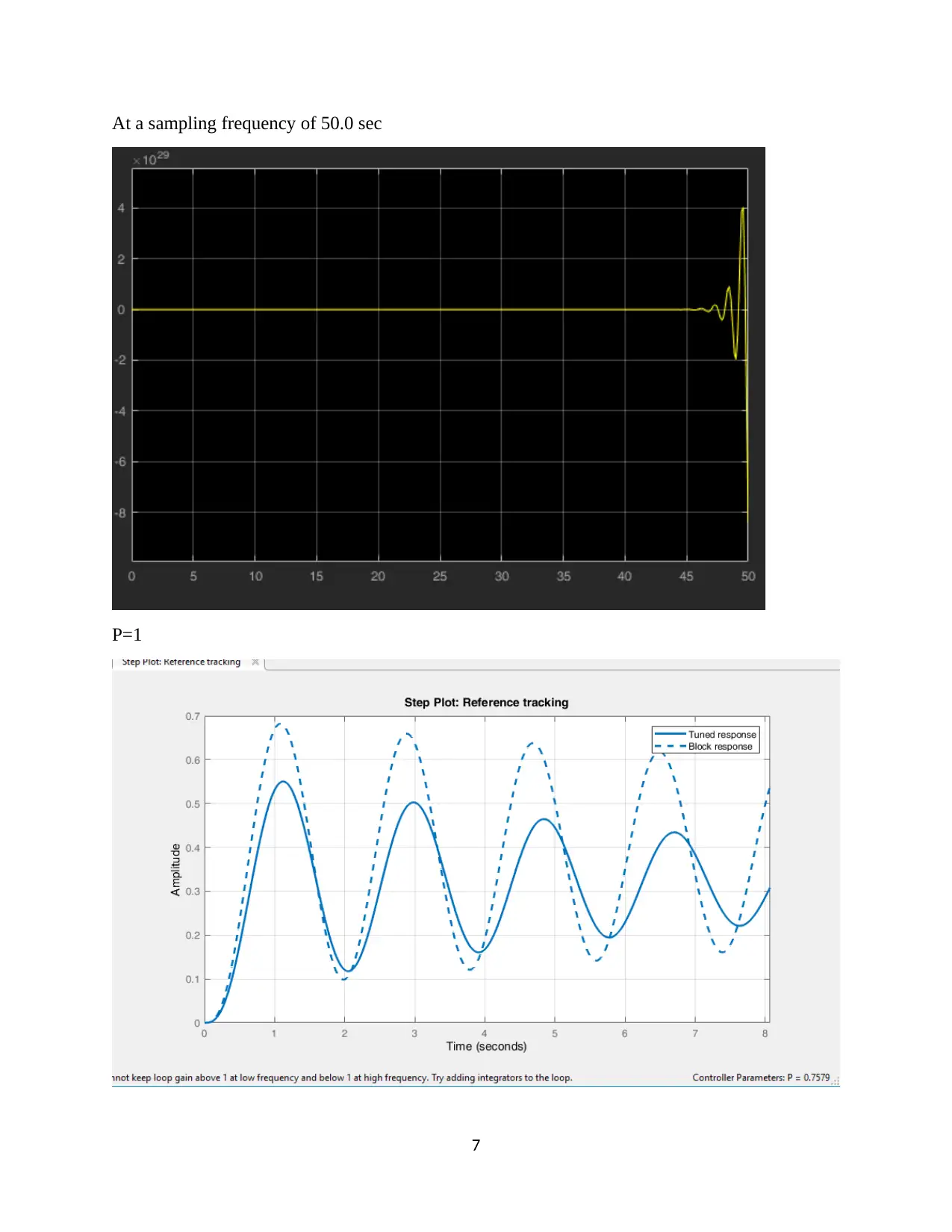
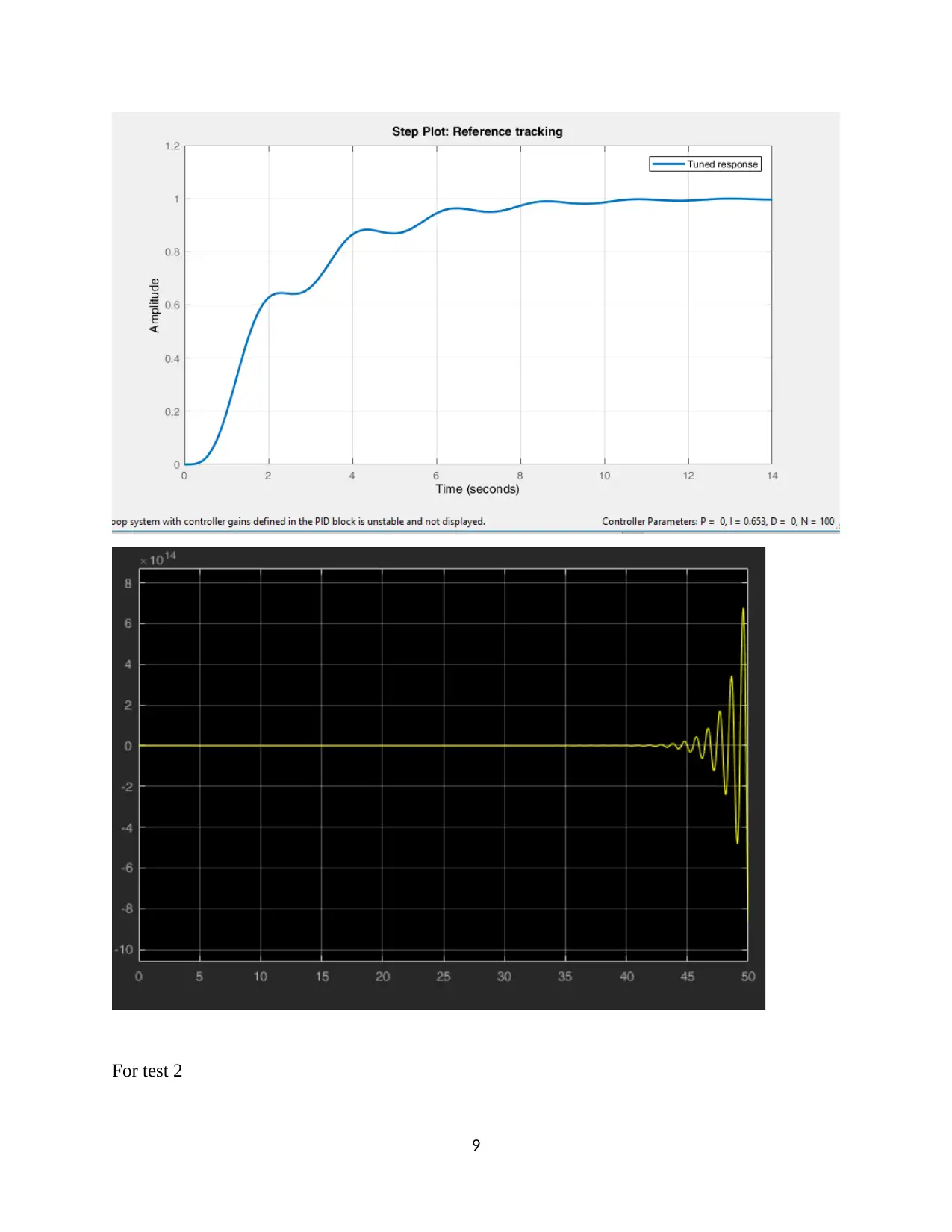
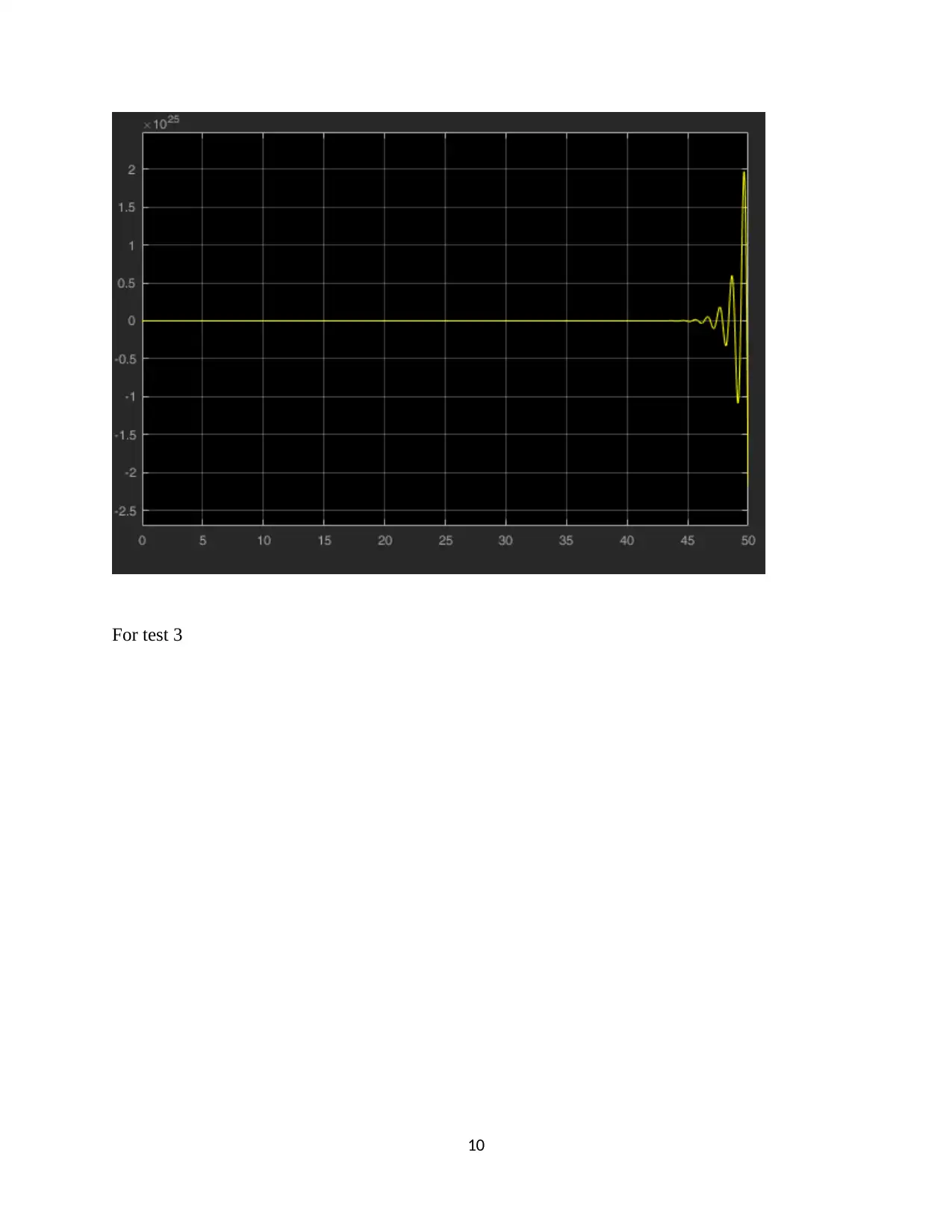
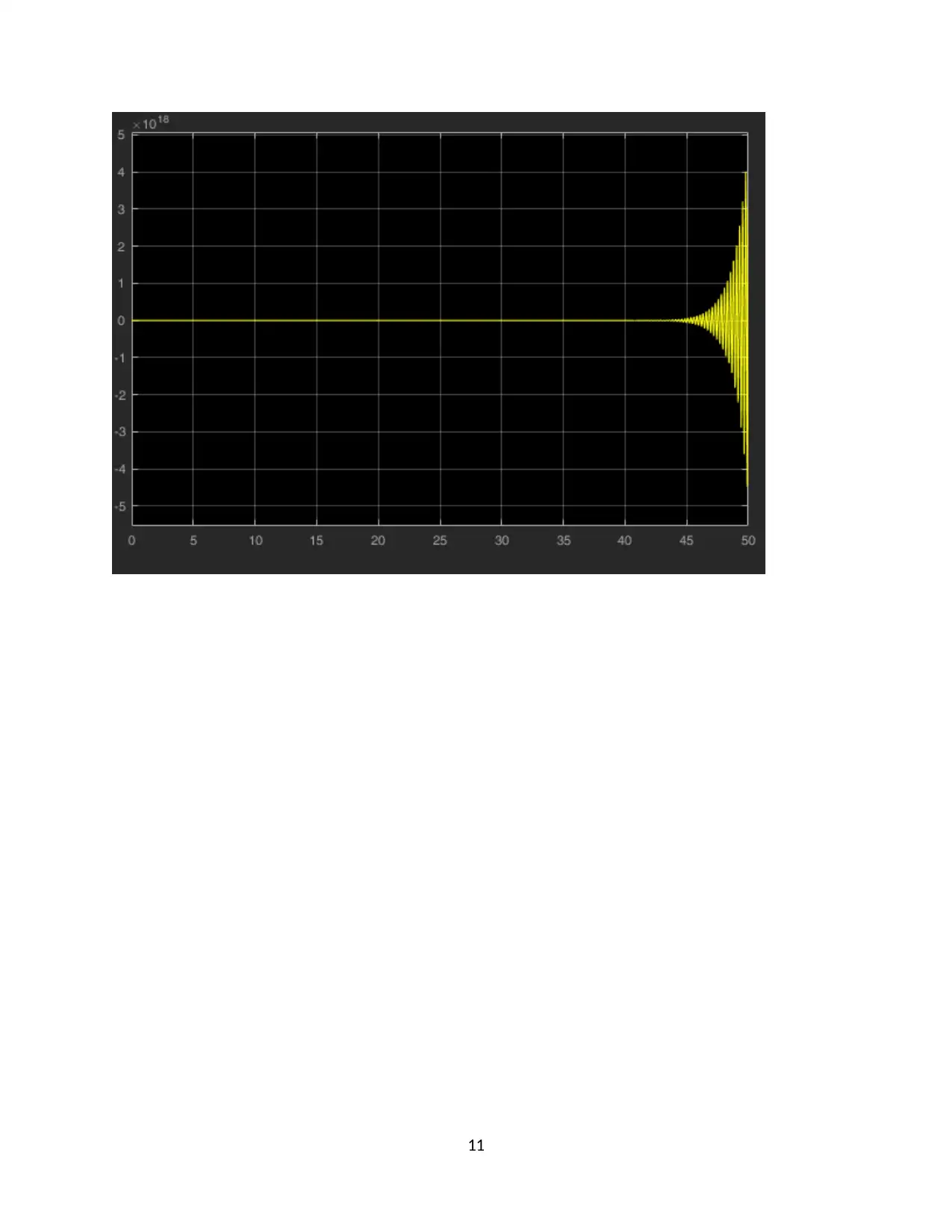
This assignment focuses on the design and analysis of a closed-loop roll stabilizing system for ships using digital control methods and MATLAB Simulink. The first question involves finding the open-loop response to a unit impulse input. The second question determines a suitable sample interval based on the sampling theorem and Bode plots. The third question derives the discrete-time system transfer function. The fourth question designs a digital proportional controller, and the fifth replaces it with a PID controller, tuning parameters for optimal performance. The second assignment involves designing a position control system with a power amplifier, motor, and load, simulating it in MATLAB, discretizing the system, selecting a proper sampling interval, designing a state variable feedback regulator, and implementing a dead-beat observer for state variable feedback. The solution provides detailed MATLAB code and simulation results for each part of the assignment.

UNIVERSITY AFFILIATION
FACULTY OR DEPARTMENT
COURSE ID & NAME
TITLE:
STUDENT NAME:
STUDENT REGISTRATION NUMBER:
PROFESSOR (TUTOR)
DATE OF SUBMISSION

ASSIGNMENT I
QUESTION 1
Ships have fins which are the stabilizers in the reduction of the roll motion. The stabilizers can
be positioned by a closed-loop roll stabilizing system as designed in the MATLAB Simulink
figure below,
The transducer is the proportional controller for the open-loop transfer function,
G ( s ) H ( s )= 22.5
( s+ 4 ) ( s2 +0.9 s +9 ) x 1 ( unity feedback )
G ( s ) H ( s ) = 22.5
( s3 + 4.9 s2+12.6 s+36 ) x 1
Open-loop response c(t) to a unit impulse input,
Open-loop system response
1

QUESTION 2
The sampling theorem, according to Shannon-Nyquist, states that for one to recover the signal
function as sent, it is necessary to set a sample frequency of the time function at a rate greater
than twice its highest frequency component. By definition, it is given as,
f s ≥2 f c
Matlab Solution
%% Assignment 1: Question 2
GsHs=tf([22.5],[1 4.9 12.6 36])
bode(GsHs,{1,100})
grid on
2

-100
-50
0
50
Magnitude (dB)
100 101 102
-270
-180
-90
0
Phase (deg)
Bode Diagram
Frequency (rad/s)
At 3dB, the frequency in rad/sec is between 1-10 rad/sec as shown in the figure above.
T S= 1
f s
= 1
2 =0.5 seconds( samplingtime)
f S =2rad /sec
QUESTION 3
To obtain a discrete-time system of the transfer function from the continuous open-loop system
transfer function,
%% discretizing the output
Ht=c2d(GsHs,0.5,'zoh');
figure(2)
bode(GsHs,Ht)
grid on
The function c2d is used to discretize the continuous system to discrete time system for the
dynamic system model using the zero-order hold on the inputs and a sample time of Ts seconds.
3

-100
-50
0
50
Magnitude (dB)
10-2 10-1 100 101 102
-360
-270
-180
-90
0
Phase (deg)
Bode Diagram
Frequency (rad/s)
Ht =
0.2384 z^2 + 0.4979 z + 0.07302
-------------------------------------
z^3 - 0.2753 z^2 + 0.6566 z - 0.08629
Sample time: 0.5 seconds
Discrete-time transfer function.
QUESTION 4
Designing the proportional control to form a unity feedback control system and optimize its
parameter P with respect to the performance criterion IAE using the steepest descent
minimization process.
4

Tuning the proportional controller as follows,
The output of the system is obtained as,
P=25
5

P=10
6

At a sampling frequency of 50.0 sec
P=1
7

QUESTION 5
Replacing the Proportional controller with a PID,
Using the table below to perform tests,
Test 1 Test 2 Test 3
Proportional (P) 10 10 10
Integral (I) 1 20 20
Derivative (D) 1 1 30
For test 1
8

For test 2
9

For test 3
10

11