SCMD Assignment 1: Analysis and Report on Shipping Cost Optimization

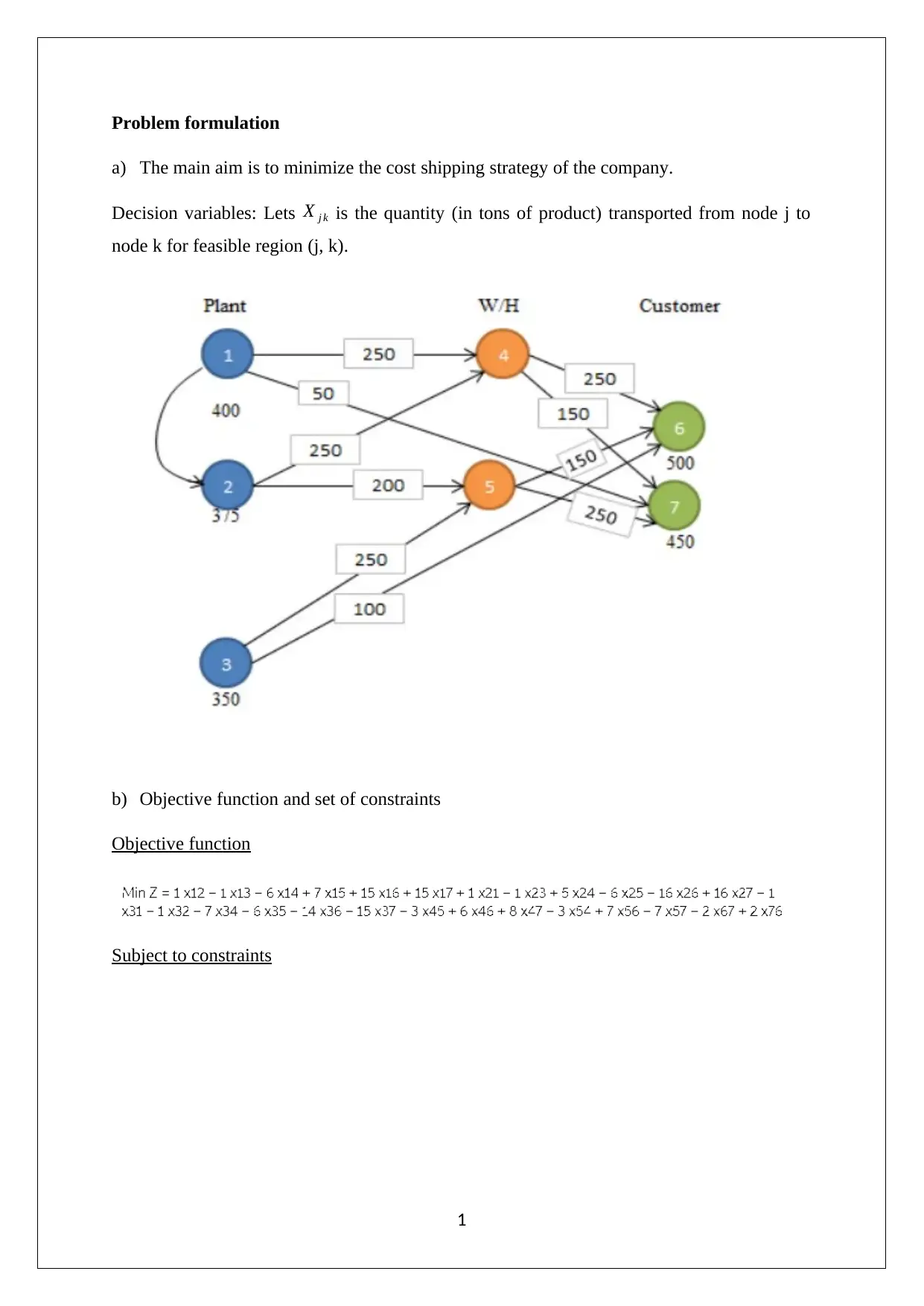
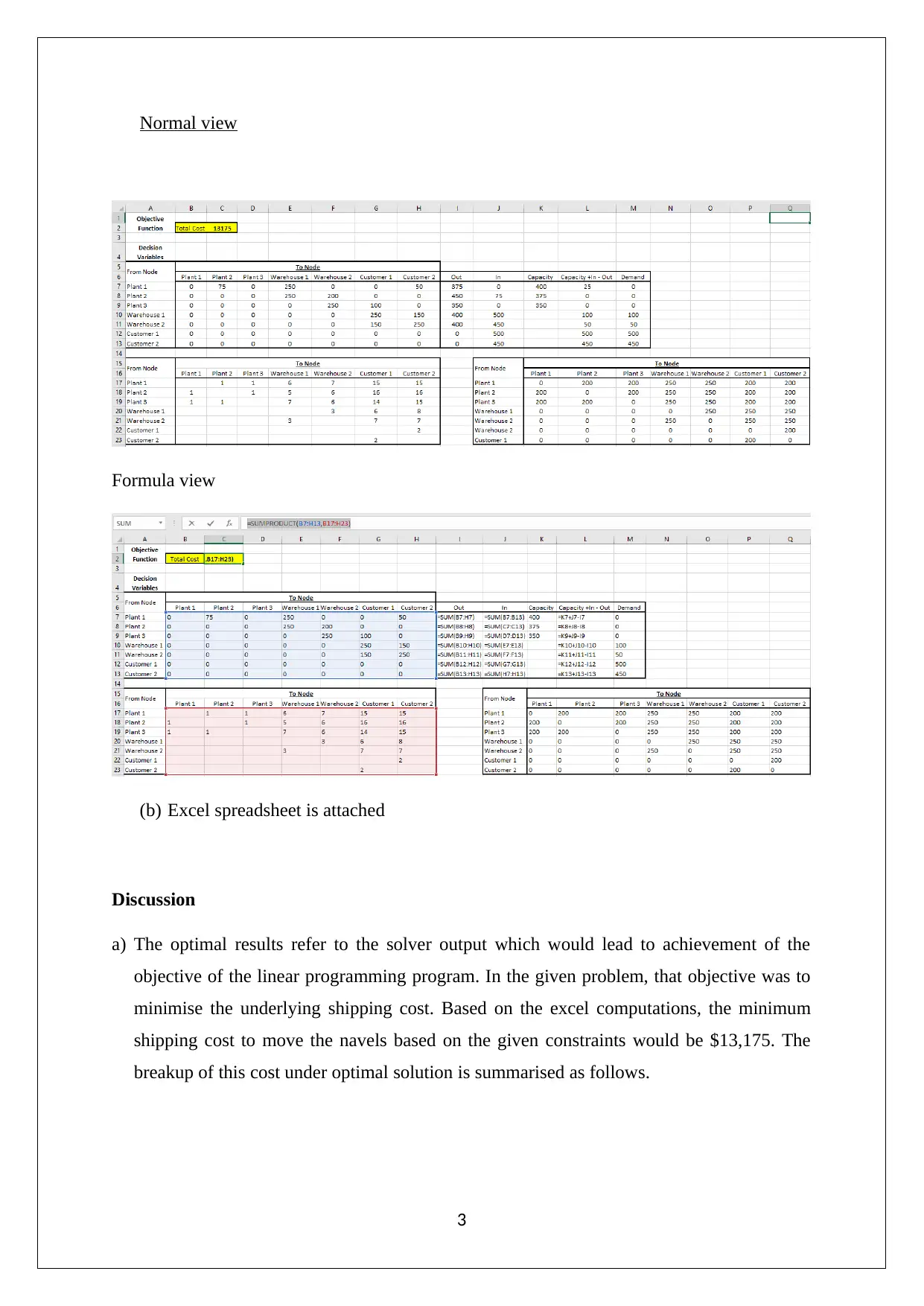
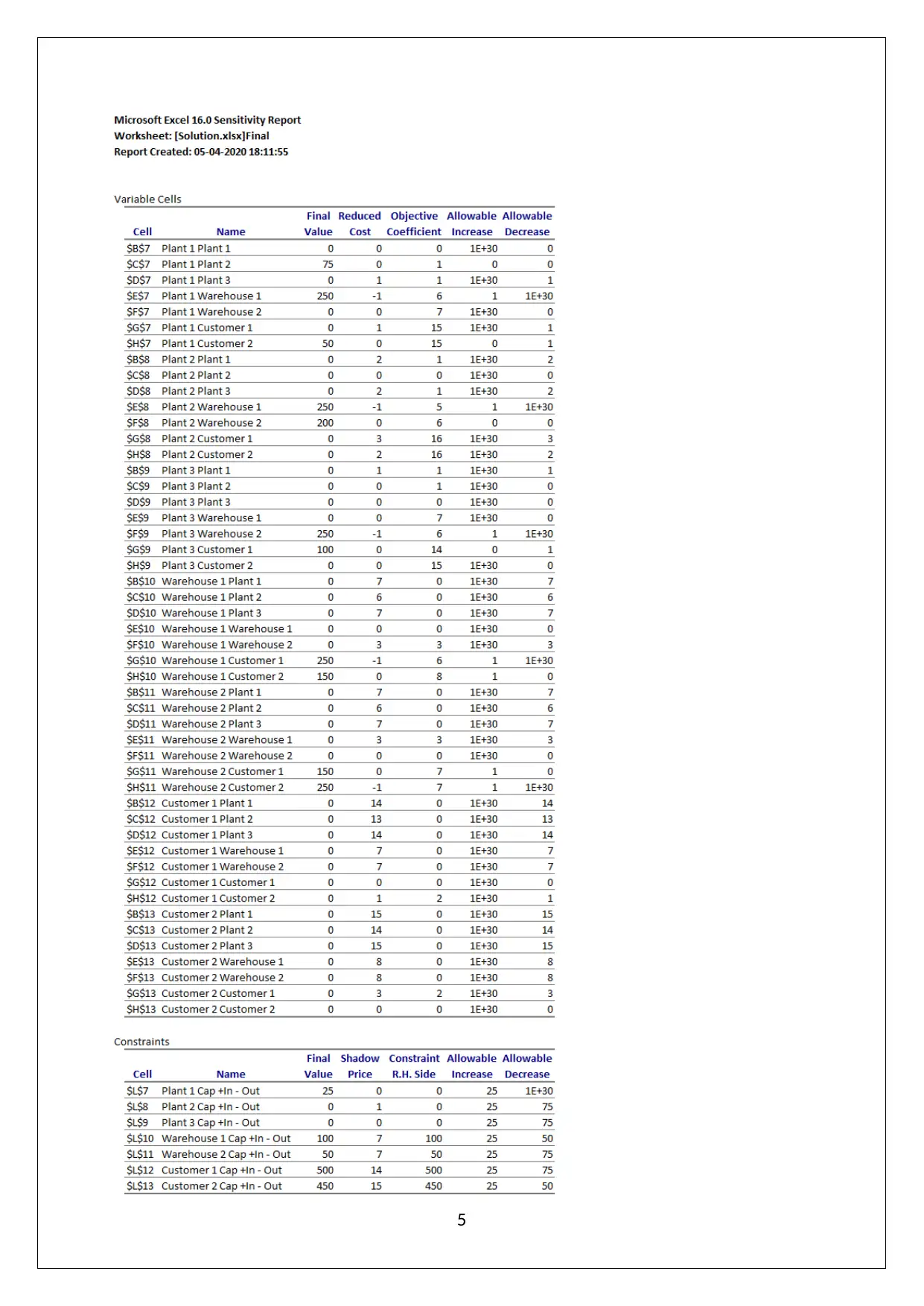
This report presents the solution to SCMD Assignment 1, focusing on minimizing shipping costs through the application of linear programming techniques. The assignment involves formulating a shipping strategy problem, defining decision variables, and establishing objective functions and constraints. The solution utilizes an Excel spreadsheet and Solver to determine the optimal flow of products between nodes, resulting in a minimized shipping cost of $13,175. The report includes a detailed sensitivity analysis, identifying the impact of changes in customer capacity on overall costs. Recommendations are provided to further reduce shipping costs by increasing specific plant capacities. The report provides insights into the problem formulation, solution methodology, and key findings, making it a valuable resource for understanding shipping cost optimization.

SCMD Assignment 1
Student Names & IDs
[DATE]
Report

Problem formulation
a) The main aim is to minimize the cost shipping strategy of the company.
Decision variables: Lets X j k is the quantity (in tons of product) transported from node j to
node k for feasible region (j, k).
b) Objective function and set of constraints
Objective function
Subject to constraints
1

c) Decision variables and linkage with the data
The decision variables have been used to determine the minimal shipping cost and the
optimal quantities of the product. The connection among the decision variables and the
requisite data have been shown in the excel spreadsheet.
Problem Solving
(a) & (b)
 Put the decision variable’s value zero
 Write the constraints after making references from decision variable’s value
 Write objective function corresponding to cost and decision variables
 Final used solver- add ins of excel to solve the linear programming problem through
simplex method after considering the non-negativity constraints
2

Normal view
Formula view
(b) Excel spreadsheet is attached
Discussion
a) The optimal results refer to the solver output which would lead to achievement of the
objective of the linear programming program. In the given problem, that objective was to
minimise the underlying shipping cost. Based on the excel computations, the minimum
shipping cost to move the navels based on the given constraints would be $13,175. The
breakup of this cost under optimal solution is summarised as follows.
3

b) The requisite sensitivity report for the given problem is as highlighted below.
4

5

From the constraints, it is apparent that the cost seems quite sensitive to capacity of both the
customers. If there is a one unit increase in the constraint related to customer 1 capacity, then
the cost can potentially decrease by $ 14. With regards to customer 2 capacity, the
corresponding value is $15. Also, from the variable cells, it is evident that the sensitivity of
the cost is not the same across the plants and customer. For instance, the highest sensitivity of
$ 15 is seen with regards to customer 2 plant 1 and customer 2 plant 3.
Recommendations
The appropriate flow of products between nodes for minimisation of the shipping costs as
determined through the solver is summarised as follows.
This is expected to result in shipping costs of $ 13,175.
Based on sensitivity analysis, it is recommended that the following need to be increased so as
to lower the shipping costs further.
 Customer 1 plant 1 capacity (Decrease by $ 14 per unit change)
 Customer 1 plant 2 capacity (Decrease by $ 13 per unit change)
 Customer 1 plant 3 capacity (Decrease by $ 14 per unit change)
 Customer 2 plant 1 capacity (Decrease by $ 15 per unit change)
 Customer 2 plant 2 capacity (Decrease by $ 14 per unit change)
 Customer 2 plant 3 capacity (Decrease by $ 15 per unit change)
6