Experiment: Measuring Gravitational Acceleration Using a Pendulum

This assignment details a physics experiment designed to calculate the gravitational acceleration (g) using a simple pendulum. The introduction explains the concept of gravity and gravitational acceleration, emphasizing its vector nature and typical value on Earth. The experiment involves measuring the time period of oscillation for a pendulum of varying lengths. The document includes a diagram of the experimental setup, assumptions, and the formula used (T = 2π√(l/g)). The procedure outlines the steps for the experiment, including setting up the pendulum, measuring the time for multiple oscillations, and calculating the time period and gravitational acceleration. The results are presented in a table and graph, analyzing the relationship between pendulum length and the square of the time period. The analysis compares the calculated value of g with the accepted value and discusses potential sources of error, such as the mass and flexibility of the string, air resistance, and limitations in measurement tools and human reaction time. The assignment concludes with references to support the findings and discussions. The percent error was calculated and the sources of error were discussed in detail.

Experiment
Measurement of gravitational acceleration (g) with the simple pendulum.
Aim: -
To calculate gravitational acceleration (g) with measurement of oscillation and time taken for
that oscillation of a simple pendulum.
Introduction:-
Any two objects which have some mass always tries to pull towards each other, this pulling
force simply known as gravity force. So simply anything which has their own mass also has
its gravitational pulling force. The gravitational force has directly proportional to the mass of
both objects so more mass means more gravity force on that. That’s the simple reason why
everything on earth which has mass is always feels attracted towards the centre of the earth.
The gravitational acceleration means the acceleration generated by the influence of the
gravitational pulling force. Acceleration due to gravity on earth usually denotes by ‘g’. Here,
acceleration is a vector quantity so it must have direction and magnitude both. Values
calculated from mass so it’s different for each different object, and direction is referred
towards a centre of mass of the body. So that gravity slows down the object moving away
from the centre of the planet earth or any other planet. And it also speeds up any objects
moving towards the centre of the earth. This gain or loss in the speed is steady and caused by
the force of the gravitational attraction N Suwanpayak et al (2018).
9.80665 m/s2 is accepted as a typical value of gravitational acceleration for the earth. The
direction of this is always towards the core of the earth. Moon has approximately 1/6th of the
acceleration from the earth. It is also changes on the surface of the earth like at sea level or in
deep caves (near to the centre of the earth) value of g is high compared to value on the Mount
Everest or another such high magnitude place. In addition to that earth is not a perfect sphere,
it’s like a spheroid due to that the value of g is greater on poles compare to the equator. On
earth, at different points gravitational acceleration varies from 9.764 m/s2 to 9.834 m/s2. So
every free-falling object attracts towards the core of the earth by acceleration g, simply it
means that its speed is increase by g m/s in each second.
A simple pendulum has described by a point mass hooked up by a weightless thread from one
fixed pivot point about which it can swing freely forward and backward in that place. For
point mass, it is best to use a small metal ball that has a higher mass and lesser diameter. The
back and forth motion of this metal ball towards pivot points are known as periodic motion or
oscillation. Time for one complete cycle like, Time taken by the ball to return back to one
end position is known as the time period (T) of oscillation.
When metal ball slightly displaced from its mean position, due to gravity there will be
restoring force generated which forces the pendulum to come back to its mean position. As
pendulum passes its mean position, the direction of forces will change and it tries to make it
in the equilibrium position.
1

Diagram:-
Below diagram shows an experimental setup of the simple pendulum system.
Description:-
Assumption:-
[1] Weight of the string is negligible compared to weight of the bob.
[2] Used thread must be inextensible, fully flexible and weight less.
[3] Pendulum length means distance between pivot points of string to centre of gravity of
the bob.
For simple pendulum system as per Gregory and James (2005),
T = 2 π √ ( l
g )
So,
T 2=4 π2
( l
g ) (I)
Where, T = Time taken for one oscillation for pendulum (S)
g = Acceleration due to gravity (m/s2)
l = Length of the pendulum (m)
2

From equation (I),
Square of time period of simple pendulum is directly proportional to the length
of the pendulum. So the graph of the l vs T 2 is always a simple straight line.
Procedure:-
To perform this experiment, you need one metal bob with weight, a string to connect this bob
with any fixed support as shown in the diagram above, a stopwatch to measure the time and
measure tap or scale to measure the length of the pendulum.
 Attach the metal bob with the flexible string properly.
 Fix the string with the fixed pivot point.
 Set the length of the pendulum as described in the below table.
 Give small displacement (not more than 10 degrees on either side) to the bob so it
start to oscillate.
 Measure the time period for the 10 oscillation of the bob.
 Calculate period of oscillation and acceleration due to gravity as given in the table
below.
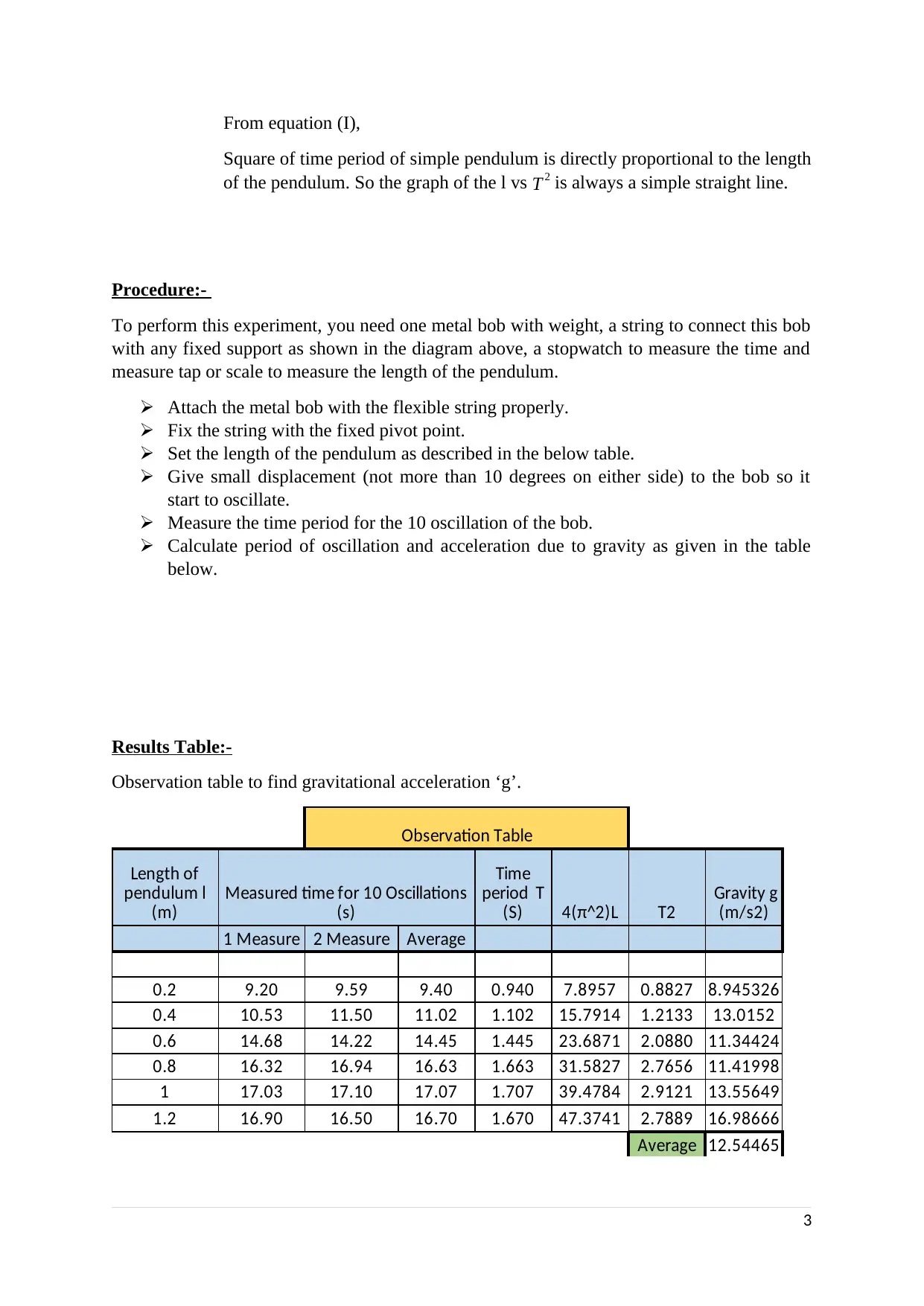
Results Table:-
Observation table to find gravitational acceleration ‘g’.
Observation Table
4(π^2)L T2
1 Measure 2 Measure Average
0.2 9.20 9.59 9.40 0.940 7.8957 0.8827 8.945326
0.4 10.53 11.50 11.02 1.102 15.7914 1.2133 13.0152
0.6 14.68 14.22 14.45 1.445 23.6871 2.0880 11.34424
0.8 16.32 16.94 16.63 1.663 31.5827 2.7656 11.41998
1 17.03 17.10 17.07 1.707 39.4784 2.9121 13.55649
1.2 16.90 16.50 16.70 1.670 47.3741 2.7889 16.98666
Average 12.54465
Length of
pendulum l
(m)
Measured time for 10 Oscillations
(s)
Time
period T
(S)
Gravity g
(m/s2)
3

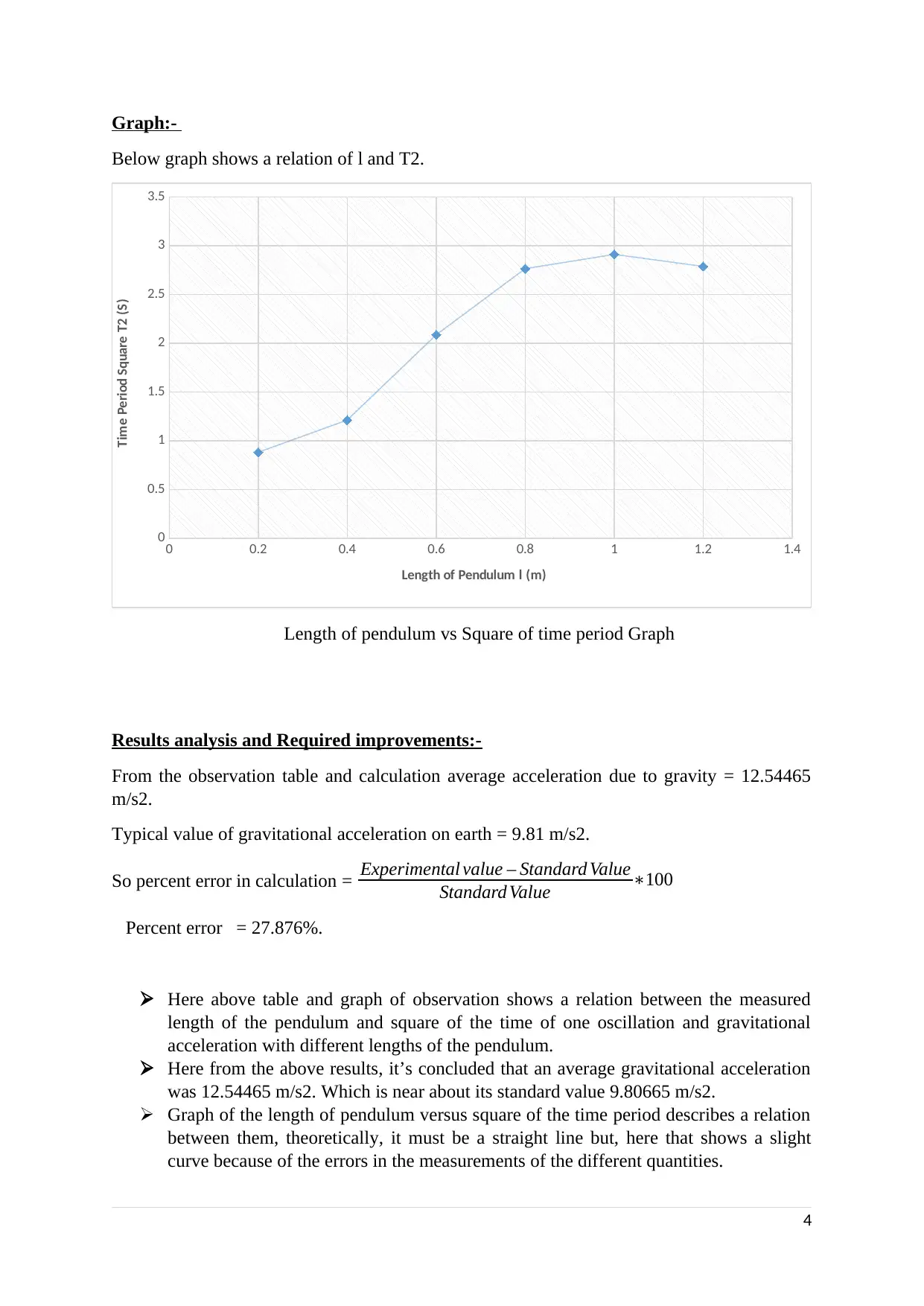
Graph:-
Below graph shows a relation of l and T2.
0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.5
1
1.5
2
2.5
3
3.5
Length of Pendulum l (m)
Time Period Square T2 (S)
Length of pendulum vs Square of time period Graph
Results analysis and Required improvements:-
From the observation table and calculation average acceleration due to gravity = 12.54465
m/s2.
Typical value of gravitational acceleration on earth = 9.81 m/s2.
So percent error in calculation = Experimental value – Standard Value
Standard Value ∗100
Percent error = 27.876%.
 Here above table and graph of observation shows a relation between the measured
length of the pendulum and square of the time of one oscillation and gravitational
acceleration with different lengths of the pendulum.
 Here from the above results, it’s concluded that an average gravitational acceleration
was 12.54465 m/s2. Which is near about its standard value 9.80665 m/s2.
 Graph of the length of pendulum versus square of the time period describes a relation
between them, theoretically, it must be a straight line but, here that shows a slight
curve because of the errors in the measurements of the different quantities.
4

 As discussed earlier, there is an assumption for use of the equation, like a string must
be weightless but in the actual condition, it also has some mass. Secondly, it’s also
assumed that string must be fully flexible but in the real world it’s impossible to find
out weightless and fully flexible string, it always has some mass and rigidity,
therefore it impacted the final results slightly.
 After that, Here assumed that string was inextensible so that it not get a contract or
expand due to weight but in the real case, it was also impossible to find the string
which not get expand or contract during oscillation.
 As described by Pirooz and Shankar (2017), the flow of air around the oscillating
pendulum generates a drag force that opposes the motion of the pendulum, eventually,
pendulum loss its mechanical energy to overcome the drag force due to airflow.
Pirooz and Shankar (2017) proved that in simple pendulum system drag on string
plays an important role in the accuracy of the pendulum results. To minimize the
effect of drag force it must be required to perform the experiment into the vacuum
chamber.
 For measurement of length, there is an always scale or measure tap are used, those all
instruments also have some limited accuracy and least count. For example, if a simple
scale was used for measurement of the length it has the least count of 1mm only and
accuracy of that is also plus or minus 1mm. To minimize these errors it must require
to use the highest precision tools like Vernier calliper or micrometer screw gauge.
 For measurement of the time stopwatch is used, usually normal stopwatch has an
accuracy of 1s, there is also a possibility of error because of that. To minimize these
errors its must be needed to use the highest accuracy stopwatch. Like currently
android or apple watch also has an accuracy of 1ms, so it’s better to use these than a
simple old fashion stopwatch.
 And at final, in all of the measurement, there is human intervention, so there is also
the highest possibility to introduction of error due to limitation of acting speed of the
human body, which is highly dependent on the person who has measured the
observation.
5

References:-
Gregory L. Baker, James a Blackburn (2005). The pendulum: A case study in physics.
N Suwanpayak et al (December 2018). A comparison of gravitational acceleration
measurement methods for undergraduate experiment. Journal of Physics: Conf.
Series 1144 (2018) 012001
Pirooz and Shankar (2017). Damping of a Simple Pendulum Due to Drag on Its String.
Journal of Applied Mathematics and Physics, 2017, 5, 122-130
http://www.scirp.org/journal/jamp
6