Intermediate Macroeconomics Assignment: Growth Models and Analysis

This assignment solution provides a detailed analysis of the Solow growth model and related macroeconomic concepts. It begins with an introduction and then addresses several questions, including the Cobb-Douglas production function, steady-state conditions, and the golden rule saving rate. The solution explores the impact of changes in saving rates, depreciation, and population growth on capital accumulation and output per worker. It also delves into the human capital accumulation model, analyzing capital intensity ratios and balanced growth paths. The assignment uses graphs and equations to illustrate key concepts and provides a reference list of relevant books and journals. The document explores the relationship between saving rates, capital intensity, and economic growth, and how these factors affect steady-state income per capita. The solution offers a comprehensive understanding of the dynamics of economic growth within the framework of the Solow model and human capital accumulation.

INTERMEDIATE
MACROECONOMIC

Table of Contents
INTRODUCTION...........................................................................................................................1
Question 1...............................................................................................................................1
Question 2:..............................................................................................................................2
Question 3: .............................................................................................................................3
Question 4: ............................................................................................................................5
Question 5: .............................................................................................................................5
Question 6:..............................................................................................................................8
Question 7: ...........................................................................................................................10
REFERENCE.................................................................................................................................12

INTRODUCTION
Question 1
Solution: Solow Growth is a key which consider as basis for modern economic growth.
According to Cobb-Douglas production functions:
Y = F (K, AN)
= Kα (AN)1−α
Where, output per effective worker : y = Y/AN and,
Consumption per effective worker : k ≡ K/AN.
Investment per worker i = 1/AN.
Therefore, Y = Kα (AN)1−α
Y/ AN = (K/ AN) α
y= k α
In this regard, Steady state in Solow model :
s f (kss) = δ kss
i.e. kss/ f (kss) = s/ δ
As per given Table:
Benchmark Parameter values
α 1/3
s 3%
δ 18%
gA 3.0%
gB 2.0%
Therefore, Cobb Douglas case, capital per worker can be estimated as:
s (kss) α = δ kss
kss = (s/ δ)1/1−α
= (0.03/0.18) 3/2
= 0.0339
Golden rule saving rate (kgr): According to Solow Model, it has predicted that countries having
rate of savings and investment, will have higher output per effective worker.
1

Therefore, level of capital worker (kgr) maximizes when
css = f(k) – δk
First order condition with respect to k,
dy/dk = δ
or, f’(kgr) = δ
or, α (kgr) α-1 = δ
or, kgr = (α/ δ) 1/1−α
here, α=1/3, δ = 18%
then, kgr = 2.516
Question 2:
Solution: As economy begins with initial steady state, therefore, economy of nation devotes a
small share to consumption. This would is said to be an immediate effect of contribution of
larger share of national output to investment. In this regard, higher investment rate shows that
capital stock increases at rapid rate. So, productivity of employees or output per effective worker
also rises.
In context with new steady state, generally output raise at rate n+g and output per
worker at rate g. Therefore, productivity seems to be independent from investment rate.
(i) Begins with steady state condition, sy = (δ+n+g)k
Or, s = (δ+n+g)k/y
Here, δ is depreciation or saving rate and equals to 0.03 (from 18% to 15%).
And, capital- output ratio (k/y)= 2.5 and growth rate of output (n+g) = 3%
Therefore, new steady state condition can be calculated as
= (0.03 + 0.03)/ 2.5 = 0.024
Thus, new steady state is 24%.
Therefore, beginning with an initial steady state, higher steady state shows high level of
consumption. Under this condition, increase in investment rate will raise productivity growth rate
also but in short run. Because for long run, it has no effect.
(ii) marginal capital per effective worker, differentiate function f with respect to K
MPK = δF/ δK
= α Kα-1(AN)1−α
= α (K/AN)α-1
2

= α kα-1
In order to get marginal output per effective worker, differentiate function F with respect to N,
MPK = δF/ δN
= A(1- α) Kα (AN)−α
= A (1- α) (K/AN)α
= A (1-α) kα-1
Using Cobb-Douglas, Y = Kα (AN)1−α
therefore, Taking log on both sides,
ln Y = α ln K + (1- α) ln A + (1- α) ln N
Question 3:
Solution: Economists generally prefer to work at highest possible level of generality to make
sure that certain assumptions will not lead to draw invalid conclusion. Due to this reason, Solow
model doesn't specify a particular functional form of production function. In general, they use
Y = F (K, AN) = Kα (AN)1−α
where, α is a parameter lies between 0 to 1. In intensive form, this function can be return as
f(k) = kα
In Australia, population grow by 2% with Net Overseas Migration, therefore, migration flow is
considered as major key factor contribute to population growth. Over the last decades, the
planned migration is increasing at constant rate. Therefore, government wants to pass a new
immigration law in order to make easy to immigrate to this country.
In this regard, small growth rates can be compounded up to high differences in levels
over long period of time. Therefore, growth rate can be represented as
xt + i = (1+gx)j Xt
since, growth rate Gn is 2% therefore,
xt + 10 / Xt = (1 + 0.02)10 = 1.22
but if Gn is increasing from 2% to 4% therefore,
xt + 10 / Xt = (1 + 0.04)10 = 1.48
Now by plotting the time-path of capital per effective worker and log output per worker for 100
years, as shown below can be defined as:-
3

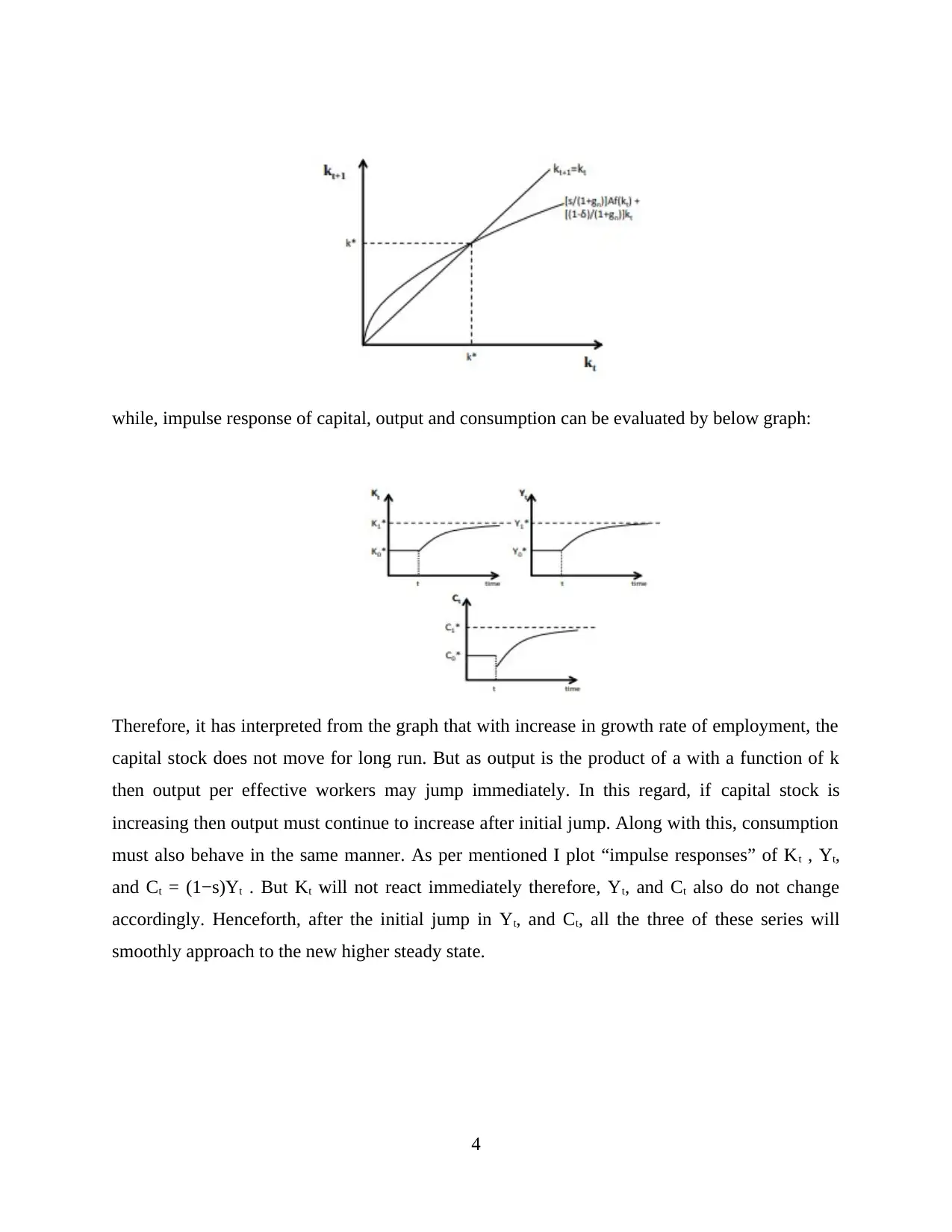
while, impulse response of capital, output and consumption can be evaluated by below graph:
Therefore, it has interpreted from the graph that with increase in growth rate of employment, the
capital stock does not move for long run. But as output is the product of a with a function of k
then output per effective workers may jump immediately. In this regard, if capital stock is
increasing then output must continue to increase after initial jump. Along with this, consumption
must also behave in the same manner. As per mentioned I plot “impulse responses” of Kt , Yt,
and Ct = (1−s)Yt . But Kt will not react immediately therefore, Yt, and Ct also do not change
accordingly. Henceforth, after the initial jump in Yt, and Ct, all the three of these series will
smoothly approach to the new higher steady state.
4

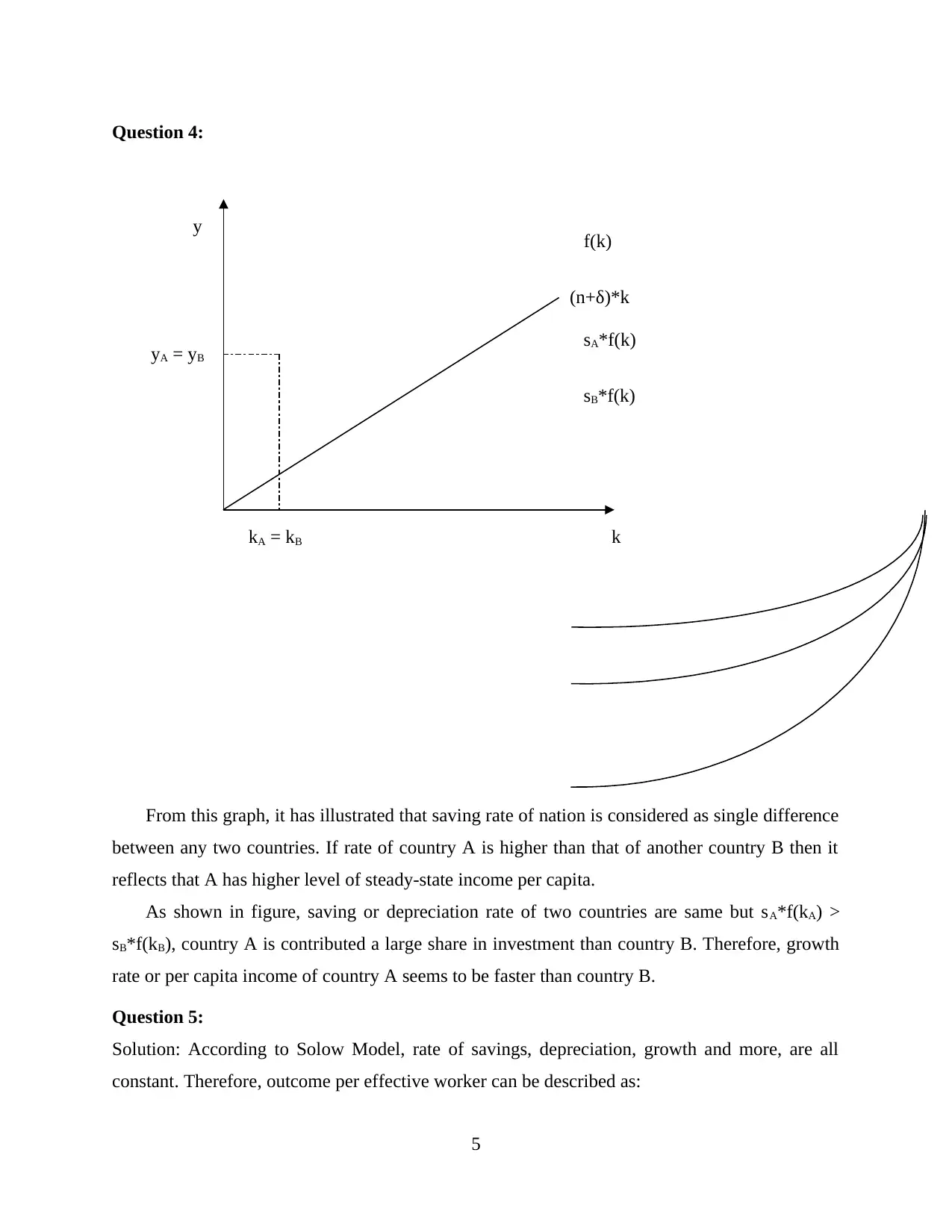
Question 4:
From this graph, it has illustrated that saving rate of nation is considered as single difference
between any two countries. If rate of country A is higher than that of another country B then it
reflects that A has higher level of steady-state income per capita.
As shown in figure, saving or depreciation rate of two countries are same but sA*f(kA) >
sB*f(kB), country A is contributed a large share in investment than country B. Therefore, growth
rate or per capita income of country A seems to be faster than country B.
Question 5:
Solution: According to Solow Model, rate of savings, depreciation, growth and more, are all
constant. Therefore, outcome per effective worker can be described as:
5
f(k)
(n+δ)*k
k
y
sA*f(k)
sB*f(k)
yA = yB
kA = kB

Y = Kα (AN)1−α
Y/ AN = (K/ AN) α
y= k α
where K is capital and AN is labor.
At α = ½,
y = k1/2
When saving rate (s) of one country is 0.08, then capital, production and consumption per
worker in the steady state can be calculated as:
k = (s/ n+ δ)2 = (0.08/ n+ δ)2
Similarly, when saving rate is 0.18 then k = (0.18/ n+ δ)2
6

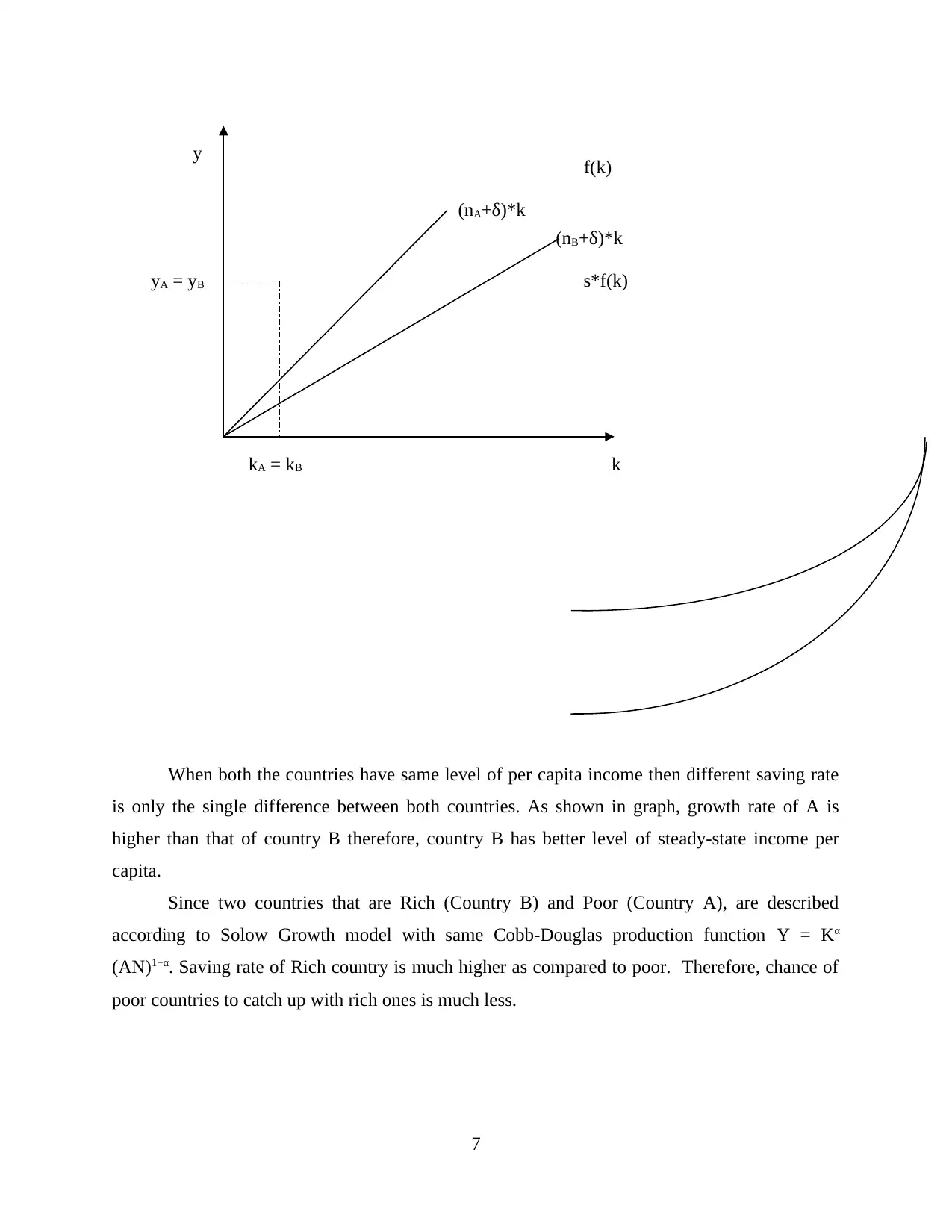
When both the countries have same level of per capita income then different saving rate
is only the single difference between both countries. As shown in graph, growth rate of A is
higher than that of country B therefore, country B has better level of steady-state income per
capita.
Since two countries that are Rich (Country B) and Poor (Country A), are described
according to Solow Growth model with same Cobb-Douglas production function Y = Kα
(AN)1−α. Saving rate of Rich country is much higher as compared to poor. Therefore, chance of
poor countries to catch up with rich ones is much less.
7
f(k)
(nB+δ)*k
k
y
s*f(k)yA = yB
kA = kB
(nA+δ)*k

Question 6:
Solution: In human capital accumulation model, capital intensity ratio in year t can be defined as
Фt = Ht / Kt . Therefore, a fraction sK of output is invested in physical capital and a fraction of sK
is invested in human capital
K t+1 − Kt = sK Yt − δK t
and
H t+1 − Ht = sH Yt − δH t
Therefore, at sH = 0.4 and sK = 0.3, α = 0.5, A =1 and δ = 0.05 then steady-state value of
capital intensity ratio Ф can be calculated as:-
K t+1 - Kt = (sK Yt ) − (δK t)
= (sK AK t) - (δK t)
= (sK A – δ) K t
or, K t+1 / Kt - 1 = (sK A – δ)
or, K t+1 / Kt = (sK A – δ) + 1
= (0.3 x 1 – 0.05) + 1
= 0.25 + 1 = 1.25
Similarly, H t+1 − Ht = (sH Yt) − (δH t)
= (sH AHt ) − (δH t)
= (sH A− δ) H t
or, Ht+1 / Ht = (sH A− δ) +1
= ( 0.4 x 1 – 0.05 ) + 1
= ( 0.35 + 1) = 1.35
8

So, steady-state value of capital intensity ratio Фt = Ht / Kt
According to balanced growth path,
Ht = Фt Kt
therefore, production function can be written
Yt = A (Kt)α (Ht) 1−α
= A (Kt)α (Фt x Kt ) 1−α
= A (Kt) (Фt ) 1−α
Hence there is no diminishing returns to K.
Along with this, balanced growth path Ht and Kt are in constant proportions
Therefore, Physical capital accumulation is now
K t+1 − K t = gt Kt
= [sK A (Kt) (Фt ) 1−α ] - [δK t]
where, g is endogenous growth rate and calculated by,
gt = sK A (Фt ) 1−α ] - δ
since Фt = sH / sK
it implies to- gt = sK A (sH / sK) 1−α ] - δ
= s A – δ where s = (sH )α x (sK) 1−α
Therefore, s = (0.4)1/2 x (0.3) ½
= 0.346
and, gt = 0.346 x 1 – 0.05
= 0.296
9

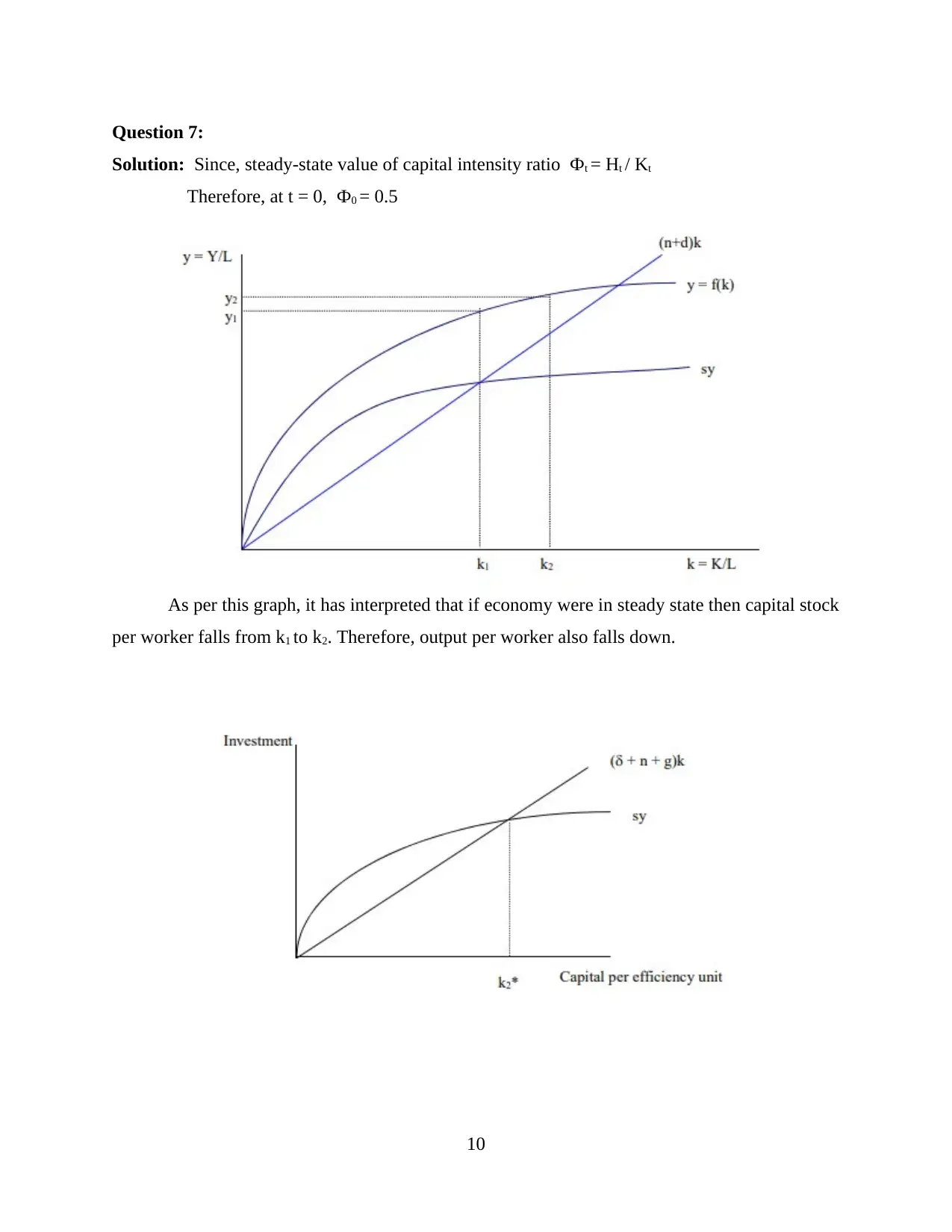
Question 7:
Solution: Since, steady-state value of capital intensity ratio Фt = Ht / Kt
Therefore, at t = 0, Ф0 = 0.5
As per this graph, it has interpreted that if economy were in steady state then capital stock
per worker falls from k1 to k2. Therefore, output per worker also falls down.
10

11

REFERENCE
Books and Journals
Poutineau, J. C. and Vermandel, G., 2015. A primer on macroprudential policy. The Journal of
Economic Education. 46(1). pp.68-82.
Kung, H., 2015. Macroeconomic linkages between monetary policy and the term structure of
interest rates. Journal of Financial Economics. 115(1). pp.42-57.
Montgomery, H.B., 2017. Energy price shocks and macroeconomic performance. Routledge.
Weale, M., and et. al., 2015. Macroeconomic policy: inflation, wealth and the exchange rate.
Routledge.
Danthine, J. P. and Donaldson, J. B., 2014. Intermediate financial theory. academic press.
Gasaymeh, A. M. M., Kreishan, L. J. and Al-Dhaimat, Y. A., 2014. The Effects of Age, Gender,
and Major on Measures of Jordanian Students’ Attitudes towards Academic Group
Learning in Computer Training Courses. Journal of Education and Practice. 5(15).
pp.173-179.
12