Mathematics Assignment: Equation Solving and Quadratic Equations

This document presents a comprehensive solution to a mathematics assignment, focusing on equation solving and algebraic manipulations. The solution addresses several key areas, including solving linear equations, quadratic equations, and problems involving parallel lines and geometric theorems. The assignment includes detailed step-by-step solutions for each problem, demonstrating the application of various mathematical concepts and techniques such as factorization, the quadratic formula, and the Pythagorean theorem. Furthermore, the document covers topics such as determining the similarity and congruence of triangles, calculating the area and circumference of circles, and expanding and factoring algebraic expressions. The solutions provide clear explanations and justifications for each step, ensuring a thorough understanding of the mathematical principles involved. This document serves as a valuable resource for students seeking to enhance their problem-solving skills and deepen their understanding of fundamental mathematical concepts.

MATHS
omsairam
[Pick the date]

Question 3
(a) 3t = (7k/13) – 17
3t + 17 = (7k/13) – 17 + 17 (By adding 17 on both sides)
3t + 17 = (7k/13)
(3t+17)(13/7) =(7k/13)(13/7) (By multiplying 13/7 on both sides)
Hence, k = (13/7) (3t+17)
(b) 7k = (4k/3t) – 11t
7k + 11t = (4k/3t) – 11t + 11t (Adding 11t on both sides)
7k + 11t = (4k/3t)
Taking 7k to the RHS, we get
11t = (4k/3t) – 7k
11t = k [(4/3t) – 7] (Taking k common on RHS)
Hence, k = 11t[(4/3t) – 7]
Thus, k = (44/3)t2 – 77t
Question 4
(a) Number of teenagers = 26
Computation of Cinema Costs
Cinema charges = 4*26 = £104
Transport charges to cinema = £90
Hence, total cinema cost = 104+ 90 = £194
Computation of bowling costs
Bowling alley charges = 5.5*26 = £143
Transport charges to bowling = £45
Hence, total bowling costs = 143 + 45 = £188

Number of teenagers = 38
Computation of Cinema Costs
Cinema charges = 4*38 = £152
Transport charges to cinema = £90
Hence, total cinema cost = 152+ 90 = £242
Computation of bowling costs
Bowling alley charges = 5.5*38= £209
Transport charges to bowling = £45
Hence, total bowling costs = 209 + 45 = £254
(b) For the cinema charges, the relevant equation is given as y = 4x + 90
The above equation holds since £90 is a fixed transportation cost for the group and is
independent of the number of teenagers. Further, the cost of cinema per teenager is £4 and
hence, the variable cost would be 4x where x is the number of teenagers.
With regards to bowling, fixed transport charges are £45. Also, per teenager cost for bowling
alley is £5.5.
Hence, y = 5.5x + 45
(c ) (i) The relevant costs are captured in the table below.
The relevant graph is indicated below.

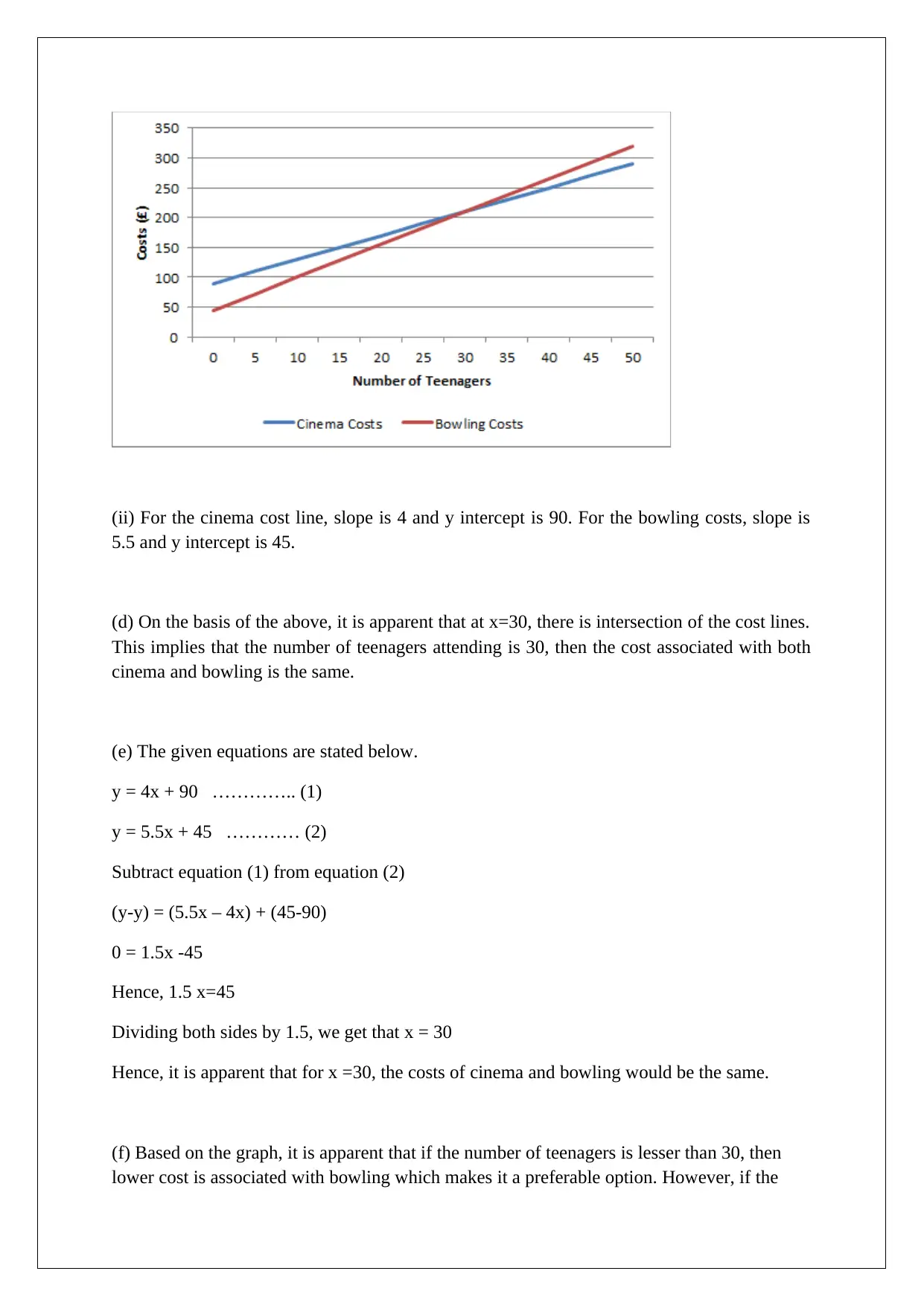
(ii) For the cinema cost line, slope is 4 and y intercept is 90. For the bowling costs, slope is
5.5 and y intercept is 45.
(d) On the basis of the above, it is apparent that at x=30, there is intersection of the cost lines.
This implies that the number of teenagers attending is 30, then the cost associated with both
cinema and bowling is the same.
(e) The given equations are stated below.
y = 4x + 90 ………….. (1)
y = 5.5x + 45 ………… (2)
Subtract equation (1) from equation (2)
(y-y) = (5.5x – 4x) + (45-90)
0 = 1.5x -45
Hence, 1.5 x=45
Dividing both sides by 1.5, we get that x = 30
Hence, it is apparent that for x =30, the costs of cinema and bowling would be the same.
(f) Based on the graph, it is apparent that if the number of teenagers is lesser than 30, then
lower cost is associated with bowling which makes it a preferable option. However, if the

teenager count exceeds 30, then cinema costs become lower than bowling costs and hence the
preferred option changes. Further, for 30 teenagers, the cost associated with both cinema and
bowling is the same and thus, any option may be chosen.
Question 5
(a) (i) It is known that straight lines BCG and EF are parallel.
As a result, ∠BCA = ∠EFD owing to these angles being corresponding angles.
Also, ∠EFD is given as 650
Hence, ∠BCA = 650
(ii) It is known that straight lines GDE and AB are parallel.
As a result, ∠BAC = ∠EDF owing to these angles being corresponding angles.
Also, from (i), it is known that ∠BCA = ∠EFD
Hence, in ∆ ABC and ∆ DEF, if two angles are equal, then the third corresponding angles
would also be equal since for all triangles, the sum of interior angles is 1800.
Therefore, ∠DEF = ∠ABC = 550
(iii) Based on the results obtained above in (i) and (ii), it is apparent that
∠BAC = ∠EDF
∠ABC = ∠DEF
∠BCA = ∠EFD
Owing to the three corresponding angles of the two triangles being equal to each other, hence
by AAA (angle-angle-angle) similarity theorem, it can be concluded that ∆ ABC and ∆ DEF
are similar.
(b) As per angle sum property, the sum of interior angles of a triangle is 1800.
Hence, for ∆AEB, ∠AEB = 180 – (35+38) = 1070
Also, for ∆CDB, ∠DBC = 180 – (107+38) = 350
Now, looking at ∆ABE and ∆BCD
∠AEB = ∠CDB
Also, EA = DB

Further, ∠EAB = ∠DBC
Hence, by SAS (Side-Angle-Side), it can be concluded that ∆ABE and ∆BCD are congruent.
(c) (i) It is known that AB = 50 cm
Also, since E is the midpoint hence, EB = 50/2 = 25 cm
In triangle EDB, in accordance with Pythagoras Theorem
ED2 + EB2 = BD2
ED2 + 252 = 352
Hence, ED2 = 352 – 252 = 1225-625 = 600
Thus, ED = 24.49 cm (approximately)
(ii) Since D is the center of the circle, hence DB and CD are both radii of the circle. As a
result DB = CD = 35 cm.
Hence, EC = ED + DC = 24.49 + 35 = 59.49 cm
(iii) Area of triangle EBC = (1/2)*(EB) (EC) = (1/2) (25)(59) = 743.63 cm2
(iv) It is known that radius of the given circle is 35 cm
Hence, area of circle = πr2 = (22/7)*(352) = 3850 cm2
Circumference of circle = 2πr = 2*(22/7)*35 = 220 cm
(v) It is known that radius of the given circle is 35 cm
Hence, area of circle = πr2 = (22/7)*(352) = 3850 cm2
Circumference of circle = 2πr = 2*(22/7)*35 = 220 cm
Question 6
a) i) (9x-13)(11x+5)

= (9x*11x) + (9x*5) + (-13*11x) + (-13*5)
= 99x2 + 45x – 143x – 65
= 99x2 – 98x – 65
ii) (7a-4b)2
The following identity would be applicable here.
(x-y)2 = x2 + y2 – 2xy
Hence, (7a-4b)2 = (7a)2 + (4b)2 – 2*(7a)(4b)
= 49a2 + 16b2 -56ab
b) i) x2-22x-48
= x2 -24x + 2x – 48
= x(x-24) + 2(x-24)
= (x+2) (x-24)
ii) 25h2 – 64k2
= (5h)2 – (8k)2
The following identity can be used here.
x2 – y2 = (x+y)(x-y)
= (5h+8k)(5h-8k)
c) (i) x2 + 11x -42 = 0
The given quadratic equation can be factorized using middle term split.
Hence, the above quadratic equation can be written as follows.
= x2 + 14x – 3x – 42
=x(x+14) -3(x+14)
=(x-3)(x+14)
Hence, x2 + 11x -42 = (x-3)(x+14)
Thus, either (x-3) = 0 or (x+14) = 0

As a result, x is either 3 or -14.
Check:
(x-3) (x+14) = 0
Putting x =3, the LHS = (3-3) (3+14) = 0
Clearly, the LHS = RHS and hence x=3 is a solution
Similarly, putting x=-14, LHS = (-14-3)(-14+14) = 0
Clearly, the LHS = RHS and hence x=-14 is a solution
ii) 4x2 + 44x -168
Taking 4 as common, we get
= 4(x2 + 11x-42)
However from part c(i), it is apparent that
x2 + 11x-42 = (x-3)(x+14)
Hence, the given equation can be factorized as 4(x-3)(x+14)
Thus, 4(x-3)(x+14) = 0
The above implies that either (x-3) = 0 or (x+14) = 0
Hence, x=3 or x=-14
Check:
4(x-3) (x+14) = 0
Putting x =3, the LHS = 4(3-3) (3+14) = 0
Clearly, the LHS = RHS and hence x=3 is a solution
Similarly, putting x=-14, LHS = 4(-14-3)(-14+14) = 0
Clearly, the LHS = RHS and hence x=-14 is a solution
iii) 11/(x-3) = 7/(x-7)
Multiplying the above equation with (x-3)(x-7) on both sides, we get
11(x-7) = 7(x-3)

11x – 77 = 7x -21
Adding -7x + 21 on both sides, we get
11x – 77 -7x + 21 = 0
4x – 56 = 0
4x = 56 (By adding 56 on both sides)
Hence, x = (56/4) = 14
Check:
LHS = 11/(x-3) = 11/(14-3) = 1
RHS = 7/(x-7) = 7/(14-7) = 1
Since, LHS = RHS, hence the computed solution is correct
Question 7
a) The given equation is as follows.
x2 – 19x = 0
Substituting x=19 in the above equation, we get
Left Hand Side (LHS) = (19)2 – 19*19 = 0
Also, Right Hand Side (RHS) = 0
Since, LHS = RHS, hence we can conclude that x=19 is a solution to the given equation since
it satisfies the given equation.
b) x2 – 19x = 0
Taking x out as common, we get
x(x-19) = 0
It implies that either x = 0 or (x-19) = 0
As a result, x is either 0 or 19
Hence, the two solutions of the given equation are x=0, 19
c) The solution of the student is incomplete as the only solution obtained in the working is
x=19 while the other solution x=0 is missed out. It is noteworthy that the highest power of
the equation is 2 which implies that there would be 2 solutions or roots. Also, dividing
both sides by x is permissible only under the assumption that x ≠ 0 which is not true here.