MAE256 T1 Assignment: Regression Analysis of University Data - T1

This assignment presents a detailed statistical analysis of university data, focusing on the factors influencing Vice-Chancellor remuneration. It begins with descriptive statistics of variables such as remuneration, rank, and student numbers, highlighting measures of central tendency and dispersion. The analysis then progresses to simple and multiple regression models, exploring the relationships between remuneration and university rank, and student numbers. Log-log specifications are used to assess the elasticity of remuneration with respect to rank and student numbers. Hypothesis testing is conducted to determine the significance of regression coefficients, including the impact of variables like 'grademp' and 'gradstudy'. The assignment also evaluates the overall significance of the models and the effect of university location on remuneration. The analysis includes R-squared values to compare the goodness of fit of different models. The document concludes with a discussion of the findings and relevant references.

MAE256 T1
Assignment
Student Name
[Pick the date]

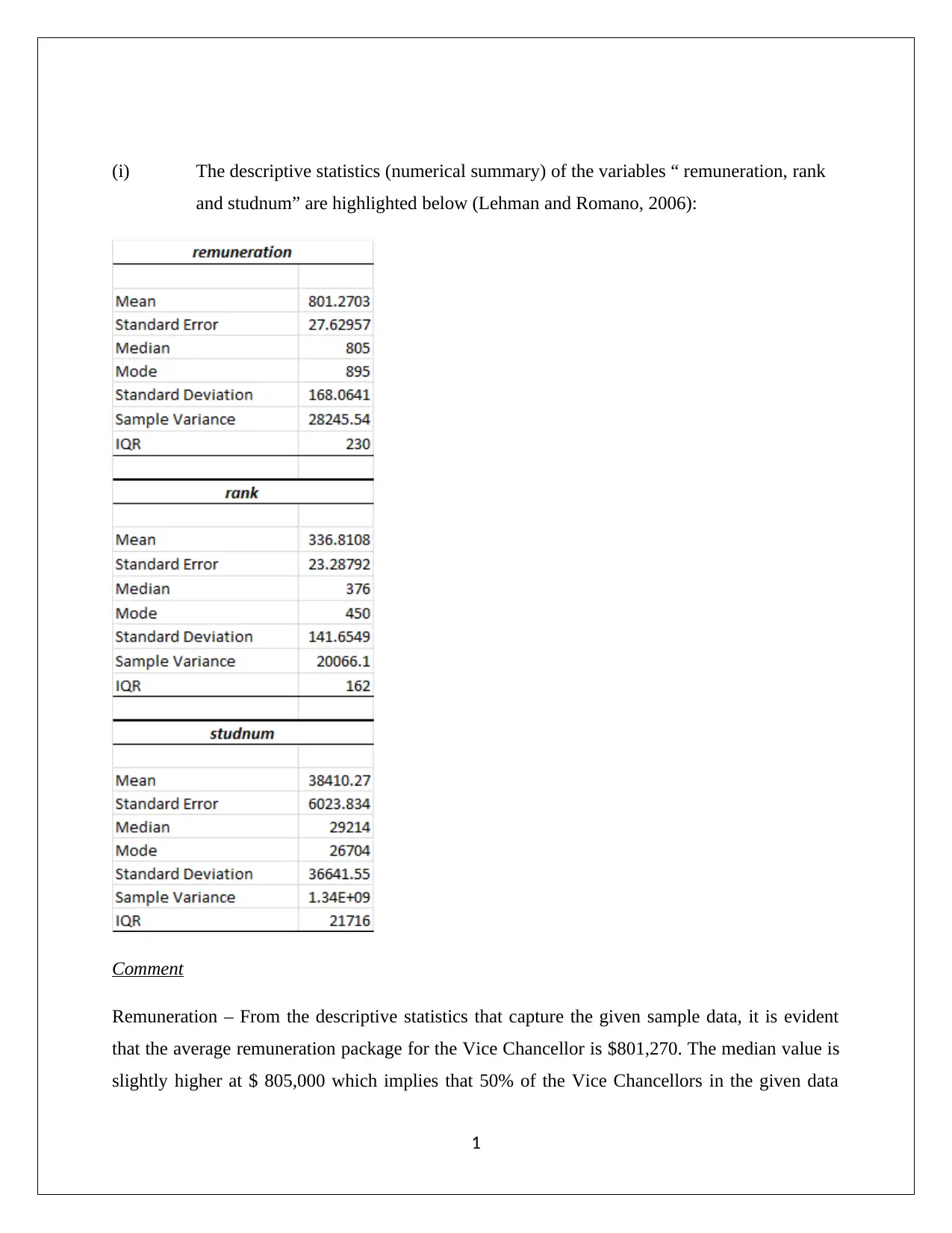
(i) The descriptive statistics (numerical summary) of the variables “ remuneration, rank
and studnum” are highlighted below (Lehman and Romano, 2006):
Comment
Remuneration – From the descriptive statistics that capture the given sample data, it is evident
that the average remuneration package for the Vice Chancellor is $801,270. The median value is
slightly higher at $ 805,000 which implies that 50% of the Vice Chancellors in the given data
1

would have salary equal to or lower than $ 805,000. However, the mode value is still higher at $
895,000. The non-coincidence of the central tendency measures is an indication that the
probability distribution in the given case would not be normal. Also, there would be presence of
negative skew having a slight distortionary effect on the average value. The standard deviation
for the salaries is low to medium indicating that while disparities do exist they do not tend to be
too extreme. The IQR values highlights that 50% of the values i.e. from 25% to 75% would lie
within this compensation interval of about $230,000 (Fehr and Grossman, 2003).
Rank – The average rank of the University in the given sample is 336.81. The median rank is
however significantly greater at 376 which implies that 50% of the sample universities have a
rank lower than or equal to 376. The deviation between the median and mode values is indicative
of the presence of some universities which have a considerably low rank which is responsible for
distortion of the mean. The various measures of dispersion highlight that the dispersion in rank
of the universities in the given sample is quite high considering that there are universities at both
the lower end as well as the higher end (Liberman, et. al., 2013).
Studnum – The average students studying in a university are about 38,410. The average figure is
clearly distorted owing to presence of universities with very high intake of students owing to
which the median value is comparatively much smaller at 29,214. Hence, the median is a better
indicator of the average number of students in a university rather than the mean. Further, the
measures of dispersion suggest that there is very high amount of dispersion that is seen in the
given variable for the sample data provided (Harmon, 2011).
(ii) Simple regression model
Remuneration = dependent variable
Rank = Independent variable
2

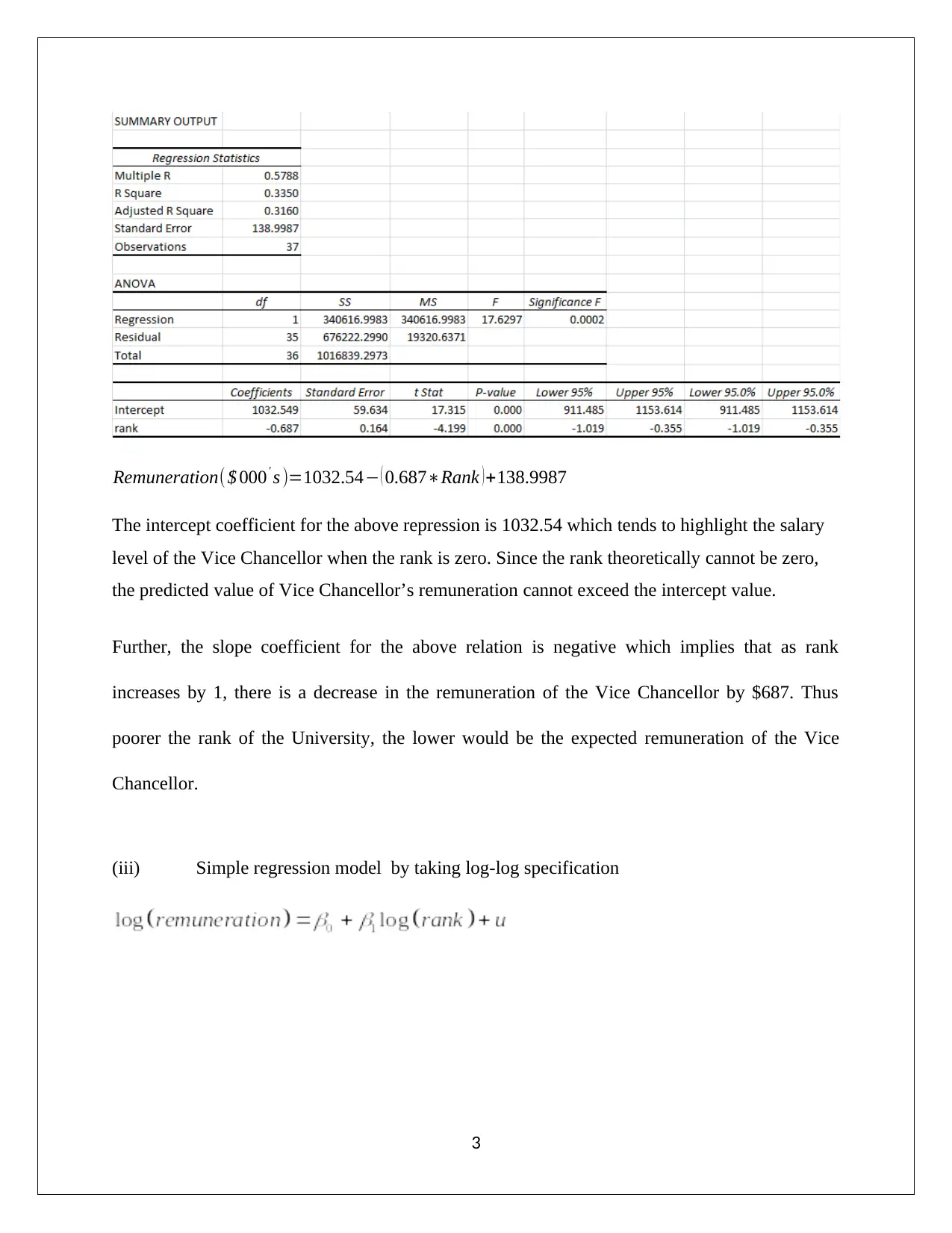
Remuneration($ 000' s )=1032.54− ( 0.687∗Rank )+138.9987
The intercept coefficient for the above repression is 1032.54 which tends to highlight the salary
level of the Vice Chancellor when the rank is zero. Since the rank theoretically cannot be zero,
the predicted value of Vice Chancellor’s remuneration cannot exceed the intercept value.
Further, the slope coefficient for the above relation is negative which implies that as rank
increases by 1, there is a decrease in the remuneration of the Vice Chancellor by $687. Thus
poorer the rank of the University, the lower would be the expected remuneration of the Vice
Chancellor.
(iii) Simple regression model by taking log-log specification
3

log ( Remuneration )=3.299−¿
The estimated coefficient of the log (rank) is -0.165. The sign of the coefficient is on expected
lines since it would be expected that Universities which are higher on the rankings would have
the Vice Chancellors drawing higher remuneration. The above model tends to validate this
logical conclusion since there is a drop in the predicted remuneration as the rank of the
University tends to increase in magnitude (Liberman, et.al., 2013).
(iv) Regression model in relation to the remuneration of university ranking based on the
number of students are highlighted below (Fehr and Grossman, 2003):
Remuneration = dependent variable
Rank, studnum = Independent variable
4

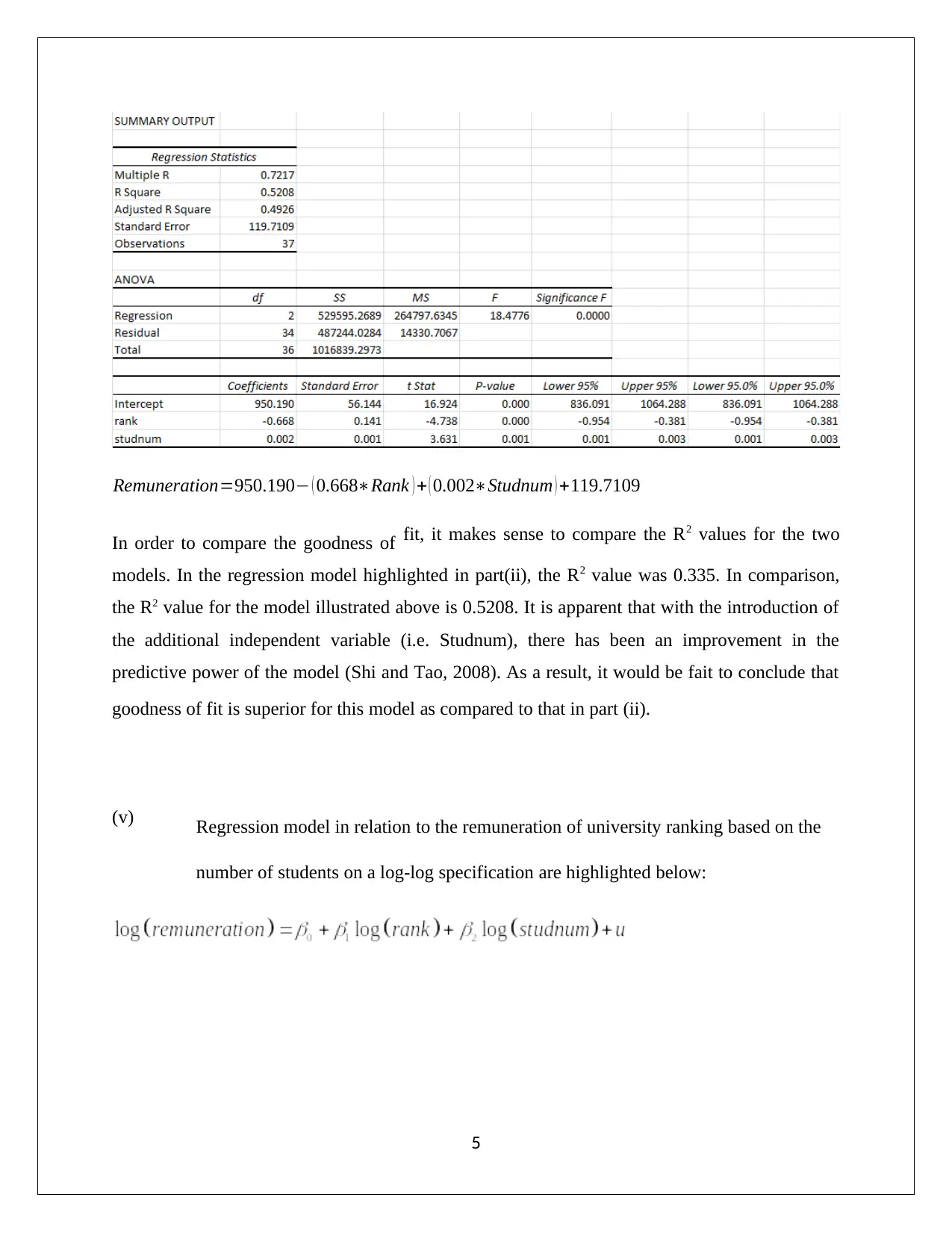
Remuneration=950.190− ( 0.668∗Rank ) + ( 0.002∗Studnum ) +119.7109
In order to compare the goodness of fit, it makes sense to compare the R2 values for the two
models. In the regression model highlighted in part(ii), the R2 value was 0.335. In comparison,
the R2 value for the model illustrated above is 0.5208. It is apparent that with the introduction of
the additional independent variable (i.e. Studnum), there has been an improvement in the
predictive power of the model (Shi and Tao, 2008). As a result, it would be fait to conclude that
goodness of fit is superior for this model as compared to that in part (ii).
(v) Regression model in relation to the remuneration of university ranking based on the
number of students on a log-log specification are highlighted below:
5

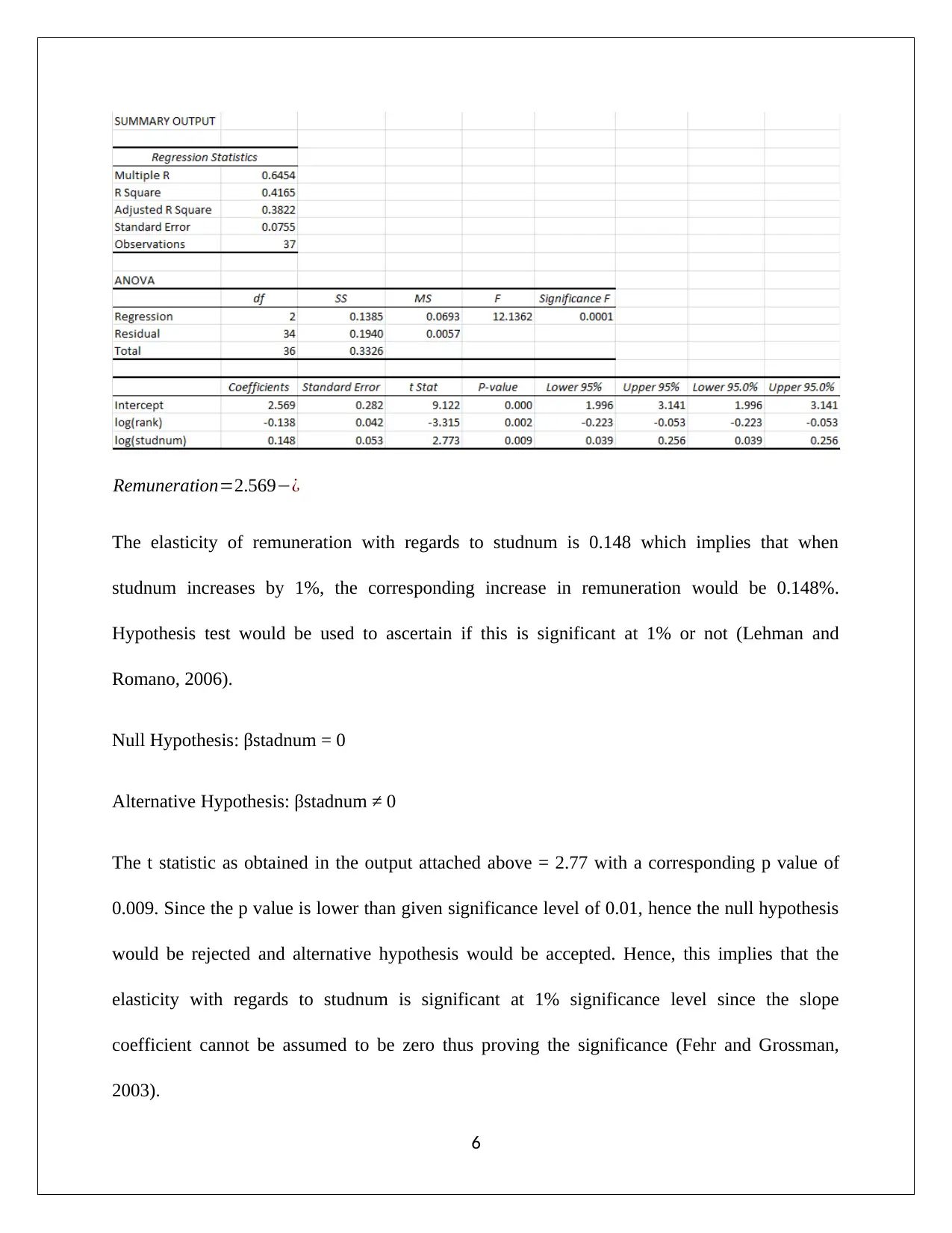
Remuneration=2.569−¿
The elasticity of remuneration with regards to studnum is 0.148 which implies that when
studnum increases by 1%, the corresponding increase in remuneration would be 0.148%.
Hypothesis test would be used to ascertain if this is significant at 1% or not (Lehman and
Romano, 2006).
Null Hypothesis: βstadnum = 0
Alternative Hypothesis: βstadnum ≠ 0
The t statistic as obtained in the output attached above = 2.77 with a corresponding p value of
0.009. Since the p value is lower than given significance level of 0.01, hence the null hypothesis
would be rejected and alternative hypothesis would be accepted. Hence, this implies that the
elasticity with regards to studnum is significant at 1% significance level since the slope
coefficient cannot be assumed to be zero thus proving the significance (Fehr and Grossman,
2003).
6

(vi) Hypothesis test would be used to ascertain if the rank slope coefficient is significant
at 1% or not.
Null Hypothesis: βRank = 0
Alternative Hypothesis: βRank ≠ 0
The t statistic as obtained in the output attached above = -3.315 with a corresponding p value of
0.002 Since the p value is lower than given significance level of 0.01, hence the null hypothesis
would be rejected and alternative hypothesis would be accepted. Hence, this implies that the
elasticity with regards to rank is significant at 1% significance level since the slope coefficient
cannot be assumed to be zero thus proving the significance (Shi and Tao, 2008). Further, this
implies that negative effect is indeed significant.
(vii) Regression model in relation to the remuneration of university ranking based on the
number of students including grademp and gradstudy on a log-log specification are
highlighted below (Fick, 2015):
7

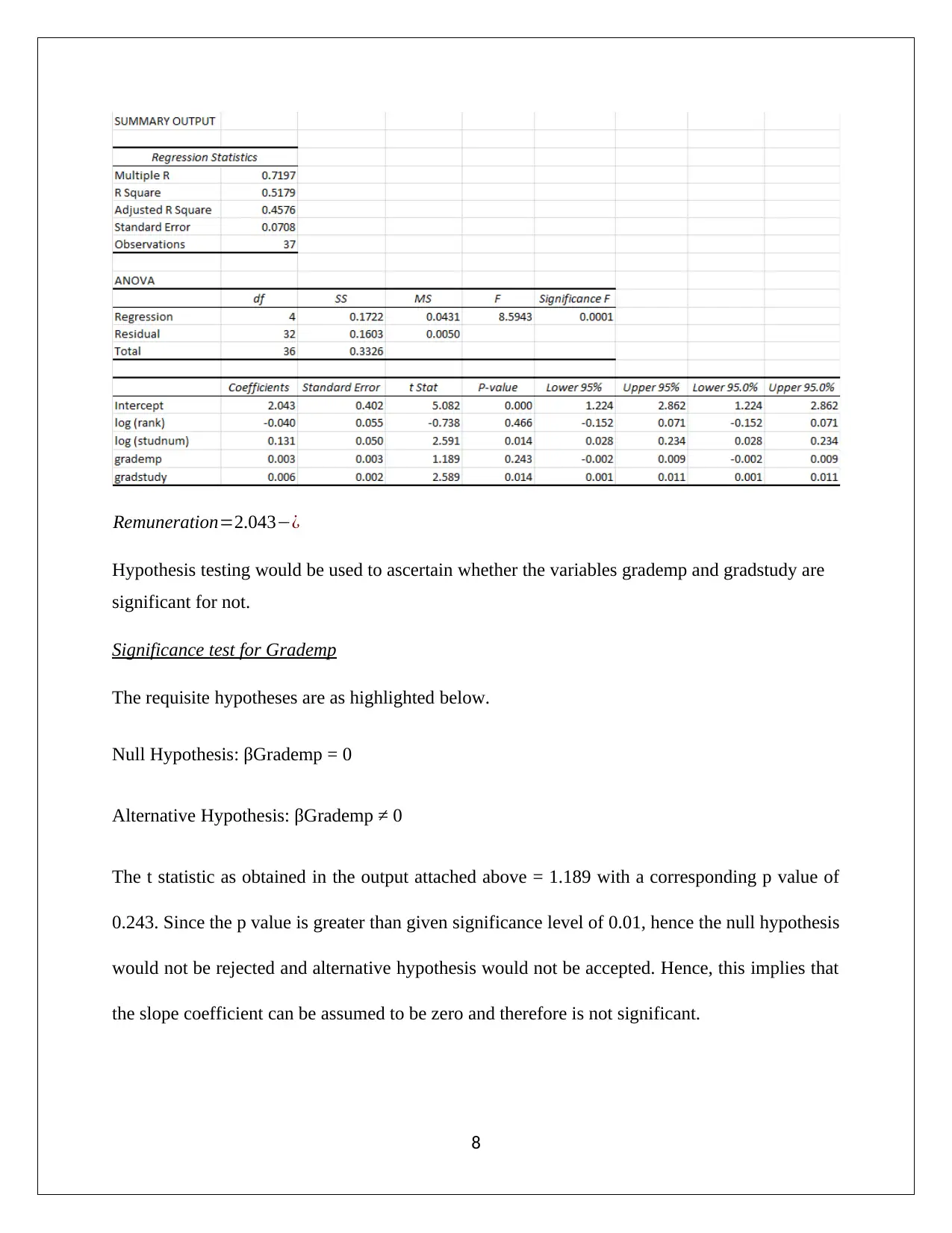
Remuneration=2.043−¿
Hypothesis testing would be used to ascertain whether the variables grademp and gradstudy are
significant for not.
Significance test for Grademp
The requisite hypotheses are as highlighted below.
Null Hypothesis: βGrademp = 0
Alternative Hypothesis: βGrademp ≠ 0
The t statistic as obtained in the output attached above = 1.189 with a corresponding p value of
0.243. Since the p value is greater than given significance level of 0.01, hence the null hypothesis
would not be rejected and alternative hypothesis would not be accepted. Hence, this implies that
the slope coefficient can be assumed to be zero and therefore is not significant.
8

Significance test for Gradstudy
The requisite hypotheses are as highlighted below.
Null Hypothesis: βGradstudy = 0
Alternative Hypothesis: βGradstudy ≠ 0
The t statistic as obtained in the output attached above = 2.589 with a corresponding p value of
0.014. Since the p value is greater than given significance level of 0.01, hence the null hypothesis
would not be rejected and alternative hypothesis would not be accepted (Eriksson and
Kovalainen, 2015). Hence, this implies that the slope coefficient can be assumed to be zero and
therefore is not significant.
Also, at 5% significance level, the joint significance of the two variables is not established since
the corresponding p value would tend to exceed 0.05.
(viii) Hypothesis test would be used to ascertain the significance of the model indicated in
part (vii).
The relevant hypotheses are highlighted below.
Null Hypothesis: All the slope coefficients are insignificant and hence can be assumed as zero.
Alternative Hypothesis: Atleast one of the slope coefficients is significant and hence cannot be
assumed to be zero.
The relevant output to perform this test is the ANOVA output as highlighted below.
9

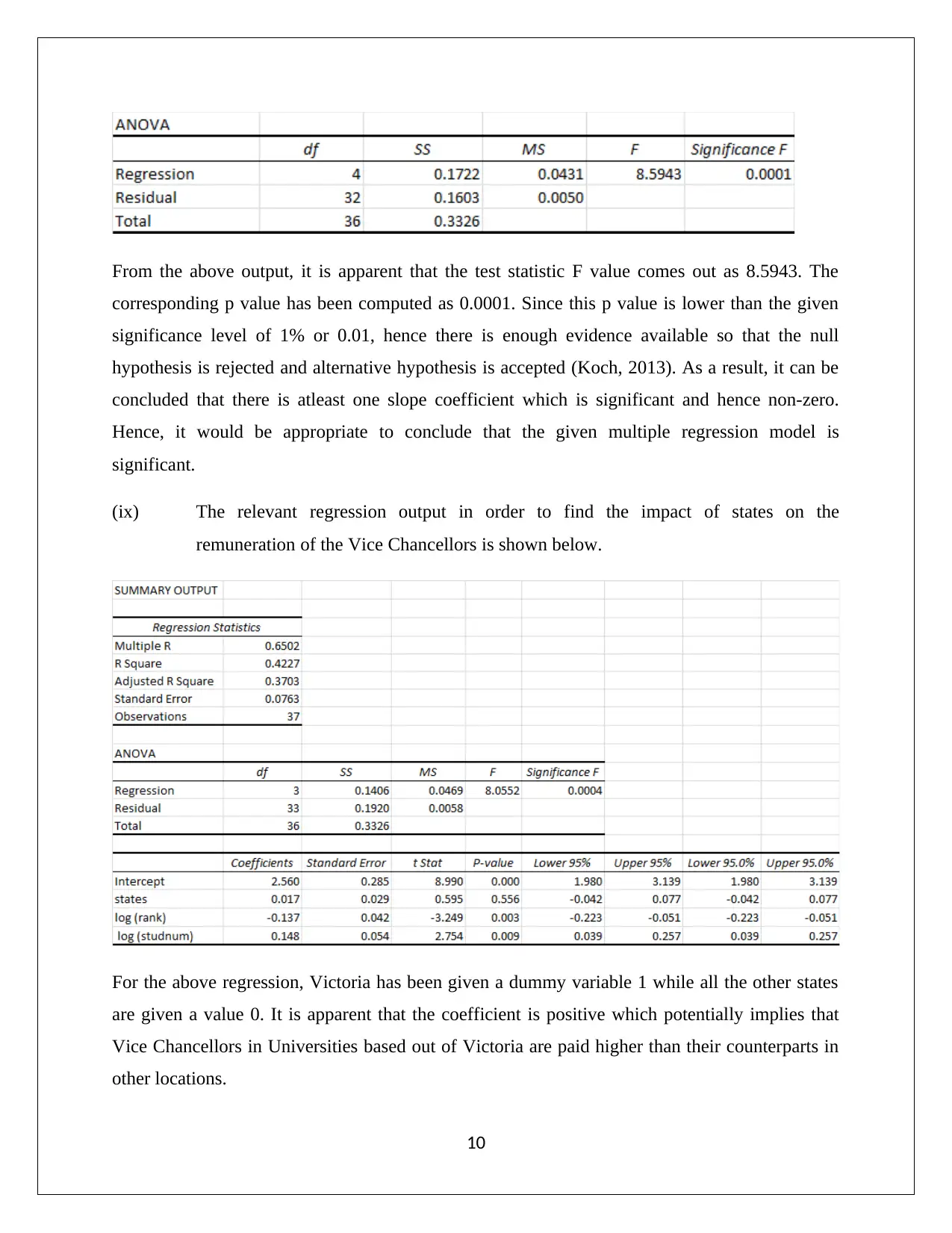
From the above output, it is apparent that the test statistic F value comes out as 8.5943. The
corresponding p value has been computed as 0.0001. Since this p value is lower than the given
significance level of 1% or 0.01, hence there is enough evidence available so that the null
hypothesis is rejected and alternative hypothesis is accepted (Koch, 2013). As a result, it can be
concluded that there is atleast one slope coefficient which is significant and hence non-zero.
Hence, it would be appropriate to conclude that the given multiple regression model is
significant.
(ix) The relevant regression output in order to find the impact of states on the
remuneration of the Vice Chancellors is shown below.
For the above regression, Victoria has been given a dummy variable 1 while all the other states
are given a value 0. It is apparent that the coefficient is positive which potentially implies that
Vice Chancellors in Universities based out of Victoria are paid higher than their counterparts in
other locations.
10

To check the significance, the following hypothesis would be taken.
Null Hypothesis: βState = 0
Alternative Hypothesis: βstate ≠ 0
The t statistic as obtained in the output attached above = 0.595 with a corresponding p value of
0.556. Since the p value is greater than given significance level of 0.05, hence the null hypothesis
would not be rejected and alternative hypothesis would not be accepted (Taylor and Taylor,
2004). Hence, this implies that the slope coefficient can be assumed to be zero and therefore is
not significant. Therefore, there is no significant effect of the location of the university on the
remuneration.
References
Eriksson, P. and Kovalainen, A. (2015) Quantitative methods in business research. 3rd edn.
London: Sage Publications.
Fehr, F. H. and Grossman, G. (2003). An introduction to sets, probability and hypothesis testing.
3rd edn. Ohio: Heath.
Flick, U. (2015) Introducing research methodology: A beginner's guide to doing a research
project. 4th edn. New York: Sage Publications.
Harmon, M. (2011) Hypothesis Testing in Excel - The Excel Statistical Master. 7th edn. Florida:
Mark Harmon.
11