Analysis of Breast Cancer Incidence Rates: Math 186 Project

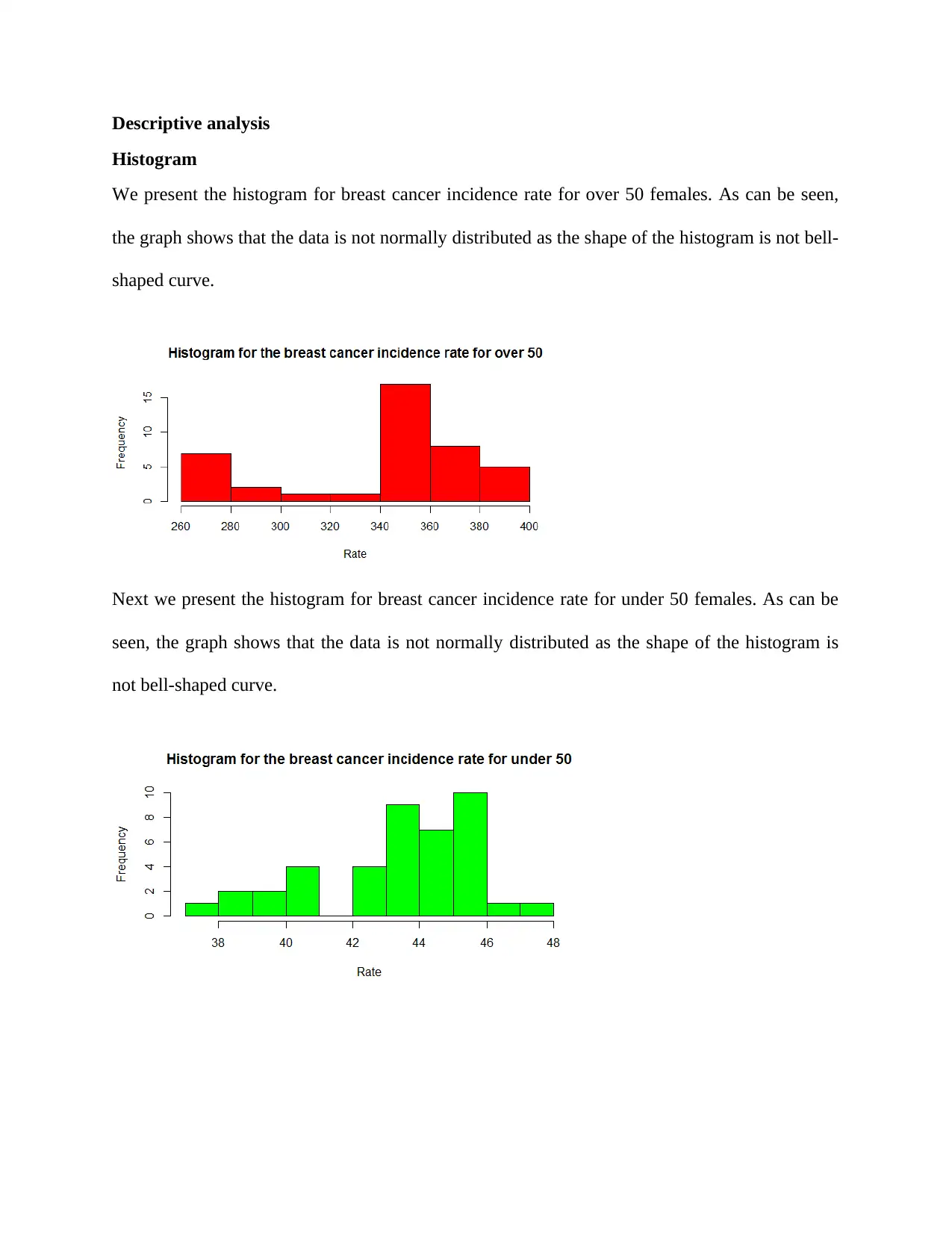
This project presents a statistical analysis of breast cancer incidence rates for females over and under 50 years old. The analysis begins with descriptive statistics, including histograms to visualize the data distribution and 5-point summaries to understand central tendency and spread. The project then investigates whether there is a significant difference between the actual and modeled breast cancer incidence rates for both age groups using t-tests. The null and alternative hypotheses are clearly defined, and the results of the t-tests, including p-values, are presented and interpreted at a 5% significance level. The project concludes by failing to reject the null hypotheses for both age groups, indicating no significant difference between the actual and modeled rates. The R code used for the analysis, including data import, histogram generation, summary statistics, and t-tests, is provided in the appendix. The project follows the guidelines of a Math 186 final project, emphasizing data organization, statistical terminology, and hypothesis testing.

Applied Mathematics
Student Name:
Instructor Name:
Course Number:
7 April 2019

Descriptive analysis
Histogram
We present the histogram for breast cancer incidence rate for over 50 females. As can be seen,
the graph shows that the data is not normally distributed as the shape of the histogram is not bell-
shaped curve.
Next we present the histogram for breast cancer incidence rate for under 50 females. As can be
seen, the graph shows that the data is not normally distributed as the shape of the histogram is
not bell-shaped curve.

5-point analysis
The table below gives the 5-point analysis for the breast cancer incidence rate for the over 50. As
can be seen, the average rate is 339.5 with the median rate being 352.9 while the maximum and
minimum rates being 397.2 and 262.3 respectively.
Is there significant difference in the actual rate and modelled rate for over 50?
We sought to test whether there exists any significant difference in the actual rate and modelled
rate. The following hypothesis was tested.
Null hypothesis (H0): There is no significant difference in the actual rate and the modelled rate
for the breast cancer incidence for female over 50.
Alternative hypothesis (HA): There is significant difference in the actual rate and the modelled
rate for the breast cancer incidence for female over 50.
A t-test was performed to test the hypothesis at 5% level of significance. The results are
presented below;
>
t.test(Rate,Modeled.Rate)
Welch Two
Sample t-test
data: Rate and
Modeled.Rate
t = -0.0051, df = 79.993,
p-value = 0.9959
alternative hypothesis:
true difference in means
is not equal to 0
95 percent confidence
interval:
-17.22356 17.13538
sample estimates:
mean of x mean of y
> summary(Rate)
Min. 1st Qu. Median
Mean 3rd Qu. Max.
262.3 333.5 352.9
339.5 362.9 397.2

As can be seen from the above, the p-value is given as 0.9959 (a value greater than 5% level of
significance), we therefore fail to reject the null hypothesis and conclude that there is no
significant difference in the actual rate and the modelled rate for the breast cancer incidence for
female over 50.
Is there significant difference in the actual rate and modelled rate for under 50?
We sought to test whether there exists any significant difference in the actual rate and modelled
rate. The following hypothesis was tested.
Null hypothesis (H0): There is no significant difference in the actual rate and the modelled rate
for the breast cancer incidence for female under 50.
Alternative hypothesis (HA): There is significant difference in the actual rate and the modelled
rate for the breast cancer incidence for female under 50.
A t-test was performed to test the hypothesis at 5% level of significance. The results are
presented below;
As can be seen from the above, the p-value is given as 0.9908 (a
value greater than 5% level of significance), we therefore fail to
reject the null hypothesis and conclude that there is no
>
t.test(Rate,Modeled.Rate)
Welch Two
Sample t-test
data: Rate and
Modeled.Rate
t = -0.0115, df = 79.676,
p-value = 0.9908
alternative hypothesis:
true difference in means
is not equal to 0
95 percent confidence
interval:
-1.030312 1.018448
sample estimates:
mean of x mean of y
43.30353 43.30947

significant difference in the actual rate and the modelled rate for the breast cancer incidence for
female under 50.
Appendix
R codes
over50<-read.csv("C:\\Users\\310187796\\Desktop\\breastcancerover50female.csv")
str(over50)
attach(over50)
par(mfrow=c(1,2))
hist(Rate, main="Histogram for the breast cancer incidence rate for over 50", col="red",
data=over50)
summary(Rate, data=over50)
t.test(Rate,Modeled.Rate, data=over50)
under50<-read.csv("C:\\Users\\310187796\\Desktop\\breastcancerunder50female.csv")
str(under50)
attach(under50)
hist(Rate, main="Histogram for the breast cancer incidence rate for under 50", col="green",
data=under50)
summary(Rate, data=under50)
t.test(Rate,Modeled.Rate, data=under50)