STA1010 Statistical Methods for Science Assignment 2 Semester 2, 2018

This assignment solution covers several statistical concepts, including binomial and Poisson distributions, normal distribution, hypothesis testing, and confidence intervals. It calculates probabilities related to drug side effects, analyzes egg weight distribution, and examines speed measurements using the Beaufort scale. Additionally, it assesses the impact of dental visits on systolic blood pressure through confidence intervals and hypothesis testing. Finally, the assignment investigates potential differences in scores between groups with and without sleep, employing pooled standard deviation and t-tests to draw conclusions about the null hypothesis. Desklib offers a wide array of study resources, including solved assignments and past papers, to support students in their academic endeavors.

Statistical Methods for Science
Assignment 2
STUDENT NAME/ID
[Pick the date]

Question 1
(a) Probability that drug cause side effect to patient p =3/100 = 0.03
Total patient n = 5
Here, the distribution would be binomial distribution.
X ( 5 , 0.03 )
¿
P ( X=x ) =(5
x )(0.03x) ¿ where , X=0 ,1 , 2 ,3 … … .. 5
(b) Probability that none of the five patients experience side effects
Here, x=0
P ( X=0 ) = ( 5
0 ) (0.030 ) ¿
Now,
Probability that at least two patients experience side effects
Here, x ≥ 2
P ( X ≥2 ) =1−P ( x< 2 )
¿ 1− ( P ( x=0 )+ P ( x=1 ) )
¿ 1−{(5
0)( 0.030) ¿
¿ 1− ( 0.8585+ 0.1328 )
¿ 0.0085
(c) Total patient n = 5

Here, the distribution would be Poisson distribution.
ƛ =np = 5(0.03) = 0.15
X ( 5 , 0.03 )
¿
P ( X=x ) =e−0.15 ( 0.15)x
x !
where , X=0 ,1 , 2 ,3 … … . .
(c) Probability that none of the five patients experience side effects
Here, x=0
P ( X=0 )= e−0.15 (0.15)0
0 ! =0.8607
Now,
Probability that at least two patients experience side effects
Here, x ≥ 2
P ( X ≥2 ) =1−P ( x< 2 )
¿ 1− ( P ( x=0 )+ P ( x=1 ) )
¿ 1− { e−0.15 ( 0.15 )0
0! + e−0.15 ( 0.15 )1
1! }
¿ 1− ( 0.8607+0.1291 )
¿ 0.0102
(d) It can be said that probabilities computed with the help of binomial distribution is lesser than
Poisson distribution. Further, the probabilities found in part (b) are more accurate than
computed in part (c).

Question 2
Mean μ=65
Standard deviation σ =5
Normal distribution
(a) % of eggs have weight above 70 grams P(X>70)
z= 70−65
5 =1
z=1
P ( X >70 ) =P ( Z>1 ) =0.1562(¿ standard normal table)
Hence, 15.92% of eggs have weight above 70 grams.
(b) % of eggs have scores between 70 and 75 grams
P ( 70< X <75 )=P ( 70−65
5 < Z< 75−65
5 )
P ( 70< X <75 ) =P ( 1< Z <2 ) =0.977−84.13
P ( 70< X <75 ) =0.1359(¿ standard normal table)
Hence, 13.59% of eggs have scores between 70 and 75 grams.
(c) Lowest weight of heaviest 5% egg
The p value = 1- 0.05 = 0.95
Z score for P (0.95) =1.645

1.645= x−65
5
x=73.225 grams
(d) Distribution of weight of packs
Each pack has an SRS size of 12
Normal distribution
W N (μ=780 , σ2=300)
(e) Proportion of packs has total weight above 800 grams
Standard deviation = sqrt(300) = 17.32
P ( x> 800 )=P ( ( 800−780 )
17.32 )=P ( Z>1.1547 )=0.1251
Therefore, 0.1251 proportions of packs has total weight above 800 grams.
Question 3
Mean

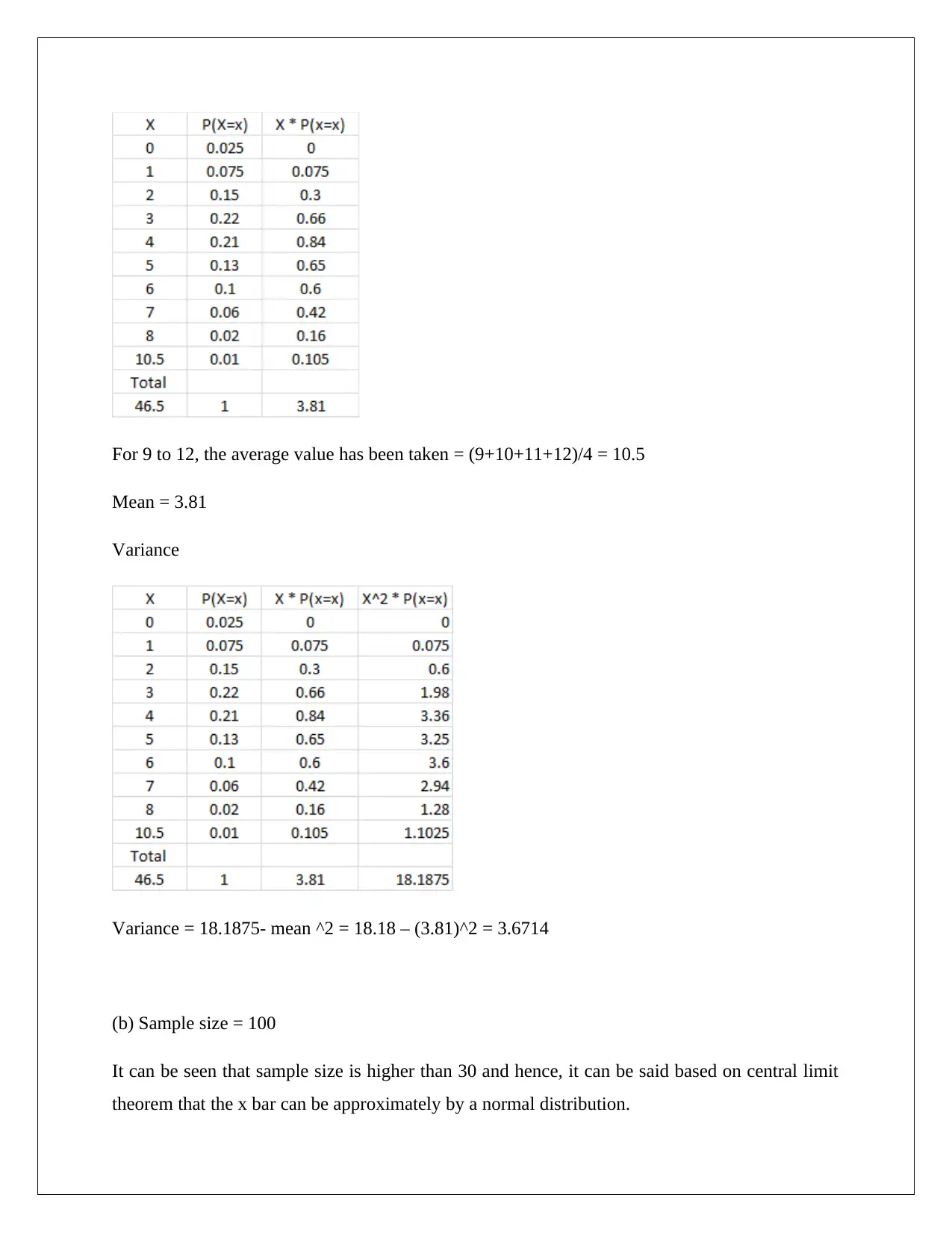
For 9 to 12, the average value has been taken = (9+10+11+12)/4 = 10.5
Mean = 3.81
Variance
Variance = 18.1875- mean ^2 = 18.18 – (3.81)^2 = 3.6714
(b) Sample size = 100
It can be seen that sample size is higher than 30 and hence, it can be said based on central limit
theorem that the x bar can be approximately by a normal distribution.

CLT = X −μ
σ , N ( 0 ,1 ) N →∞
Mean = (1/100)* ∑
i=1
100
E ( x )= 100∗3.81
100 =3.81
Standard deviation = sqrt (3.6714) = 1.914
S.E. = 1.91/ Sqrt(100) = 0.1914
Thus,
X N (3.81 , 0.1914)
(c) Sample size = 100
P ( 3< X < 4 ) =P ( 3−3.81
0.1914 <Z < 4−3.81
0.1914 )=P (−4.23< Z< 0.9926 )=0.8394
P ( 3< X < 4 ) =0.8394
There is a 0.8394 probability that the speed measurement would be between 3 and 4 on the
Beaufort scale.
Question 4
(a) The data is termed as paired data.
(b) Summary statistics

Mean change
Standard deviation
(c) 95% confidence interval
Level of significance = 0.05
Now,
The t value

Now,
Lower limit of 95% confidence interval ¿ Mean difference – t value∗¿
Upper limit of 95% confidence interval ¿ Mean difference +t value∗¿
Therefore, the 95% confidence interval [1.39 10.01] mmHg
(d) Hypotheses testing
H0: μD=0
H1 : μD >0
It can be seen from the above that 0 value does not fall in the 95% confidence interval and hence,
sufficient evidences are present to reject the null hypothesis and to accept the alternative
hypothesis at 5% confidence interval. Thus, it can be concluded that systolic blood pressure has
fallen an hour after the visit of the dentist.
(e) Sample size needs to be determined.
Sample size = (Z value* Standard deviation /margin of error)^2
The z value for 95% confidence = 1.96
Standard deviation = 5 mmHg
Margin of error = 1
Now,
Sample size = (1.96* 5 /1)^2 = 96.04
Therefore, the sample size should be equal to or greater than 97 in order to achieve the mean
change in systolic blood pressure to an accuracy of +/-1 mmHg.

Question 5
(a) There are two situation sleep or no sleep which means it is not a paired situation.
(b) & (c) Summary statistic
For sleep
Mean = 218/10 = 21.8
Standard deviation = sqrt(206.509/10) = 4.6
For no sleep

Mean = 218/9 = 19.22
Standard deviation = sqrt(280.12/9) = 5.74
Pooled standard deviation = sqrt(((8*4.614^2) + (7*5.74^2))/15) =5.17
Null and alternative hypotheses
H0: No difference between the scores of the two groups
H1: difference between the scores of the two groups
The test stat (t value) = ((21.8-19.22)/5.17)* sqrt(1/9 + 1/8) = 1.03
Degree of freedom = 15
∝=0.05
The p value = 0.316
It can be seen that p value is higher than level of significance and hence, null hypotheses would
not be rejected. Therefore, no difference is present between the scores of the two groups.