Statistical Analysis of Health Data - Health Sciences Lab Assignment

This assignment analyzes an article titled "Oral manifestations in diabetic patients under treatment for ischemic heart diseases: A comparative observational study." The student selected this article because it compares oral and dental manifestations in diabetic and non-diabetic patients with ischemic heart disease, focusing on data collection and sampling procedures. The assignment includes frequency distributions of gender, habits, and subjective symptoms, as well as the DMFT score. The student concludes that the DMFT score is highest in the 21-30 group and is normally distributed for non-diabetic patients, but skewed for diabetic patients. The student also discusses alternative data presentation methods, including pie charts and bar graphs, evaluating their pros and cons. Pie charts are easy to interpret but less effective with many variables, while bar graphs can handle large datasets but require additional explanations. The student provides references for all sources used.

Running head: STATISTICAL REASONING FOR HEALTH SCIENCES 1
Statistical Reasoning for Health Sciences
Student Name
Institution

STATISTICAL REASONING FOR HEALTH SCIENCES 2
1.

STATISTICAL REASONING FOR HEALTH SCIENCES 3
2.
I chose the article “Oral manifestations in diabetic patients under treatment for ischemic
heart diseases: A comparative observational study” for this lab for three main reasons. Firstly,
the article is an observational study where oral and dental manifestations for two groups of
patients (non-diabetic and diabetic) receiving different treatment for Ischemic heart disease

STATISTICAL REASONING FOR HEALTH SCIENCES 4
(IHD) are compared. Secondly, the data collection procedures and sampling procedures are what
interested me. The sampling was done randomly for both patients and hospitals, which fives the
research study an upper hand for generalization of the study findings and conclusion.
3.
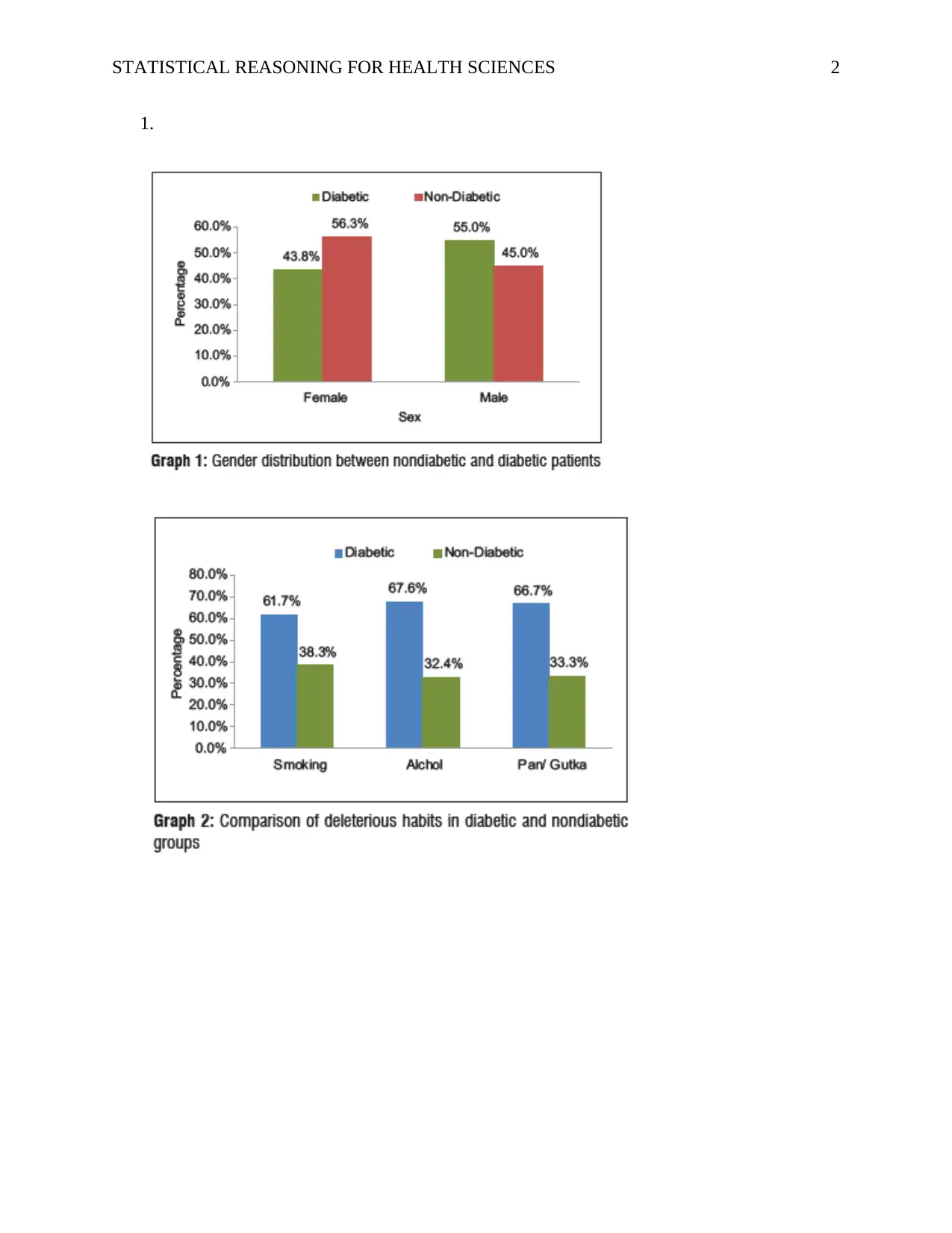
There are three frequency distributions; Gender distribution between non-diabetic and
diabetic patients, Comparison of deleterious habits in diabetic and non-diabetic Groups, and
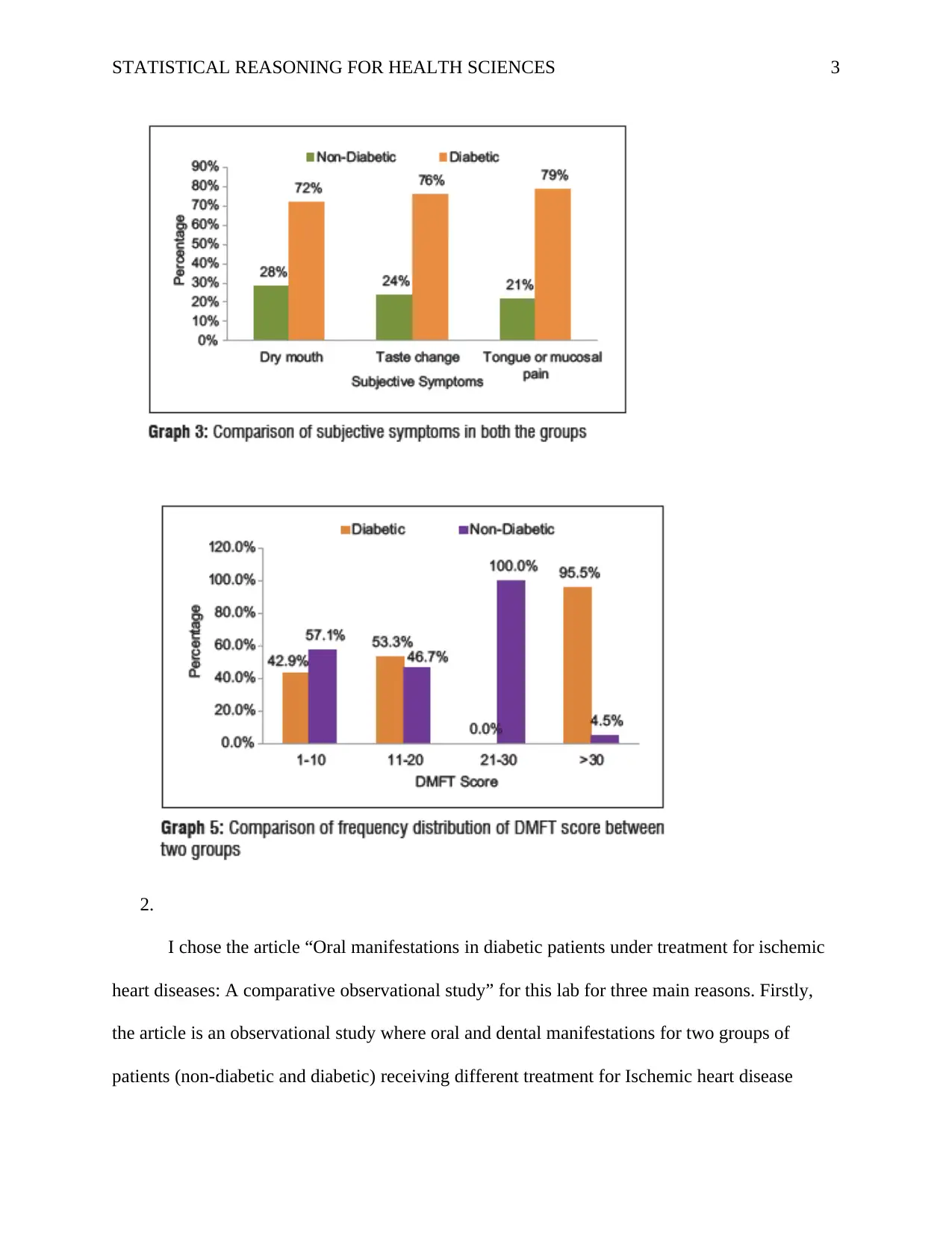
Comparison of subjective symptoms in both the groups. The data of interest in the frequency
distribution between diabetic and non-diabetic is the percentage distribution of diabetic and non-
diabetic males and females. Similarly, the data of interest for frequency distribution plot of the
habits are the prevalence rates of diabetic patients who engage in alcohol consumption, smoking,
Gutka consumption. Lastly, the data of interest for frequency distribution plot of subjective
symptoms is the comparison of prevalence rates for subjective symptoms (dry mouth, change of
taste, and tongue or mucosal pain) for diabetic and non-diabetic patients engage in alcohol
consumption, smoking, and Gutka consumption.
The class size of the frequency distribution plot of DMFT score between groups is 10.
The class size is consistent throughout the frequency plot. From the frequency distribution plot
of DMFT score between groups, we can conclude that DMFT score is highest between 21-30
groups and that the DMFT score for non-diabetic patients is normally distributed with the one
peak at 21-30 group. In contrast, the DMFT score for diabetic patients is skewed to the left.
Moreover, it can be concluded that the DMFT score is relatively equal for groups 1-10 and 11-20
groups.
4.

STATISTICAL REASONING FOR HEALTH SCIENCES 5
The data could also be displayed by the use of pie-charts and bar graph. A pie-chart is a
visual tool used to display data in a circular statistical graph where the circle is divided into
slices where each slice is proportional to the percentage of the variable they represent (Davies,
2017). The total percentage of all slices should sum up to 100%. Data presentation using pie-
charts is simple to construct and easy to read and interpret. A pie chart is an effective tool for
communication in statistics (Coolidge, 2013). Since the pie chart represents data in a visual
graph, it is easy for the both informed and uninformed audience to compare the slices and make a
quick and accurate interpretation. Moreover, pie charts enable readers to make comparisons at a
glance and make an accurate and informed conclusion without any calculation. Lastly, pie charts
are easily manipulated to accommodate information of readers’ interest.
However, data presentation in pie charts has two main disadvantages. A pie chart
becomes less effective when data has many variables. For large data with many slices, the pie
chart becomes overcrowded, and the size of the slices looks equal when they are unequal in the
real sense (Behara & BarCharts, 2014). For instance, it is easier to read, understand, and interpret
a 4-slice pie chart than a 10-slice pie chart because the size of the slices is large enough.
Therefore, pie charts are not effective data presentation tool for large data. Also, pie charts
display charts for a single dataset and not applicable where the comparison of multiple datasets is
required. For multiple datasets, a series of pie charts are required making it hard to compare and
draw conclusions.
Another possible way of presenting data is the use of bar graphs. A bar graph is a visual
chart drawn to compare different categories of data (Stephens, 2011). The bars can either be
vertical or horizontal; however; vertical bar charts are the most common type of bar charts. Bar
charts have two axes; vertical and horizontal axes. For vertical bar charts, the horizontal axis

STATISTICAL REASONING FOR HEALTH SCIENCES 6
displays the categories while the vertical axis displays the frequency or the count. A bar chart is
easy to read and interpret and takes of large volumes of data during data presentation (Spiegel,
Schiller & Srinivasan, 2013). The construction of bar charts is easy as well as its interpretation.
Unlike pie charts, a bar graph can compare small or large values emphatically making it easier
for trend comparison.
Even though the bar chart has more advantages than a pie chart, it has a few
disadvantages. A bar graph is not self-explanatory; therefore, they require additional explanation
(Spiegel & Stephens, 2011). Also, bar charts never highlight key assumptions made during bar
graph drawing and can be manipulated easily to give a false impression.

STATISTICAL REASONING FOR HEALTH SCIENCES 7
References
Behara, R. and BarCharts, I. (2014) Business Statistics. [Boca Raton, FL]: QuickStudy Reference
Guides (Quick Study Business). Available at: http://search.ebscohost.com/login.aspx?
direct=true&db=nlebk&AN=1534295&site=eds-live (Accessed: 24 July 2019).
Coolidge, F. L. (2013) Statistics : A gentle introduction. Sage publ. Available at:
http://search.ebscohost.com/login.aspx?
direct=true&db=cat07375a&AN=glc.N41521&site=eds-live (Accessed: 24 July 2019).
Davies, A. (2017) Understanding Statistics : An Introduction. Washington, D.C.:
Libertarianism.org Press. Available at: http://search.ebscohost.com/login.aspx?
direct=true&db=nlebk&AN=1667844&site=eds-live (Accessed: 24 July 2019).
Spiegel, M., & Stephens, L. (2011). Schaum's outline of theory and problems of statistics. New
York: McGraw Hill Professional.
Spiegel, M., Schiller, J., and Srinivasan, R. (2013). Schaum's outline of probability and statistics.
New York: McGraw-Hill.
Stephens, L. (2011). Statistics for engineers. New York: McGraw-Hill Companies.