Statistics Assignment: Probability, Distributions, and Analysis
VerifiedAdded on 2021/04/16
|8
|1496
|50
Homework Assignment
AI Summary
This statistics assignment solution covers fundamental concepts including probability and frequency distributions, coin tossing scenarios, and probability calculations. It delves into real-world applications using population data from Australia to calculate probabilities, followed by an analysis of labor time using confidence intervals and standard errors. The assignment concludes with a hypothesis testing problem, assessing customer travel distances for a store's advertising strategy, utilizing t-tests to determine whether the average customer lives within a certain radius. This comprehensive solution provides detailed explanations and calculations for each question, including the use of standard deviations, mean values, and confidence levels, demonstrating a strong understanding of statistical principles.

Running head: STATISTICS
Statistics
Name of the Student:
Name of the University:
Author’s note:
Statistics
Name of the Student:
Name of the University:
Author’s note:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1STATISTICS
Table of Contents
Question 1..................................................................................................................................2
1.a) Probability Distribution:.................................................................................................2
1.b) Frequency Distribution:..................................................................................................2
1.c) Coin Tossing:..................................................................................................................3
1.d) Calculation of Probability:..............................................................................................3
Question 2..................................................................................................................................3
Question 3..................................................................................................................................4
3.a)..........................................................................................................................................4
3.b).........................................................................................................................................5
References:.................................................................................................................................7
a.
Table of Contents
Question 1..................................................................................................................................2
1.a) Probability Distribution:.................................................................................................2
1.b) Frequency Distribution:..................................................................................................2
1.c) Coin Tossing:..................................................................................................................3
1.d) Calculation of Probability:..............................................................................................3
Question 2..................................................................................................................................3
Question 3..................................................................................................................................4
3.a)..........................................................................................................................................4
3.b).........................................................................................................................................5
References:.................................................................................................................................7
a.
2STATISTICS
Question 1.
1.a) Probability Distribution:
A probability distribution is a statistical function (f ( x)¿ that indicates all the probable and
likelihood values that a random variable can take within a defined range.
The probability distribution is divided in two ways that are-
Discrete Probability Distribution: It is the probabilistic properties of observable pre-
assigned values. The observable values may either be finite or countably infinite (discrete)
probability distribution. A limited number of probable observations generates discrete
probability distribution. A discrete random variable could be related with a non-zero
probability.
Example: The distribution of errors found per page of a book.
Continuous Probability Distribution: A continuous probability distribution refers the
probabilities of probable values of a continuous random variable. A set of infinite and
uncountable continuous probable values create continuous probability distribution.
Example: The distribution of heights of adult males.
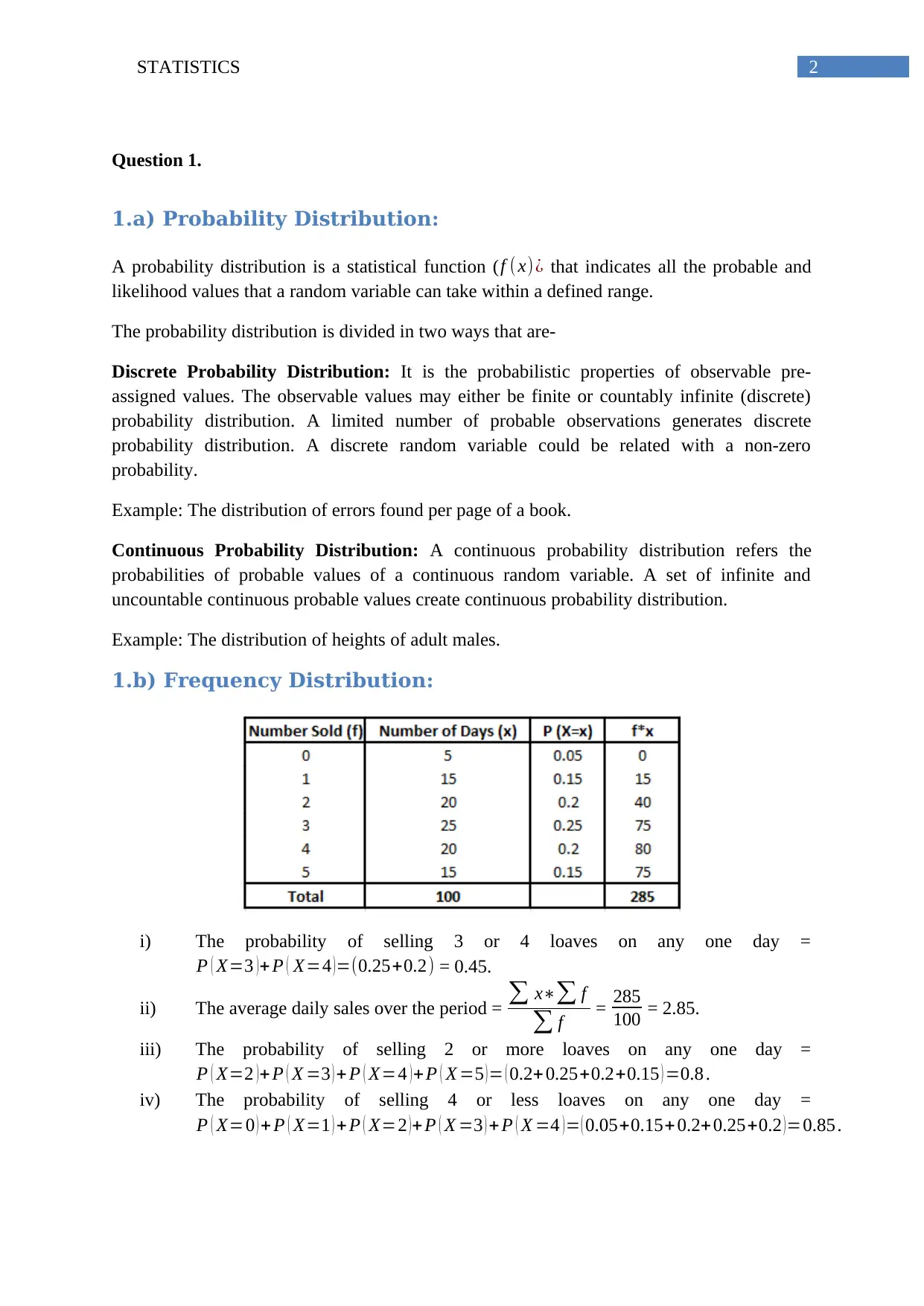
1.b) Frequency Distribution:
i) The probability of selling 3 or 4 loaves on any one day =
P ( X=3 ) + P ( X=4 ) =(0.25+0.2) = 0.45.
ii) The average daily sales over the period = ∑ x∗∑ f
∑ f = 285
100 = 2.85.
iii) The probability of selling 2 or more loaves on any one day =
P ( X=2 )+ P ( X =3 ) + P ( X=4 )+ P ( X =5 )= ( 0.2+ 0.25+0.2+0.15 ) =0.8 .
iv) The probability of selling 4 or less loaves on any one day =
P ( X=0 ) + P ( X=1 ) + P ( X=2 ) + P ( X =3 ) + P ( X =4 ) = ( 0.05+0.15+ 0.2+0.25+0.2 ) =0.85 .
Question 1.
1.a) Probability Distribution:
A probability distribution is a statistical function (f ( x)¿ that indicates all the probable and
likelihood values that a random variable can take within a defined range.
The probability distribution is divided in two ways that are-
Discrete Probability Distribution: It is the probabilistic properties of observable pre-
assigned values. The observable values may either be finite or countably infinite (discrete)
probability distribution. A limited number of probable observations generates discrete
probability distribution. A discrete random variable could be related with a non-zero
probability.
Example: The distribution of errors found per page of a book.
Continuous Probability Distribution: A continuous probability distribution refers the
probabilities of probable values of a continuous random variable. A set of infinite and
uncountable continuous probable values create continuous probability distribution.
Example: The distribution of heights of adult males.
1.b) Frequency Distribution:
i) The probability of selling 3 or 4 loaves on any one day =
P ( X=3 ) + P ( X=4 ) =(0.25+0.2) = 0.45.
ii) The average daily sales over the period = ∑ x∗∑ f
∑ f = 285
100 = 2.85.
iii) The probability of selling 2 or more loaves on any one day =
P ( X=2 )+ P ( X =3 ) + P ( X=4 )+ P ( X =5 )= ( 0.2+ 0.25+0.2+0.15 ) =0.8 .
iv) The probability of selling 4 or less loaves on any one day =
P ( X=0 ) + P ( X=1 ) + P ( X=2 ) + P ( X =3 ) + P ( X =4 ) = ( 0.05+0.15+ 0.2+0.25+0.2 ) =0.85 .
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3STATISTICS
1.c) Coin Tossing:
A coin is tossed twice. The events of flipping the coin two times are independent to
each other. The sample space of two tosses is: Ω = {HH, HT, TH, TT}
The probability of each individual event = P(HH) = P(HT) = P(TH) = P(TT) = 1
4 =0.25 (Due
to independence) (Dudley, 2018).
i) The probability of a head on the first toss = P(HH) + P(HT) = 0.25+0.25 = 0.5
ii) The probability of getting a tail on the second toss given a head on the first toss =
P(HT)= 0.25
iii) The probability of getting two tails in two throws = P (TT) = 0.25.
iv) The probability of getting a tail in first toss and a head on the second toss = P
(TH) = 0.25.
v) The probability of getting a tail on the first and a head on the second or a head on
the first and a tail on the second = P (TH) + P (HT) = (0.25+0.25) = 0.5.
vi) The probability of at least one head on the first two tosses = P (HT) + P (HT) +
P(HH) = (0.25+0.25+0.25) = 0.75.
1.d) Calculation of Probability:
The mean value of sales of apples is 5000.
The value of standard deviation of sales of apples is 600.
Therefore,
The probability of sales that will be greater than 5600 apples =
P ( X >5600) = P ( X – 5000 > 5600-5000) = P ( X -μ>600) = P ( X−μ
600 > 600
600 ) = P ( X−μ
σ >1) =
P (Z>1) = 0.1587 (Ross, 2014).
The probability of sales that will be less than 5240 apples =
P ( X <5240) = P ( X – 5000 < 5240-5000) = P ( X -μ<240) = P ( X−μ
600 < 240
600 ) = P ( X−μ
σ <0.4)
= P (Z<0.4) = 0.6554.
The probability of sales that will be less than 4400 apples =
P ( X <4400) = P ( X – 5000 < 4400-5000) = P ( X -μ < -600) = P ( X−μ
600 < 60 0
−600 ) = P (
X−μ
σ <−1) = P (Z<-1) = 0.1587.
1.c) Coin Tossing:
A coin is tossed twice. The events of flipping the coin two times are independent to
each other. The sample space of two tosses is: Ω = {HH, HT, TH, TT}
The probability of each individual event = P(HH) = P(HT) = P(TH) = P(TT) = 1
4 =0.25 (Due
to independence) (Dudley, 2018).
i) The probability of a head on the first toss = P(HH) + P(HT) = 0.25+0.25 = 0.5
ii) The probability of getting a tail on the second toss given a head on the first toss =
P(HT)= 0.25
iii) The probability of getting two tails in two throws = P (TT) = 0.25.
iv) The probability of getting a tail in first toss and a head on the second toss = P
(TH) = 0.25.
v) The probability of getting a tail on the first and a head on the second or a head on
the first and a tail on the second = P (TH) + P (HT) = (0.25+0.25) = 0.5.
vi) The probability of at least one head on the first two tosses = P (HT) + P (HT) +
P(HH) = (0.25+0.25+0.25) = 0.75.
1.d) Calculation of Probability:
The mean value of sales of apples is 5000.
The value of standard deviation of sales of apples is 600.
Therefore,
The probability of sales that will be greater than 5600 apples =
P ( X >5600) = P ( X – 5000 > 5600-5000) = P ( X -μ>600) = P ( X−μ
600 > 600
600 ) = P ( X−μ
σ >1) =
P (Z>1) = 0.1587 (Ross, 2014).
The probability of sales that will be less than 5240 apples =
P ( X <5240) = P ( X – 5000 < 5240-5000) = P ( X -μ<240) = P ( X−μ
600 < 240
600 ) = P ( X−μ
σ <0.4)
= P (Z<0.4) = 0.6554.
The probability of sales that will be less than 4400 apples =
P ( X <4400) = P ( X – 5000 < 4400-5000) = P ( X -μ < -600) = P ( X−μ
600 < 60 0
−600 ) = P (
X−μ
σ <−1) = P (Z<-1) = 0.1587.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
4STATISTICS
Question 2.
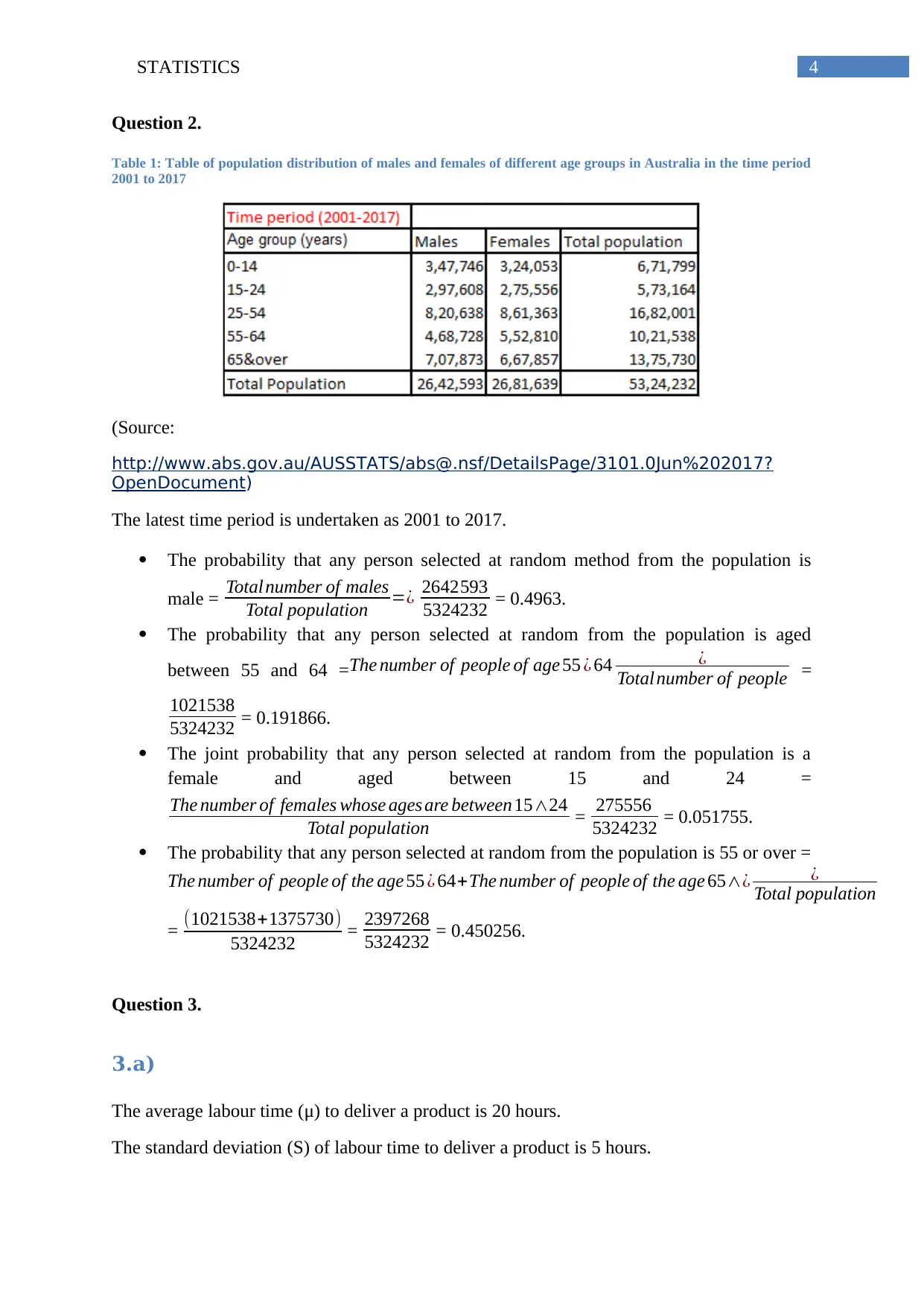
Table 1: Table of population distribution of males and females of different age groups in Australia in the time period
2001 to 2017
(Source:
http://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3101.0Jun%202017?
OpenDocument)
The latest time period is undertaken as 2001 to 2017.
The probability that any person selected at random method from the population is
male = Total number of males
Total population =¿ 2642593
5324232 = 0.4963.
The probability that any person selected at random from the population is aged
between 55 and 64 = The number of people of age 55 ¿ 64 ¿
Total number of people =
1021538
5324232 = 0.191866.
The joint probability that any person selected at random from the population is a
female and aged between 15 and 24 =
The number of females whose ages are between 15∧24
Total population = 275556
5324232 = 0.051755.
The probability that any person selected at random from the population is 55 or over =
The number of people of the age 55 ¿ 64+The number of people of the age 65∧¿ ¿
Total population
= (1021538+1375730)
5324232 = 2397268
5324232 = 0.450256.
Question 3.
3.a)
The average labour time (μ) to deliver a product is 20 hours.
The standard deviation (S) of labour time to deliver a product is 5 hours.
Question 2.
Table 1: Table of population distribution of males and females of different age groups in Australia in the time period
2001 to 2017
(Source:
http://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3101.0Jun%202017?
OpenDocument)
The latest time period is undertaken as 2001 to 2017.
The probability that any person selected at random method from the population is
male = Total number of males
Total population =¿ 2642593
5324232 = 0.4963.
The probability that any person selected at random from the population is aged
between 55 and 64 = The number of people of age 55 ¿ 64 ¿
Total number of people =
1021538
5324232 = 0.191866.
The joint probability that any person selected at random from the population is a
female and aged between 15 and 24 =
The number of females whose ages are between 15∧24
Total population = 275556
5324232 = 0.051755.
The probability that any person selected at random from the population is 55 or over =
The number of people of the age 55 ¿ 64+The number of people of the age 65∧¿ ¿
Total population
= (1021538+1375730)
5324232 = 2397268
5324232 = 0.450256.
Question 3.
3.a)
The average labour time (μ) to deliver a product is 20 hours.
The standard deviation (S) of labour time to deliver a product is 5 hours.

5STATISTICS
The number of random samples (n) as per observation = 64.
It is assumed that labour time is normally distributed.
The standard error is calculated as: SE = S
√ n = 5
√64 = 5
8 = 0.625 hours (Rohatgi and Saleh,
2015).
The value of t-critical at 95% confidence interval is = 1.96.
The Upper control limit of the average labour time (μ) is given as: (μ + t*SE) = (20 +
1.96*0.625) hours = (20 + 1.225) hours = 21.225 hours.
The Lower control limit of the average labour time (μ) is given as: (μ - t*SE) = (20 -
1.96*0.625) hours = (20 - 1.225) hours = 18.775 hours.
If management wishes to use smaller samples of 16 observations, then n =16.
The standard error would be calculated as: SE = S
√n = 5
√16 = 5
4 = 1.25 hours.
The Upper control limit of the average labour time (μ) is given as: (μ + t*SE) = (20 +
1.96*1.25) hours = (20 + 2.45) hours = 22.45 hours.
The Lower control limit of the average labour time (μ) is given as: (μ - t*SE) = (20 -
1.96*1.625) hours = (20 - 2.45) hours = 17.55 hours.
3.b)
Argon advertising Agency has suggested to store that it use mail circulars for the area within
a 15 km radius of its store.
The owner of Speciality store claims that average customer lives no more than 9 km from the
store.
A sample of 50 customers indicates mean travelling distance of 10.22 km.
The assumed level of significance for hypothesis testing = 0.05.
Experience shows that the average travelling distance = 5 km.
Hypotheses:
Null hypothesis (H0): Average customer lives no more than (equal to) 9 km from the store.
Alternative hypothesis (HA): Average customer lives more than 9 km from the store.
Calculation:
We apply one-sample t-test for hypothesis testing.
The number of random samples (n) as per observation = 64.
It is assumed that labour time is normally distributed.
The standard error is calculated as: SE = S
√ n = 5
√64 = 5
8 = 0.625 hours (Rohatgi and Saleh,
2015).
The value of t-critical at 95% confidence interval is = 1.96.
The Upper control limit of the average labour time (μ) is given as: (μ + t*SE) = (20 +
1.96*0.625) hours = (20 + 1.225) hours = 21.225 hours.
The Lower control limit of the average labour time (μ) is given as: (μ - t*SE) = (20 -
1.96*0.625) hours = (20 - 1.225) hours = 18.775 hours.
If management wishes to use smaller samples of 16 observations, then n =16.
The standard error would be calculated as: SE = S
√n = 5
√16 = 5
4 = 1.25 hours.
The Upper control limit of the average labour time (μ) is given as: (μ + t*SE) = (20 +
1.96*1.25) hours = (20 + 2.45) hours = 22.45 hours.
The Lower control limit of the average labour time (μ) is given as: (μ - t*SE) = (20 -
1.96*1.625) hours = (20 - 2.45) hours = 17.55 hours.
3.b)
Argon advertising Agency has suggested to store that it use mail circulars for the area within
a 15 km radius of its store.
The owner of Speciality store claims that average customer lives no more than 9 km from the
store.
A sample of 50 customers indicates mean travelling distance of 10.22 km.
The assumed level of significance for hypothesis testing = 0.05.
Experience shows that the average travelling distance = 5 km.
Hypotheses:
Null hypothesis (H0): Average customer lives no more than (equal to) 9 km from the store.
Alternative hypothesis (HA): Average customer lives more than 9 km from the store.
Calculation:
We apply one-sample t-test for hypothesis testing.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

6STATISTICS
Sample mean (μ) of distance of 50 customers = 9 km.
Population mean ( X ) distance = 10.22 km.
Standard deviation (S) in terms of experience = 5 km.
Number of samples (n) = 50.
Standard error of distance = SE = S
√ n = 5
√50 =¿ 0.707 hours.
The level of significance = 0.05.
The t-statistic at 5% level of significance = 1.96.
The calculated t-statistic =
( X−μ)
S
√n
=
(10.22−9)
5
√50
= 1.22
0.707 = 1.7253.
Decision Making:
As, tcric > tcal (1.7253<1.96), therefore, we cannot reject the null hypothesis at 5% level of
significance.
It could be concluded that average customer lives no more than 9 km. from the store with 5%
probability (Zhao, 2015).
Hence, the claim of Argon’s representative is found to be true.
Sample mean (μ) of distance of 50 customers = 9 km.
Population mean ( X ) distance = 10.22 km.
Standard deviation (S) in terms of experience = 5 km.
Number of samples (n) = 50.
Standard error of distance = SE = S
√ n = 5
√50 =¿ 0.707 hours.
The level of significance = 0.05.
The t-statistic at 5% level of significance = 1.96.
The calculated t-statistic =
( X−μ)
S
√n
=
(10.22−9)
5
√50
= 1.22
0.707 = 1.7253.
Decision Making:
As, tcric > tcal (1.7253<1.96), therefore, we cannot reject the null hypothesis at 5% level of
significance.
It could be concluded that average customer lives no more than 9 km. from the store with 5%
probability (Zhao, 2015).
Hence, the claim of Argon’s representative is found to be true.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

7STATISTICS
References:
Dudley, R. M. (2018). Real analysis and probability. CRC Press.
Rohatgi, V. K., & Saleh, A. M. E. (2015). An introduction to probability and statistics. John
Wiley & Sons.
Ross, S. M. (2014). Introduction to probability models. Academic press.
Zhao, Y. (2015). Data mining techniques.
References:
Dudley, R. M. (2018). Real analysis and probability. CRC Press.
Rohatgi, V. K., & Saleh, A. M. E. (2015). An introduction to probability and statistics. John
Wiley & Sons.
Ross, S. M. (2014). Introduction to probability models. Academic press.
Zhao, Y. (2015). Data mining techniques.
1 out of 8
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





