Statistics Assignment: Regression, Hypothesis, and Indexes

This statistics assignment presents solutions to two main questions. The first question involves a regression model, explaining the computation of seasonal indexes and their application in business decision-making, particularly in forecasting and performance analysis. The second question focuses on hypothesis testing, including the calculation of a z-value, p-value, and the probability of a Type II error, concluding that the average score on an exam at the University of Adelaide is significantly higher than the national average. The document provides detailed steps, calculations, and explanations, along with relevant references to support the analysis and findings.

STATISTICS
Assignment
[Pick the date]
Student Name

Question 1
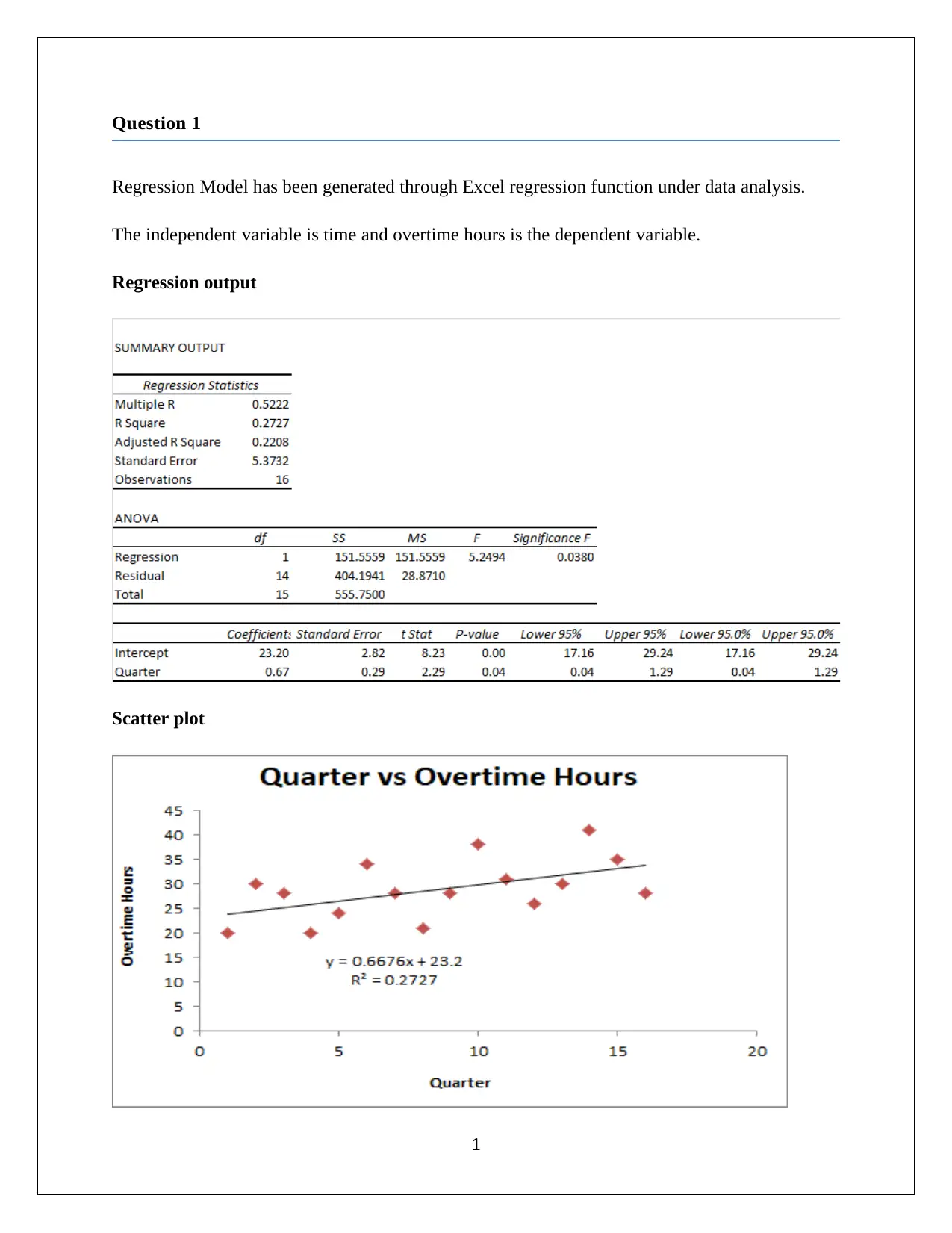
Regression Model has been generated through Excel regression function under data analysis.
The independent variable is time and overtime hours is the dependent variable.
Regression output
Scatter plot
1

(a) Regression line equation
y=23.20+ ( 0.67 ) ×t
Overtime hours=23.20+ ( 0.67 )∗Time
b) The computation of the seasonal indexes on the basis of the above regression line consists of
different steps outlined below (Hillier, 2016).
Step 1: The predicted value of overtime hours or y needs to be estimated using the regression
equation obtained above for all values of independent variable i.e. time.
Step 2: The ratio of actual value of overtime hours and predicted value of the same needs to be
estimated for each of the quarters.
Step 3: The quarterly average is ascertained and adjustment is made based on which seasonal
indexes are derived.
c) Introduction
A number of business tend to be seasonal in nature i.e. the underlying financial performance is
dependent on the particular seasons. As a result, the various aspects related to the business would
2

follow a seasonal trend. An example in this regards would be the hotel industry which tend to
have lean season and peak season and the financial performance also is dictated by these seasons
(Hair et. al., 2015). To represent these seasonal trends, seasonal indexes are critical as they
estimate the seasonal impact on the business and allows it to plan accordingly. In this backdrop,
the given report aims to indicate the connection between seasonal indexes and business decision
making.
Discussion
Seasonal indexes can facilitate business decision making in the following aspects.
Forecasting
Businesses need to plan for the future keeping into consideration the empirical performance of
the business. The seasonal indexes tend to represent the empirical business trends which can
enable the managers to estimate or forecast the future demand. This is pivotal since these
seasonal trends can be significant in estimation of demand and predicting whether the capacity
available would suffice to meet the estimated demand especially in the peak season. A key
decision that the management would need to take is whether to add incremental capacity to serve
the expected incremental demand in the future (Hastie, Tibshirani and Friedman, 2011).
However, the above decision is easier said than done especially for businesses for strong
seasonal trends. This is because the demand peaks out in one season while slack exists in the
other season. Hence, addition of incremental capacity is not always advisable since on an annual
basis, the capacity utilisation is not 100%. Therefore, manufacturing is usually outsourced and
these contracts have to be worked out in advance which is possible only with accurate
forecasting in which case seasonal indexes are vital (Hair et. al., 2015). Additional use of
seasonal indexes is with regards to capital budgeting where estimated sales in the future need to
be estimated so as to evaluate whether to undertake a given expansion or not. If the estimates of
sales or their precise pattern is not estimated with precision, then the investment could be
jeopardised and hence management relies on precise estimation of seasonal indexes (Flick,
2015).
Business Performance Analysis
3

The analysis of performance of business also requires that the seasonal trends should be
identified and then using the seasonal indexed, this must be deseasonalised so that the business
performance net of the seasonal effect can be witnessed. This is imperative since there is a
tendency to estimate the peak as superior performance and lean seasons as inferior performance.
But, it can be possible that the business performance in the peak season may infact be inferior
while in the lean season, it might be superior. To explore the business performance, the
management relies on these seasonal indexes. Also, these are used to fixed future targets which
form basis for performance management (Hastie, Tibshirani and Friedman, 2011).
Conclusion
The discussion above clearly highlights that vital information is provided by seasonal indexes
particularly for businesses where the seasonal impact is significant. For future growth and
forecasting, the management tends to rely on these seasonal indexes as these tend to enhance the
accuracy of the forecasts and thereby promote prudent decision making particularly in meeting
incremental demand. Further, seasonal indexes are also useful for critically analysing the
performance of the business which may be confusing otherwise and hence may yield incorrect
conclusions.
Question 2
Sample size = 25
Mean = 1375
Standard deviation (population) =125
Part a
Null hypothesis Ho : μ=1300 Average score on an exam in University of Adelaide is not higher
than the national average of 1300.
Alternative hypothesis H1 :μ >1300 Average score on an exam in University of Adelaide
significantly higher than the national average of 1300.
4

Part b
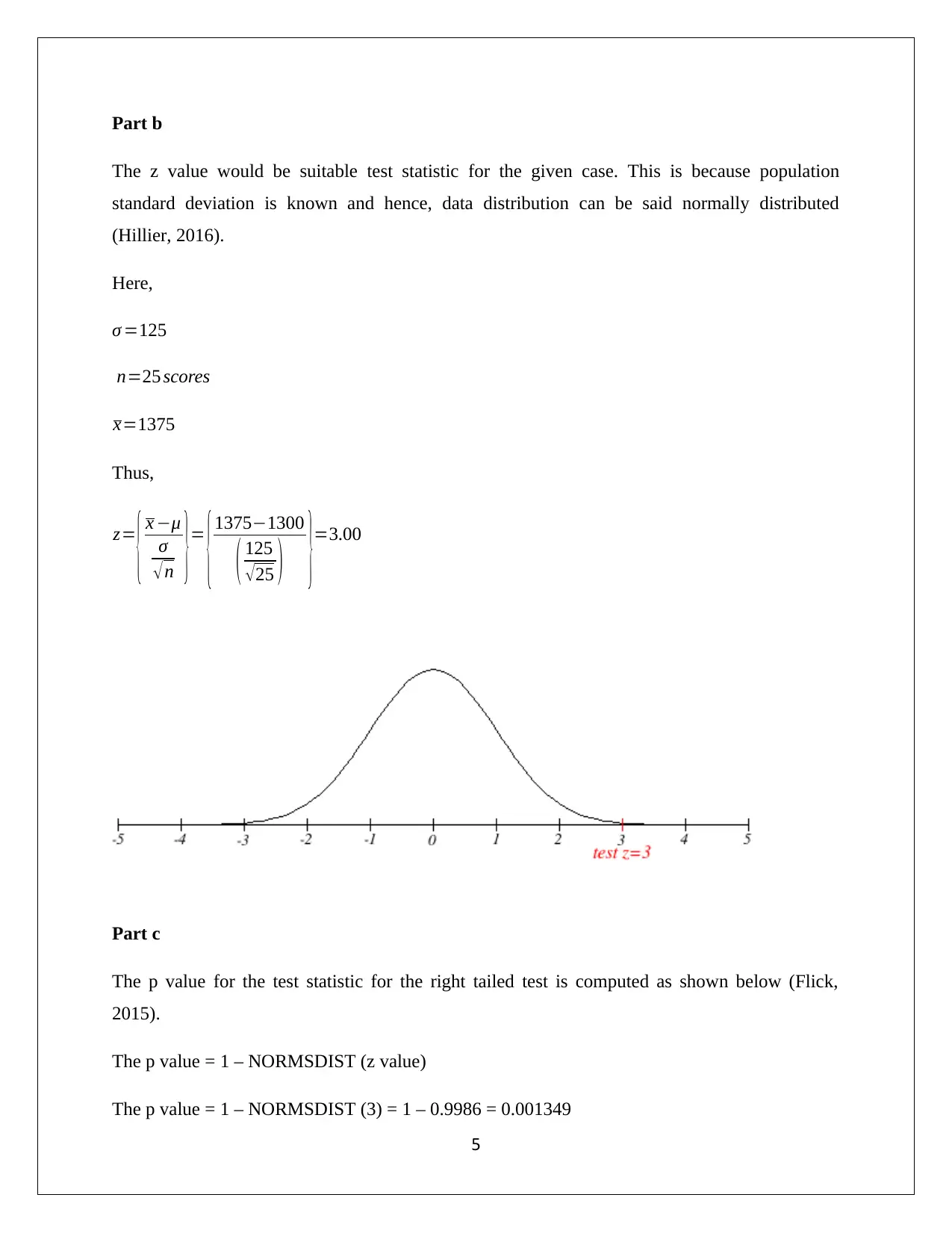
The z value would be suitable test statistic for the given case. This is because population
standard deviation is known and hence, data distribution can be said normally distributed
(Hillier, 2016).
Here,
σ =125
n=25 scores
x=1375
Thus,
z=
{ x −μ
σ
√ n }=
{1375−1300
( 125
√25 ) }=3.00
Part c
The p value for the test statistic for the right tailed test is computed as shown below (Flick,
2015).
The p value = 1 – NORMSDIST (z value)
The p value = 1 – NORMSDIST (3) = 1 – 0.9986 = 0.001349
5

The p value corresponding to z value and right tailed hypothesis testing is 0.001349.
Part d
Let the significance level = 5%
It is apparent that p value is lesser than the significance level (0.001349 <0.05). Hence, sufficient
proof is available for the rejection of null hypothesis. As a result, alternative hypothesis will be
accepted (Eriksson and Kovalainen, 2015). Therefore, average score on the exam in University
of Adelaide is significantly higher than the national average of 1300.
(ii) Computation of probability of type II error
Ho : μ=50
Ha : μ>50
μ=55, σ =1 , n=16 , ∝=0.05
For the calculation of probability of type II error, rejection region would be an imperative aspect.
RR= { x : z > z0.05 }
z0.05=1.645
z= x−50
10
√ 16
Hence,
x−50
10
√16
=1.645
x=54.11
6

Probability of type II error
p=P
( z< 54.11−55
( 10
√ 16 ) )
p=P ( z < (−0.35 ) )
p=NORMSDIST (−0.35)
p=0.3612
Hence, the 0.3612 is the probability of type II error for the given hypothesis.
References
7

Eriksson, P. and Kovalainen, A. (2015) Quantitative methods in business research (3rd ed.).
London: Sage Publications.
Flick, U. (2015) Introducing research methodology: A beginner's guide to doing a research
project (4th ed.). New York: Sage Publications.
Hair, J. F., Wolfinbarger, M., Money, A. H., Samouel, P., and Page, M. J. (2015) Essentials of
business research methods (2nd ed.). New York: Routledge.
Hastie, T., Tibshirani, R. and Friedman, J. (2011) The Elements of Statistical Learning (4th
ed.). New York: Springer Publications.
Hillier, F. (2016) Introduction to Operations Research (6th ed.). New York: McGraw Hill
Publications.
8