Statistics Assignment: Confidence Intervals & Hypothesis Testing

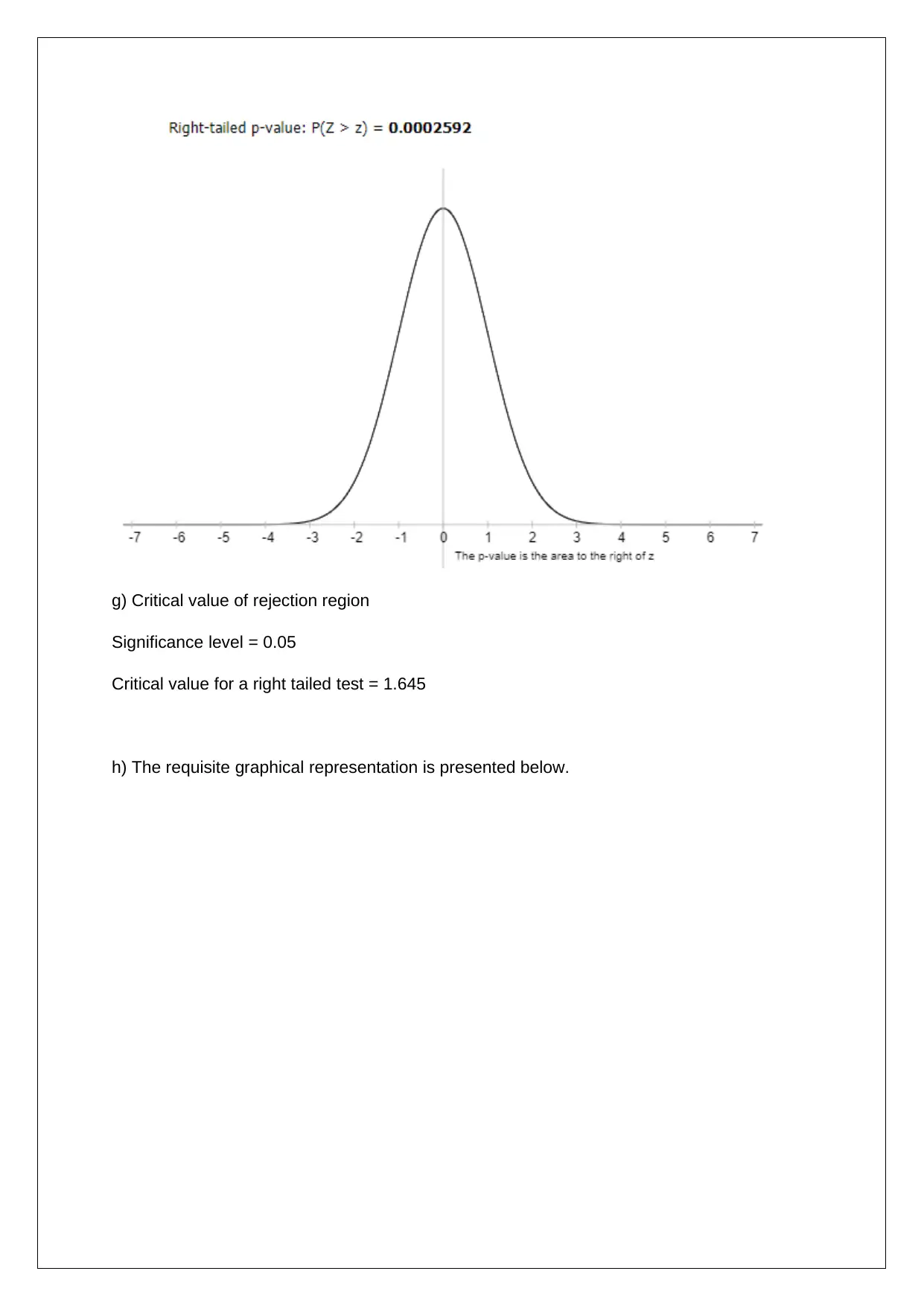
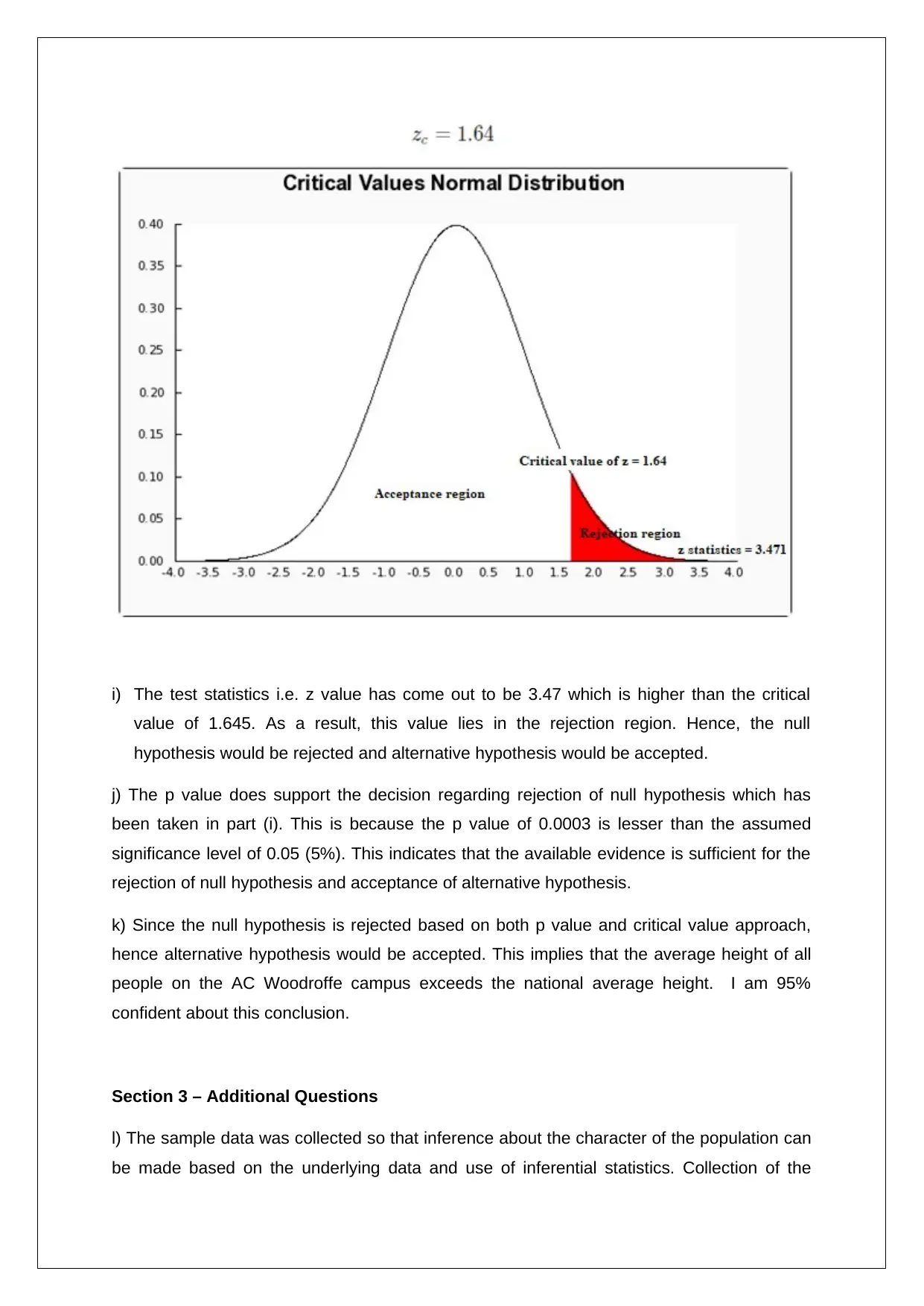
This statistics assignment provides a comprehensive analysis of height data using confidence intervals and hypothesis testing. The solution includes the interpretation of 90%, 95%, and 99% confidence intervals, evaluating the impact of sample size on the accuracy of population mean estimates. The assignment delves into hypothesis testing, formulating null and alternative hypotheses regarding the average height of individuals on the Woodroffe campus compared to the national average. It calculates the z-statistic and p-value, determines the critical value for rejection regions, and provides a graphical representation of the hypothesis test. The solution demonstrates how to reject the null hypothesis based on both the p-value and critical value approaches, concluding that the average height on the Woodroffe campus exceeds the national average with 95% confidence. Additionally, the assignment explains the rationale behind using inferential statistics with sample data and emphasizes the importance of random sampling to avoid bias and ensure a representative sample. The solution justifies the use of z-statistics over t-statistics due to the large sample size, aligning with the Central Limit Theorem. Overall, the assignment offers a detailed statistical analysis, covering key concepts and methodologies for data interpretation and hypothesis validation.

STATISTICS
STUDENT ID:
[Pick the date]

Section 1
a) (163.41,166.59)
Interpretation: 90% confidence interval indicates we are 90% confident enough that the true
average belongs within the lower limit and the upper limit of the 90% confidence interval.
b) (175.731,179.869)
Interpretation: it indicates are 95% confident enough that the true male average height
belongs between 175.731 inch and 179.869 inch
c) (169.085,173.915)
Interpretation: it indicates are 99%
No because we need to increase the sample size to get better estimate of the population
mean height of both genders. 113 sample size is very less as compared to the whole
campus.
Section 2 (Hypothesis Testing)
On an average the people on Woodroffe campus are taller than the national average.
d) Null hypothesis
H0 : μ=168.3 The average height of all people at Woodroffe campus is equal to the national
average of 168.3 cm.
e) Alternate hypothesis
Ha : μ>168.3 The average height of all people at Woodroffe campus is more than the
national average of 168.3 cm.
f) The z statistics and p value
z statistics= x−μ
s
√ n
= 171.5−168.3
9.8
√ 113
=3.4711
From the sign of alternative hypothesis, it can be said that it is a right-tailed hypothesis
testing.
The p value corresponding to z value = 0.000259

g) Critical value of rejection region
Significance level = 0.05
Critical value for a right tailed test = 1.645
h) The requisite graphical representation is presented below.

i) The test statistics i.e. z value has come out to be 3.47 which is higher than the critical
value of 1.645. As a result, this value lies in the rejection region. Hence, the null
hypothesis would be rejected and alternative hypothesis would be accepted.
j) The p value does support the decision regarding rejection of null hypothesis which has
been taken in part (i). This is because the p value of 0.0003 is lesser than the assumed
significance level of 0.05 (5%). This indicates that the available evidence is sufficient for the
rejection of null hypothesis and acceptance of alternative hypothesis.
k) Since the null hypothesis is rejected based on both p value and critical value approach,
hence alternative hypothesis would be accepted. This implies that the average height of all
people on the AC Woodroffe campus exceeds the national average height. I am 95%
confident about this conclusion.
Section 3 – Additional Questions
l) The sample data was collected so that inference about the character of the population can
be made based on the underlying data and use of inferential statistics. Collection of the

population would be time consuming and also would require a lot of effort which is not
always feasible. Thus, a superior alternative is to collect a representative sample and make
inference about the population using techniques provided under inferential statistics.
m) It is importantly to select the test subjects randomly so as to avoid bias and ensure that
the selected sample is representative of the underlying population. Also, a random selection
ensures that there is equal chance provided to each of the constituents of the population to
be selected in the sample. This would not be possible without random sampling and as a
result would not be representative of the population of interest.
n) In the given case, z statistics has been preferred over t statistics since the sample size if
quite large. As per Central Limit Theorem, if the sample size is greater than 30, then the
underlying distribution can be assumed to be normal. Owing to normal distribution, it is
appropriate to use the z statistics instead of t statistics.