Holmes Institute HI6007 Statistics for Business Decisions Report

This report presents a statistical analysis of business decisions, encompassing various aspects of data interpretation and application. The assignment includes an examination of Australian food and fiber exports, comparing values and percentages across different states in 2010 and 2015. It also features a frequency distribution analysis with relative and cumulative frequencies. Furthermore, the report delves into the relationship between the rate of inflation and the All-Ordinaries Index in Australia from 1995 to 2015, including descriptive statistics, correlation coefficients, and a simple linear regression model. The analysis assesses the influence of inflation on the stock market index, evaluating the model's fit and the significance of the findings, along with relevant references.

Running head: STATISTICS FOR BUSINESS DECISIONS
Statistics for Business
Name of the Student:
Name of the University:
Author note:

1STATISTICS FOR BUSINESS DECISIONS
Table of Contents
Answer 1..........................................................................................................................................2
Answer 2..........................................................................................................................................4
Answer 3..........................................................................................................................................6
References......................................................................................................................................12

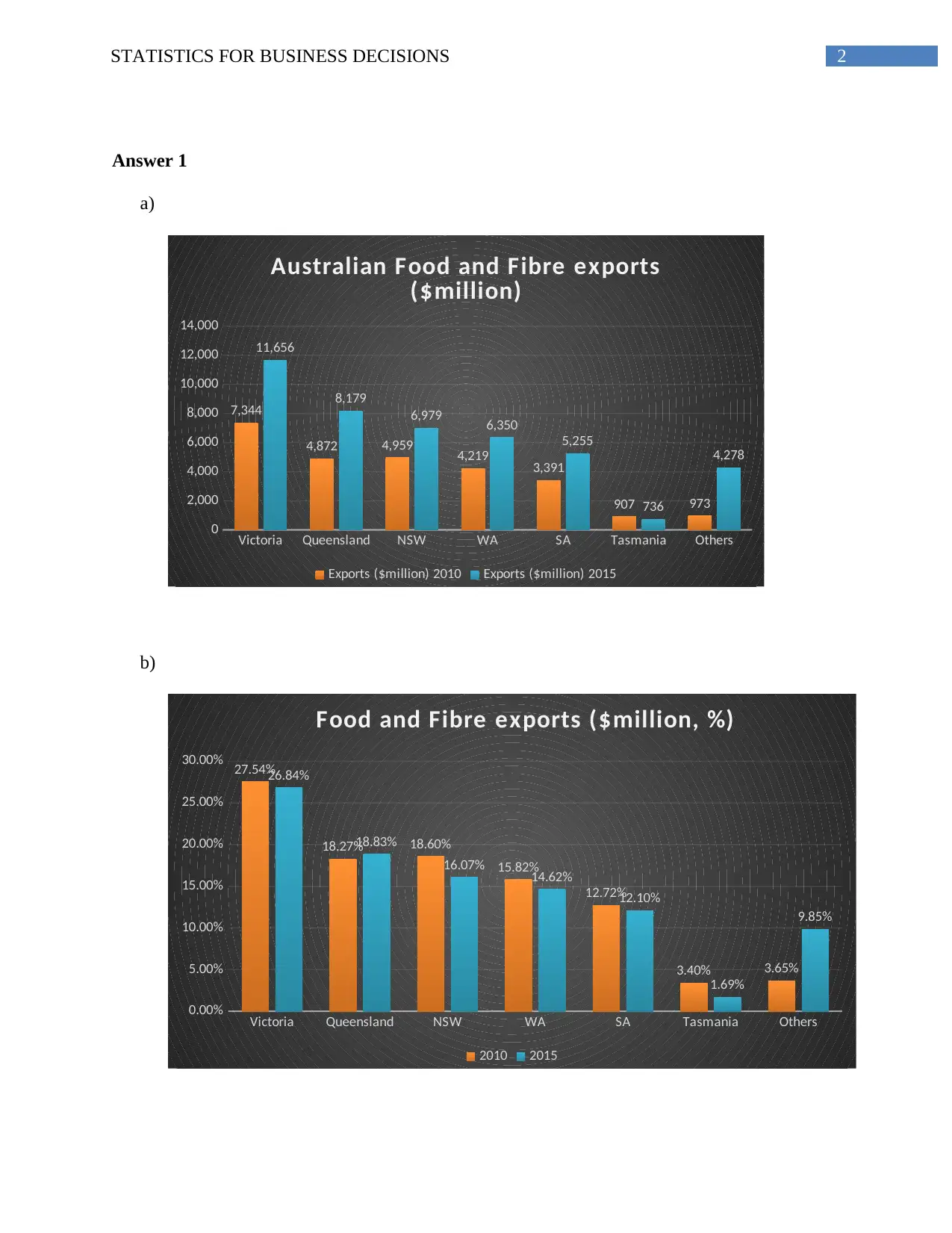
2STATISTICS FOR BUSINESS DECISIONS
Answer 1
a)
Victoria Queensland NSW WA SA Tasmania Others
0
2,000
4,000
6,000
8,000
10,000
12,000
14,000
7,344
4,872 4,959 4,219 3,391
907 973
11,656
8,179
6,979 6,350
5,255
736
4,278
Australian Food and Fibre exports
($million)
Exports ($million) 2010 Exports ($million) 2015
b)
Victoria Queensland NSW WA SA Tasmania Others
0.00%
5.00%
10.00%
15.00%
20.00%
25.00%
30.00% 27.54%
18.27% 18.60%
15.82%
12.72%
3.40% 3.65%
26.84%
18.83%
16.07% 14.62%
12.10%
1.69%
9.85%
Food and Fibre exports ($million, %)
2010 2015

3STATISTICS FOR BUSINESS DECISIONS
c) The two graphs above represent the comparison of the Australian food and fibre exports
in $million and in percentage for 2010 and 2015, broken down by the states. Both the
charts show that the total value of food and fibre exports has been remarkably good in
Victoria in both the years compared to the other states of Australia. The first chart
represents substantial increase in the total value of exports from 2010 to 2015 for all the
Australian states. The value of food and fibre export is highest in Victoria, which is
followed by the other states, namely, Queensland, NSW, WA, SA, and Tasmania. Export
value is slightly higher in ‘Others’ category, than in Tasmania. Both the years, 2010 and
2015, saw similar trends in exports across all the states.
The percentage values of export represent the input of these Australian states in
the total exports value of the food and fibre for both 2010 and 2015. The total export
value has increased in 2015 than in 2010, which also changes the proportion of
contribution made by the states. It shows that, due to the higher proportion or percentage
of contribution in 2010 than in 2015, the performance of all the states were better in 2010
compared to that in 2015.

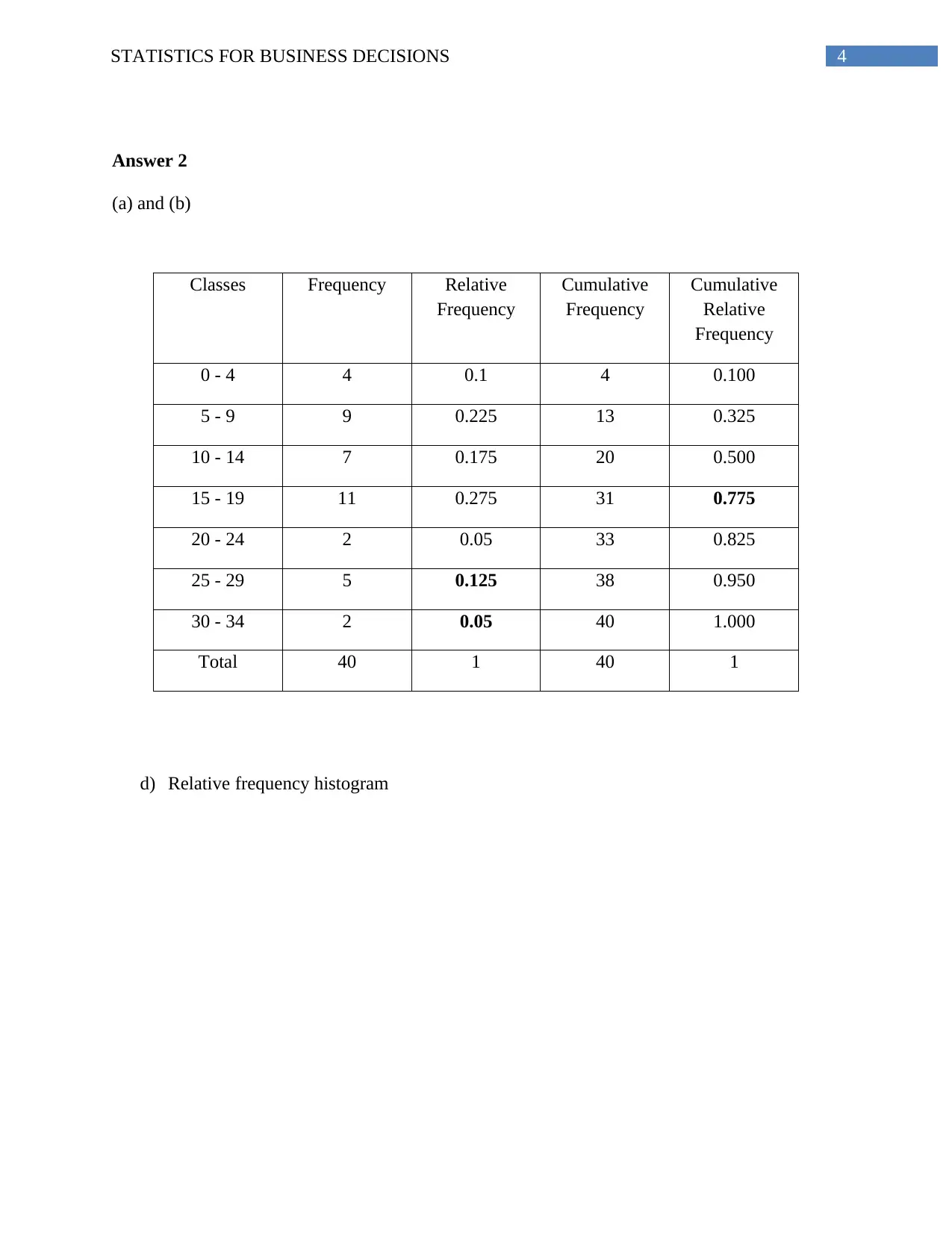
4STATISTICS FOR BUSINESS DECISIONS
Answer 2
(a) and (b)
Classes Frequency Relative
Frequency
Cumulative
Frequency
Cumulative
Relative
Frequency
0 - 4 4 0.1 4 0.100
5 - 9 9 0.225 13 0.325
10 - 14 7 0.175 20 0.500
15 - 19 11 0.275 31 0.775
20 - 24 2 0.05 33 0.825
25 - 29 5 0.125 38 0.950
30 - 34 2 0.05 40 1.000
Total 40 1 40 1
d) Relative frequency histogram

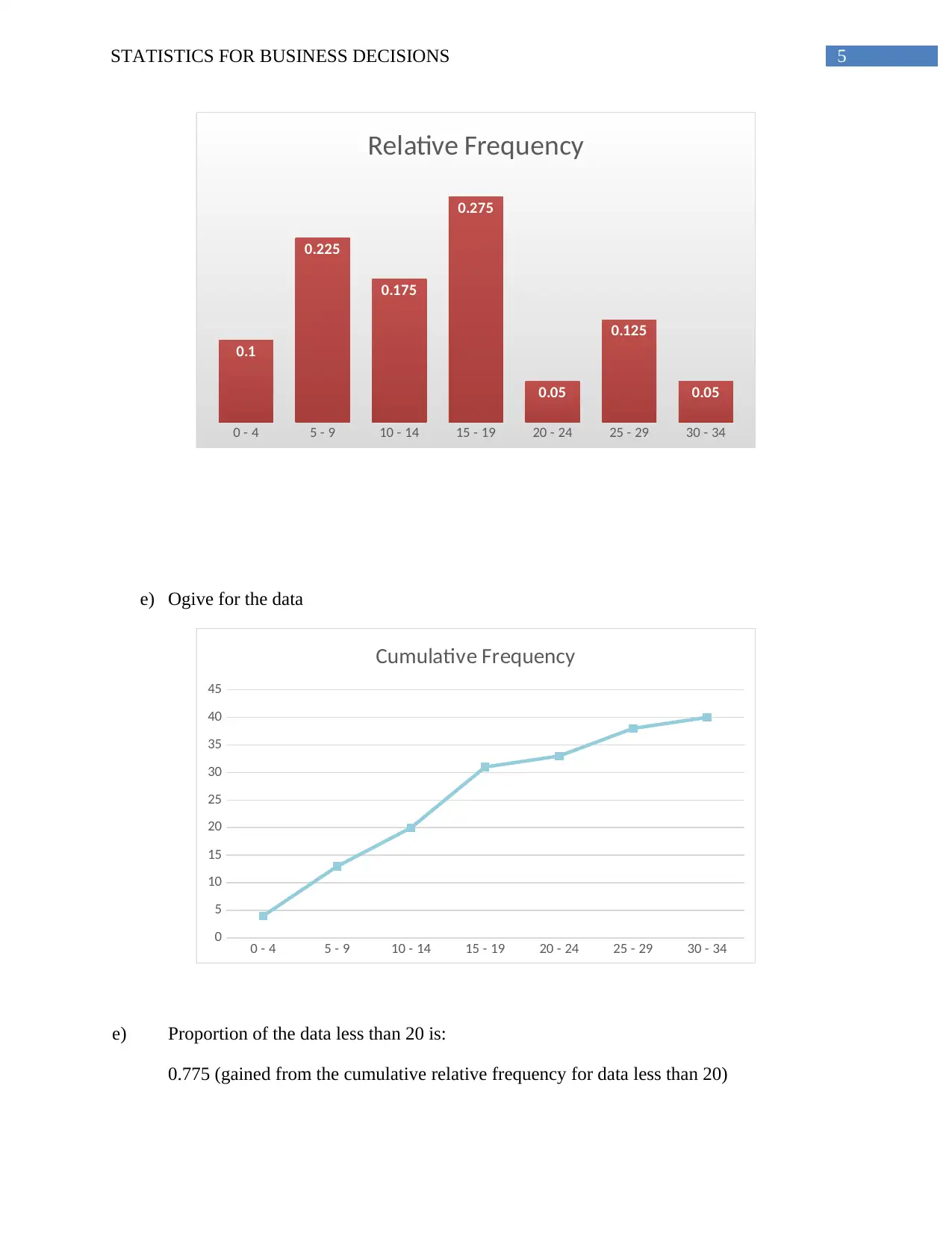
5STATISTICS FOR BUSINESS DECISIONS
0 - 4 5 - 9 10 - 14 15 - 19 20 - 24 25 - 29 30 - 34
0.1
0.225
0.175
0.275
0.05
0.125
0.05
Relative Frequency
e) Ogive for the data
0 - 4 5 - 9 10 - 14 15 - 19 20 - 24 25 - 29 30 - 34
0
5
10
15
20
25
30
35
40
45
Cumulative Frequency
e) Proportion of the data less than 20 is:
0.775 (gained from the cumulative relative frequency for data less than 20)

6STATISTICS FOR BUSINESS DECISIONS
f) Proportion of the data more than 24 is:
1 – 0.825 = 0.175 (gained from the cumulative relative frequency for data more than 24)

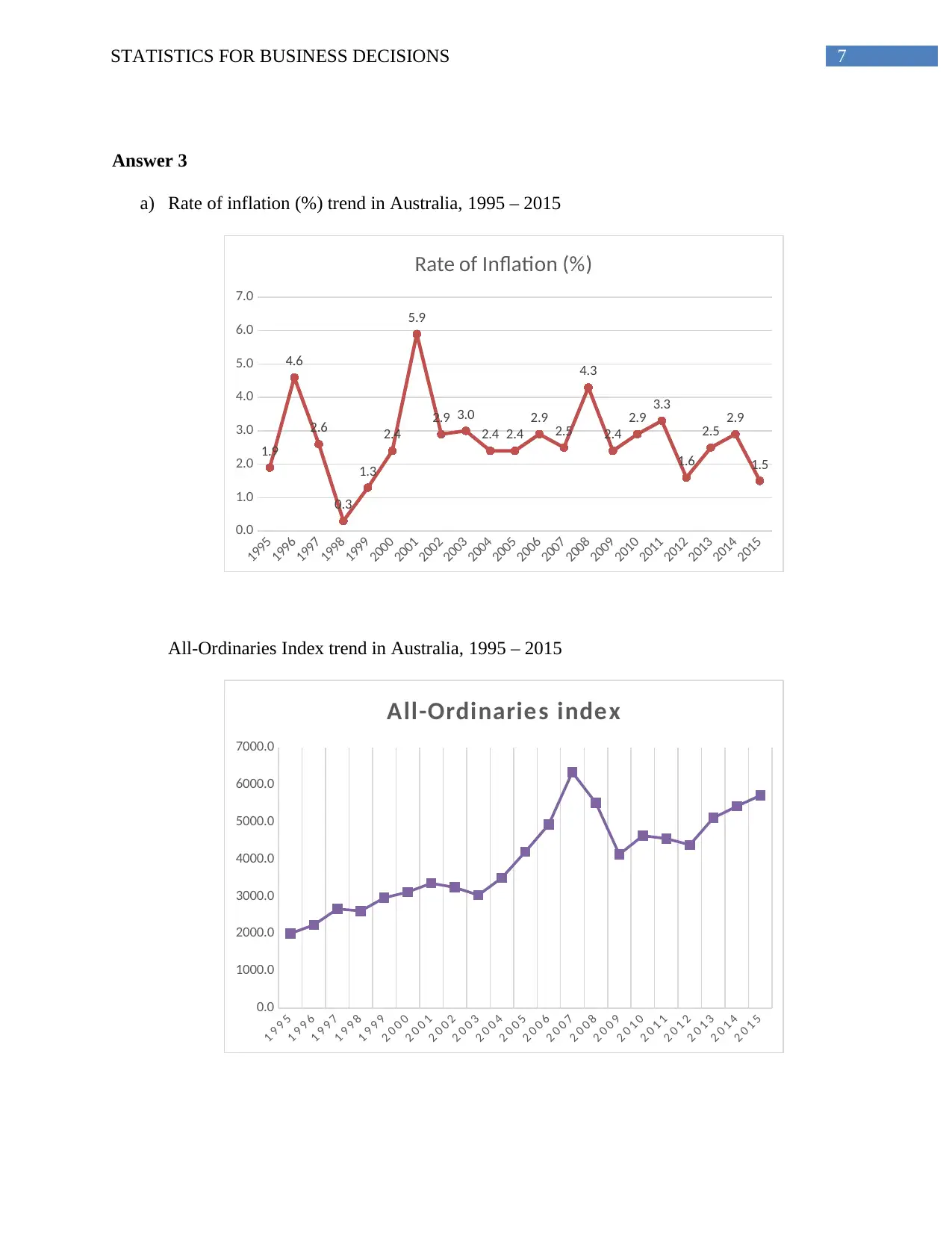
7STATISTICS FOR BUSINESS DECISIONS
Answer 3
a) Rate of inflation (%) trend in Australia, 1995 – 2015
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
1.9
4.6
2.6
0.3
1.3
2.4
5.9
2.9 3.0
2.4 2.4
2.9 2.5
4.3
2.4
2.9 3.3
1.6
2.5 2.9
1.5
Rate of Inflation (%)
All-Ordinaries Index trend in Australia, 1995 – 2015
1 9 9 5
1 9 9 6
1 9 9 7
1 9 9 8
1 9 9 9
2 0 0 0
2 0 0 1
2 0 0 2
2 0 0 3
2 0 0 4
2 0 0 5
2 0 0 6
2 0 0 7
2 0 0 8
2 0 0 9
2 0 1 0
2 0 1 1
2 0 1 2
2 0 1 3
2 0 1 4
2 0 1 5
0.0
1000.0
2000.0
3000.0
4000.0
5000.0
6000.0
7000.0
All-Ordinaries index

8STATISTICS FOR BUSINESS DECISIONS
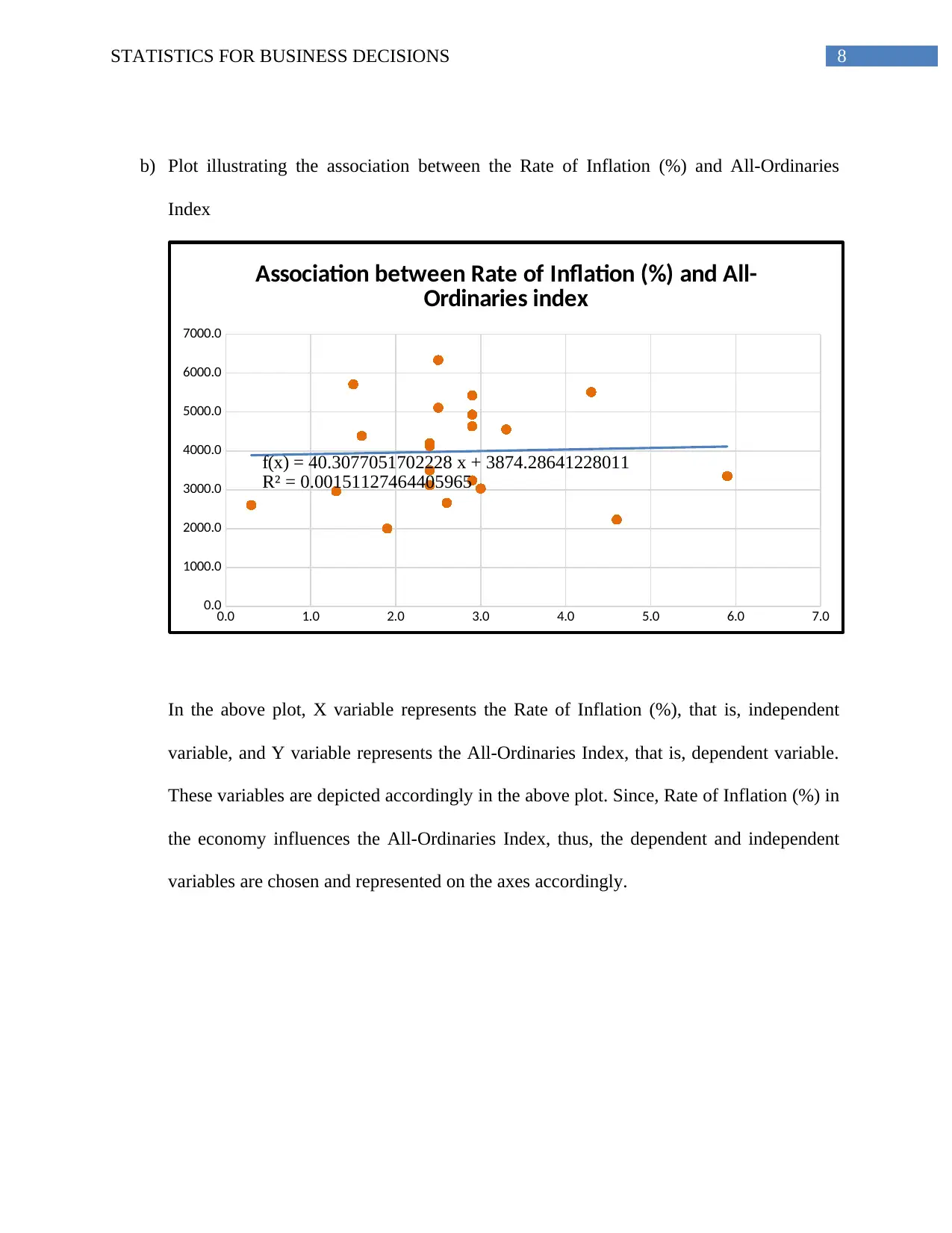
b) Plot illustrating the association between the Rate of Inflation (%) and All-Ordinaries
Index
0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0
0.0
1000.0
2000.0
3000.0
4000.0
5000.0
6000.0
7000.0
f(x) = 40.3077051702228 x + 3874.28641228011
R² = 0.00151127464405965
Association between Rate of Inflation (%) and All-
Ordinaries index
In the above plot, X variable represents the Rate of Inflation (%), that is, independent
variable, and Y variable represents the All-Ordinaries Index, that is, dependent variable.
These variables are depicted accordingly in the above plot. Since, Rate of Inflation (%) in
the economy influences the All-Ordinaries Index, thus, the dependent and independent
variables are chosen and represented on the axes accordingly.

9STATISTICS FOR BUSINESS DECISIONS
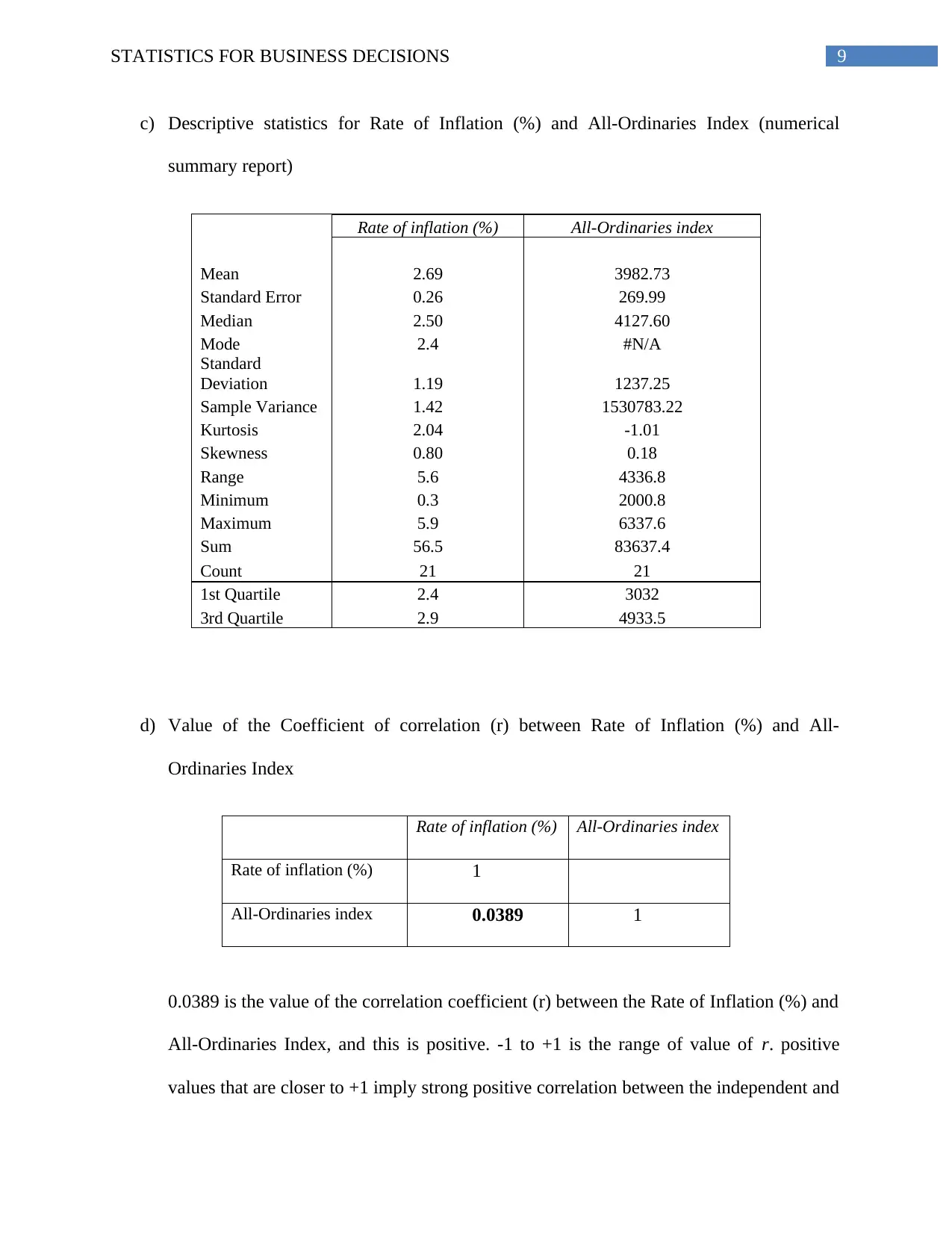
c) Descriptive statistics for Rate of Inflation (%) and All-Ordinaries Index (numerical
summary report)
Rate of inflation (%) All-Ordinaries index
Mean 2.69 3982.73
Standard Error 0.26 269.99
Median 2.50 4127.60
Mode 2.4 #N/A
Standard
Deviation 1.19 1237.25
Sample Variance 1.42 1530783.22
Kurtosis 2.04 -1.01
Skewness 0.80 0.18
Range 5.6 4336.8
Minimum 0.3 2000.8
Maximum 5.9 6337.6
Sum 56.5 83637.4
Count 21 21
1st Quartile 2.4 3032
3rd Quartile 2.9 4933.5
d) Value of the Coefficient of correlation (r) between Rate of Inflation (%) and All-
Ordinaries Index
Rate of inflation (%) All-Ordinaries index
Rate of inflation (%) 1
All-Ordinaries index 0.0389 1
0.0389 is the value of the correlation coefficient (r) between the Rate of Inflation (%) and
All-Ordinaries Index, and this is positive. -1 to +1 is the range of value of r. positive
values that are closer to +1 imply strong positive correlation between the independent and

10STATISTICS FOR BUSINESS DECISIONS
dependent variables, and negative values that are closer to -1 imply strong negative
correlation. Zero represents no correlation. Values, positive or negative, that are closer to
zero indicate an insignificant or negligible correlation between the variables (Zhou et al.
2016). In the given case, the correlation coefficient value is positive, however, much
closer to zero. Therefore, it indicates that the variables, that is, Rate of Inflation (%) and
All-Ordinaries Index are positively correlated, though, the magnitude of positive
correlation is not much impactful or strong.
e) Simple linear regression model equation:
Y =mX +C
In the given case, Y i.e. Dependent variable = All-Ordinaries Index
X, i.e., Independent variable = Rate of Inflation (%)
and, C = Constant
Regression hypothesis:
H0 (Null hypothesis): Rate of Inflation (%) does not have significant influence on All-
Ordinaries Index.
H1 (Alternate hypothesis): Rate of inflation (%) has significant influence on All-
Ordinaries Index.
Regression output:

11STATISTICS FOR BUSINESS DECISIONS
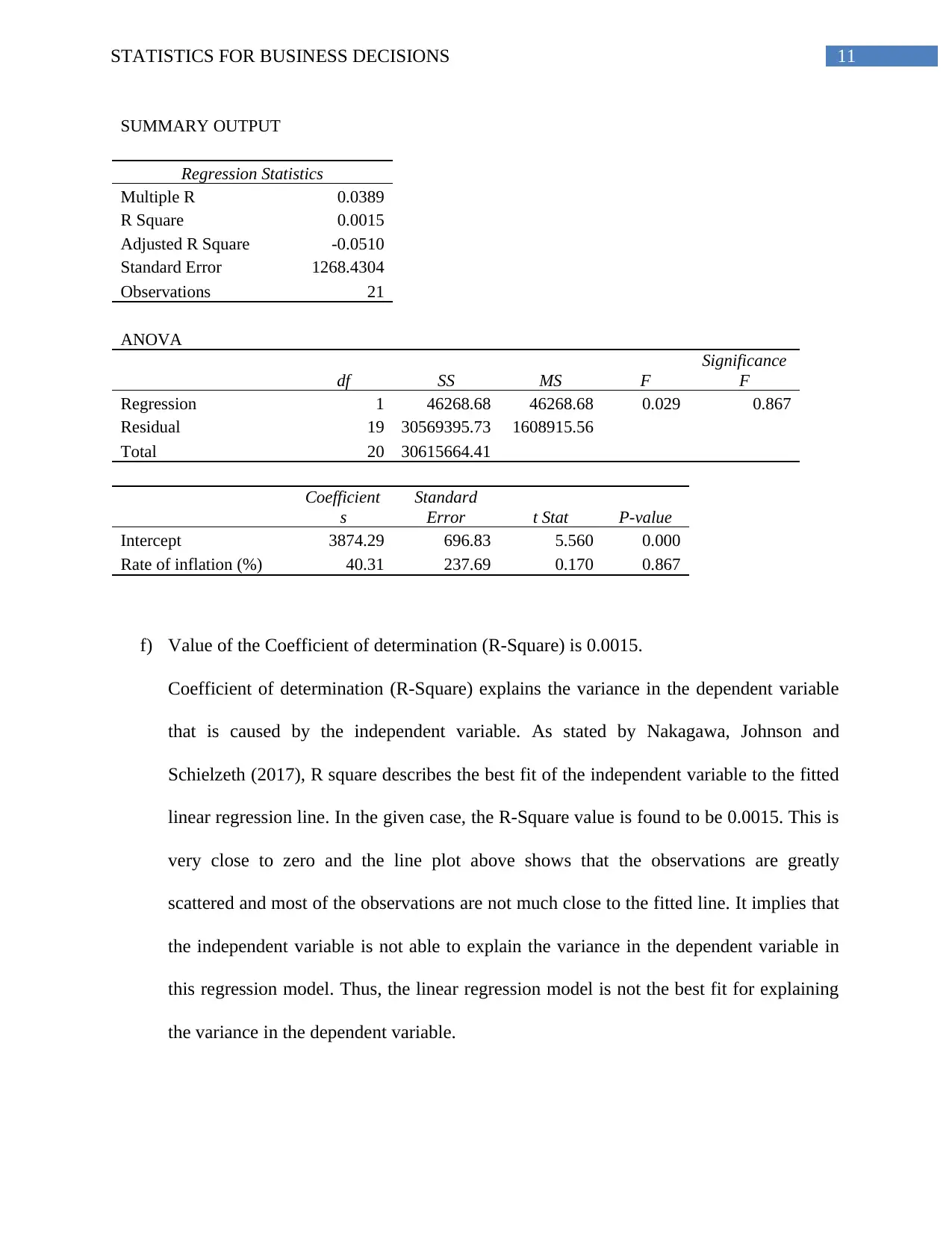
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.0389
R Square 0.0015
Adjusted R Square -0.0510
Standard Error 1268.4304
Observations 21
ANOVA
df SS MS F
Significance
F
Regression 1 46268.68 46268.68 0.029 0.867
Residual 19 30569395.73 1608915.56
Total 20 30615664.41
Coefficient
s
Standard
Error t Stat P-value
Intercept 3874.29 696.83 5.560 0.000
Rate of inflation (%) 40.31 237.69 0.170 0.867
f) Value of the Coefficient of determination (R-Square) is 0.0015.
Coefficient of determination (R-Square) explains the variance in the dependent variable
that is caused by the independent variable. As stated by Nakagawa, Johnson and
Schielzeth (2017), R square describes the best fit of the independent variable to the fitted
linear regression line. In the given case, the R-Square value is found to be 0.0015. This is
very close to zero and the line plot above shows that the observations are greatly
scattered and most of the observations are not much close to the fitted line. It implies that
the independent variable is not able to explain the variance in the dependent variable in
this regression model. Thus, the linear regression model is not the best fit for explaining
the variance in the dependent variable.