MATH221 Statistics for Decision Making - Week 4 Lab Assignment
VerifiedAdded on 2022/10/10
|6
|1229
|14
Homework Assignment
AI Summary
This assignment is a MATH221 Statistics for Decision Making Week 4 lab focusing on probability and the binomial probability distribution. The lab involves calculating descriptive statistics (mean and standard deviation) using a provided data file, and plotting binomial probabilities using Excel. Students are tasked with creating scatter plots for different probability values (p=0.50, p=0.10, and p=0.90) and calculating binomial probabilities. The assignment also includes hand calculations of the mean and standard deviation for binomial distributions, followed by comparisons of these statistics under different probability conditions. Students are required to analyze the coin variable and explain its representation of a binomial distribution based on the properties of a binomial experiment. The solution provides detailed calculations, plots, and comparative analysis to address all assignment questions.

1
MATH221 Statistics for Decision Making
Week 4 Lab
Name: _______________________
Statistical Concepts:
Probability
Binomial Probability Distribution
Calculating Binomial Probabilities
NOTE: For question 1, you will be using the same data file your instructor gave you
for the Week 2 lab.
1. Using the data file from your instructor (same one you used for the Week 2 lab),
calculate descriptive statistics for the variable (Coin) where each of the thirty-five
students in the sample flipped a coin 10 times. Round your answers to three decimal
places and type the mean and the standard deviation in the grey area below.
Mean:
4.571
Standard deviation:
1.929
NOTE: for questions 2-7, you will NOT be using the data file your instructor gave
you. Please follow the instructions given in each question.
Plotting the Binomial Probabilities
For the next part of the lab, open the Week 3 Excel worksheet. This will be used for
the next few questions, rather than the data file used for the first question.
1. Click on the “binomial tables” workbook
2. Type in n=10 and p=0.5; this simulates ten flips of a coin where x is counting the
number of heads that occur throughout the ten flips
3. Create a scatter plot, either directly in this spreadsheet (if you are comfortable
with those steps), or by using the week 1 spreadsheet and copying the data from
here onto that sheet (x would be the x variable, and P(X=x) would be the y
variable.
MATH221 Statistics for Decision Making
Week 4 Lab
Name: _______________________
Statistical Concepts:
Probability
Binomial Probability Distribution
Calculating Binomial Probabilities
NOTE: For question 1, you will be using the same data file your instructor gave you
for the Week 2 lab.
1. Using the data file from your instructor (same one you used for the Week 2 lab),
calculate descriptive statistics for the variable (Coin) where each of the thirty-five
students in the sample flipped a coin 10 times. Round your answers to three decimal
places and type the mean and the standard deviation in the grey area below.
Mean:
4.571
Standard deviation:
1.929
NOTE: for questions 2-7, you will NOT be using the data file your instructor gave
you. Please follow the instructions given in each question.
Plotting the Binomial Probabilities
For the next part of the lab, open the Week 3 Excel worksheet. This will be used for
the next few questions, rather than the data file used for the first question.
1. Click on the “binomial tables” workbook
2. Type in n=10 and p=0.5; this simulates ten flips of a coin where x is counting the
number of heads that occur throughout the ten flips
3. Create a scatter plot, either directly in this spreadsheet (if you are comfortable
with those steps), or by using the week 1 spreadsheet and copying the data from
here onto that sheet (x would be the x variable, and P(X=x) would be the y
variable.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
2
4. Repeat steps 2 and 3 with n=10 and p=0.10
5. Repeat steps 2 and 3 with n=10 and p=0.90
6. In the end, you will have three scatter plots for the first question below.
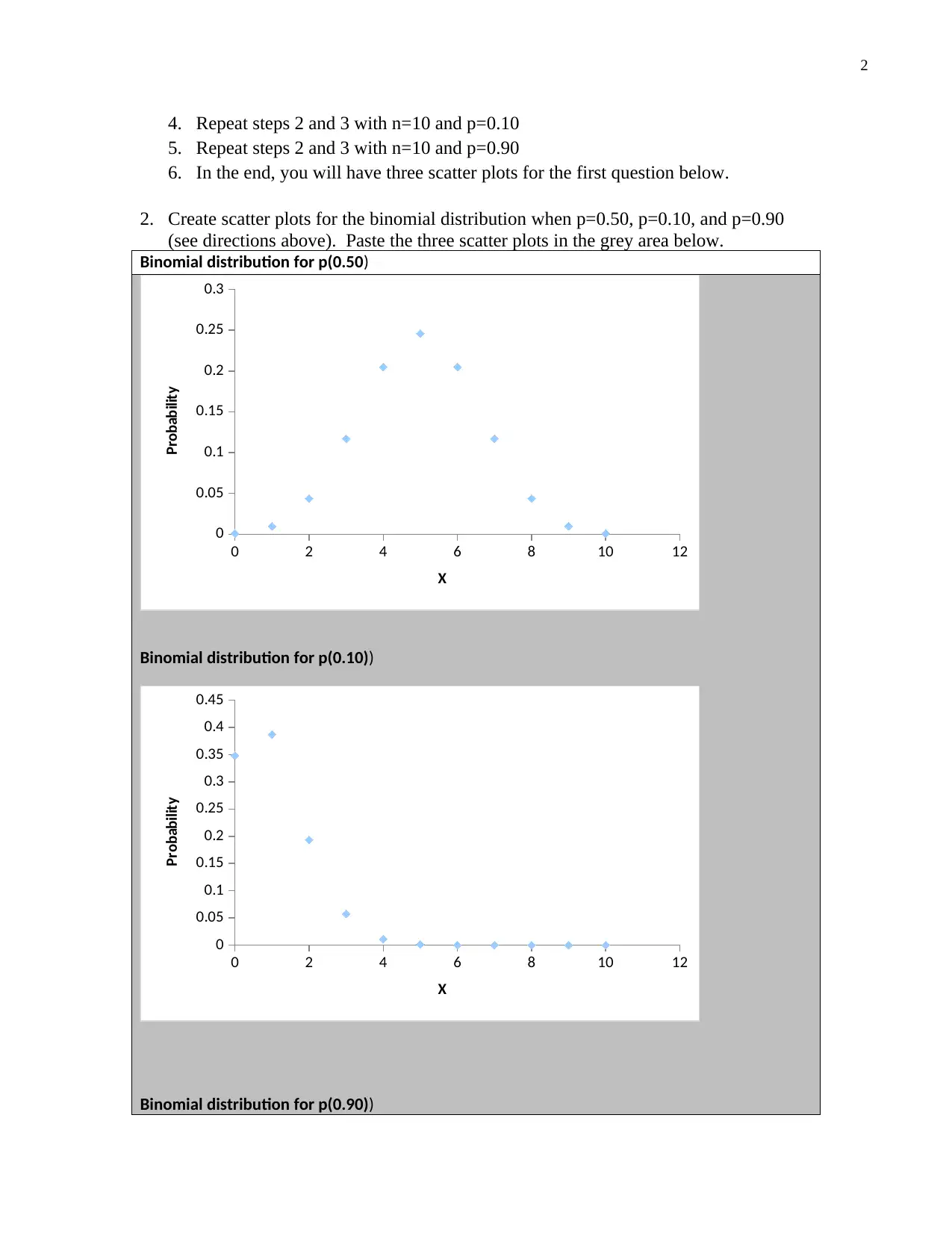
2. Create scatter plots for the binomial distribution when p=0.50, p=0.10, and p=0.90
(see directions above). Paste the three scatter plots in the grey area below.
Binomial distribution for p(0.50)
0 2 4 6 8 10 12
0
0.05
0.1
0.15
0.2
0.25
0.3
X
Probability
Binomial distribution for p(0.10))
0 2 4 6 8 10 12
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
X
Probability
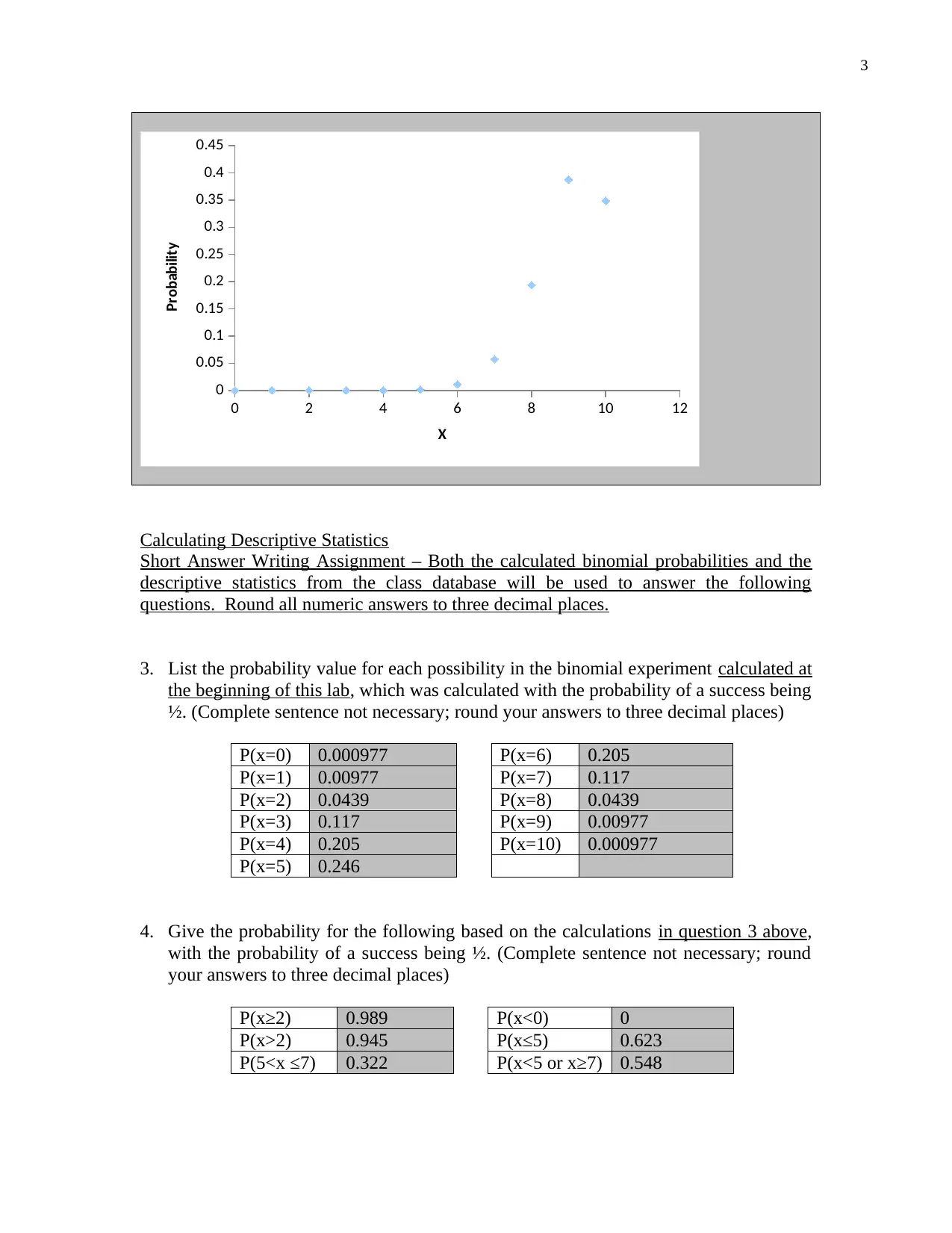
Binomial distribution for p(0.90))
4. Repeat steps 2 and 3 with n=10 and p=0.10
5. Repeat steps 2 and 3 with n=10 and p=0.90
6. In the end, you will have three scatter plots for the first question below.
2. Create scatter plots for the binomial distribution when p=0.50, p=0.10, and p=0.90
(see directions above). Paste the three scatter plots in the grey area below.
Binomial distribution for p(0.50)
0 2 4 6 8 10 12
0
0.05
0.1
0.15
0.2
0.25
0.3
X
Probability
Binomial distribution for p(0.10))
0 2 4 6 8 10 12
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
X
Probability
Binomial distribution for p(0.90))
3
0 2 4 6 8 10 12
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
X
Probability
Calculating Descriptive Statistics
Short Answer Writing Assignment – Both the calculated binomial probabilities and the
descriptive statistics from the class database will be used to answer the following
questions. Round all numeric answers to three decimal places.
3. List the probability value for each possibility in the binomial experiment calculated at
the beginning of this lab, which was calculated with the probability of a success being
½. (Complete sentence not necessary; round your answers to three decimal places)
P(x=0) 0.000977 P(x=6) 0.205
P(x=1) 0.00977 P(x=7) 0.117
P(x=2) 0.0439 P(x=8) 0.0439
P(x=3) 0.117 P(x=9) 0.00977
P(x=4) 0.205 P(x=10) 0.000977
P(x=5) 0.246
4. Give the probability for the following based on the calculations in question 3 above,
with the probability of a success being ½. (Complete sentence not necessary; round
your answers to three decimal places)
P(x≥2) 0.989 P(x<0) 0
P(x>2) 0.945 P(x≤5) 0.623
P(5<x ≤7) 0.322 P(x<5 or x≥7) 0.548
0 2 4 6 8 10 12
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
X
Probability
Calculating Descriptive Statistics
Short Answer Writing Assignment – Both the calculated binomial probabilities and the
descriptive statistics from the class database will be used to answer the following
questions. Round all numeric answers to three decimal places.
3. List the probability value for each possibility in the binomial experiment calculated at
the beginning of this lab, which was calculated with the probability of a success being
½. (Complete sentence not necessary; round your answers to three decimal places)
P(x=0) 0.000977 P(x=6) 0.205
P(x=1) 0.00977 P(x=7) 0.117
P(x=2) 0.0439 P(x=8) 0.0439
P(x=3) 0.117 P(x=9) 0.00977
P(x=4) 0.205 P(x=10) 0.000977
P(x=5) 0.246
4. Give the probability for the following based on the calculations in question 3 above,
with the probability of a success being ½. (Complete sentence not necessary; round
your answers to three decimal places)
P(x≥2) 0.989 P(x<0) 0
P(x>2) 0.945 P(x≤5) 0.623
P(5<x ≤7) 0.322 P(x<5 or x≥7) 0.548
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

4
5. Calculate (by hand) the mean and standard deviation for the binomial distribution
with the probability of a success being 0.50 and n = 10. Either show work or explain
how your answer was calculated. Use these formulas to do the hand calculations:
Mean = np, Standard Deviation =
Mean = np:
=10*0.50
=5
Standard Deviation = : where q = 0.5
= √10*0.5*0.5
=√2.5
=1.581
6. Calculate (by hand) the mean and standard deviation for the binomial distribution
with the probability of a success being 0.10 and n = 10. Write a comparison of these
statistics to those from question 5 in a short paragraph of several complete sentences.
Use these formulas to do the hand calculations: Mean = np, Standard Deviation =
Mean = np:
=10*0.10
=1
Standard Deviation = : where q= 0.90
=√10*0.10*0.90
=√0.9
= 0.949
Comparison:
In question 5 above, both the mean and standard deviation for the binomial distribution
with probability of success (0.50) are greater than the mean and standard deviation for the
binomial distribution with probability of success (0.10).
7. Calculate (by hand) the mean and standard deviation for the binomial distribution
with the probability of a success being 0.90 and n = 10. Write a comparison of these
statistics to those from question 6 in a short paragraph of several complete sentences.
Use these formulas to do the hand calculations: Mean = np, Standard Deviation =
npq
npq
npq
npq
npq
5. Calculate (by hand) the mean and standard deviation for the binomial distribution
with the probability of a success being 0.50 and n = 10. Either show work or explain
how your answer was calculated. Use these formulas to do the hand calculations:
Mean = np, Standard Deviation =
Mean = np:
=10*0.50
=5
Standard Deviation = : where q = 0.5
= √10*0.5*0.5
=√2.5
=1.581
6. Calculate (by hand) the mean and standard deviation for the binomial distribution
with the probability of a success being 0.10 and n = 10. Write a comparison of these
statistics to those from question 5 in a short paragraph of several complete sentences.
Use these formulas to do the hand calculations: Mean = np, Standard Deviation =
Mean = np:
=10*0.10
=1
Standard Deviation = : where q= 0.90
=√10*0.10*0.90
=√0.9
= 0.949
Comparison:
In question 5 above, both the mean and standard deviation for the binomial distribution
with probability of success (0.50) are greater than the mean and standard deviation for the
binomial distribution with probability of success (0.10).
7. Calculate (by hand) the mean and standard deviation for the binomial distribution
with the probability of a success being 0.90 and n = 10. Write a comparison of these
statistics to those from question 6 in a short paragraph of several complete sentences.
Use these formulas to do the hand calculations: Mean = np, Standard Deviation =
npq
npq
npq
npq
npq
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

5
Mean = np:
= 10*0.9
=9
Standard Deviation = : where q = 0.10
= √10*0.90*0.10
= √0.9
= 0.949
Comparison:
In question 6 above the mean for the binomial distribution with probability of success of
0.1 has a smaller mean compared to the mean for the binomial distribution with
probability of success of 0.9.
However both the questions that is question 6 and 7 share a common standard deviation
of 0.949.
NOTE: For questions 8-9, you will use the results of the previous questions.
8. Using all four of the properties of a Binomial experiment (see page 201 in the
textbook) explain in a short paragraph of several complete sentences why the Coin
variable from the class survey represents a binomial distribution from a binomial
experiment.
The coin variable from the class survey represents a binomial distribution from a
binomial experiment because of the following;
i. The experiment consist of n=10repeated trials.
ii. Each trial can only result to two possible outcomes that is head or tail.
iii. The probability of success (p) is equal on every trial.
iv. And last but not least the trial n=10 are independent that is the outcome of one
trial doesn’t have an effect on the outcome of the other.
9. Compare the mean and standard deviation for the Coin variable (question 1) with
those of the mean and standard deviation for the binomial distribution that was
calculated by hand in question 5. Explain how they are related in a short paragraph of
several complete sentences.
Mean from question #1: 4.571
Standard deviation from question #1:
1.929
Mean from question #5:
5
npq
Mean = np:
= 10*0.9
=9
Standard Deviation = : where q = 0.10
= √10*0.90*0.10
= √0.9
= 0.949
Comparison:
In question 6 above the mean for the binomial distribution with probability of success of
0.1 has a smaller mean compared to the mean for the binomial distribution with
probability of success of 0.9.
However both the questions that is question 6 and 7 share a common standard deviation
of 0.949.
NOTE: For questions 8-9, you will use the results of the previous questions.
8. Using all four of the properties of a Binomial experiment (see page 201 in the
textbook) explain in a short paragraph of several complete sentences why the Coin
variable from the class survey represents a binomial distribution from a binomial
experiment.
The coin variable from the class survey represents a binomial distribution from a
binomial experiment because of the following;
i. The experiment consist of n=10repeated trials.
ii. Each trial can only result to two possible outcomes that is head or tail.
iii. The probability of success (p) is equal on every trial.
iv. And last but not least the trial n=10 are independent that is the outcome of one
trial doesn’t have an effect on the outcome of the other.
9. Compare the mean and standard deviation for the Coin variable (question 1) with
those of the mean and standard deviation for the binomial distribution that was
calculated by hand in question 5. Explain how they are related in a short paragraph of
several complete sentences.
Mean from question #1: 4.571
Standard deviation from question #1:
1.929
Mean from question #5:
5
npq

6
Standard deviation from question #5:
1.581
Comparison and explanation:
Question 5 above has a higher mean of 5 compared to that of question 1 which is 4.571.
Moreover the standard deviation (1.929) for question 1 is higher than that of question 5
which is 1.581.
The difference in mean and standard deviation for both questions arises because of the
different of the number of successes (p) in the questions.
Standard deviation from question #5:
1.581
Comparison and explanation:
Question 5 above has a higher mean of 5 compared to that of question 1 which is 4.571.
Moreover the standard deviation (1.929) for question 1 is higher than that of question 5
which is 1.581.
The difference in mean and standard deviation for both questions arises because of the
different of the number of successes (p) in the questions.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 6
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

