N7010 Statistics Midterm Exam Problems and Solutions, Summer 2024

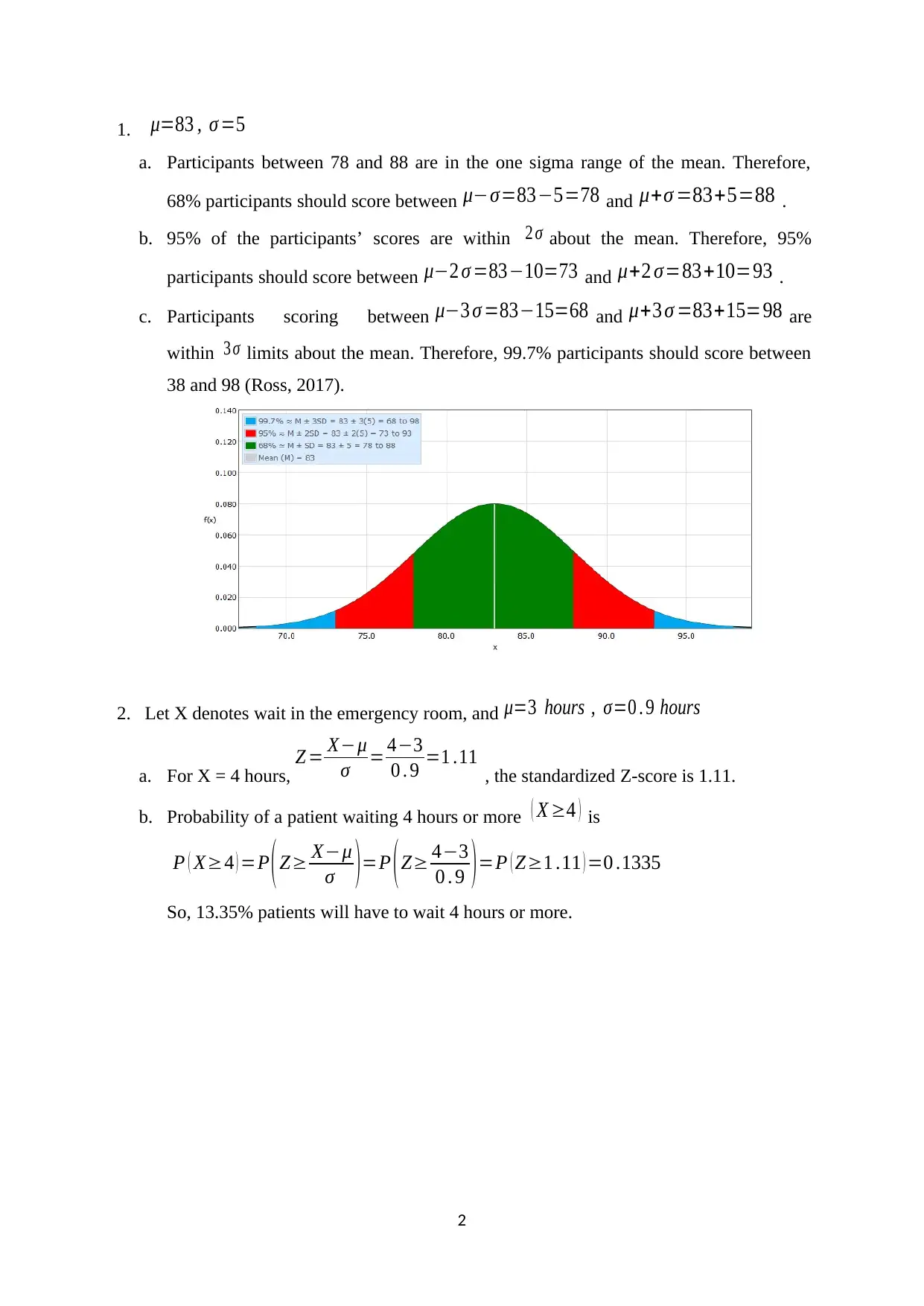
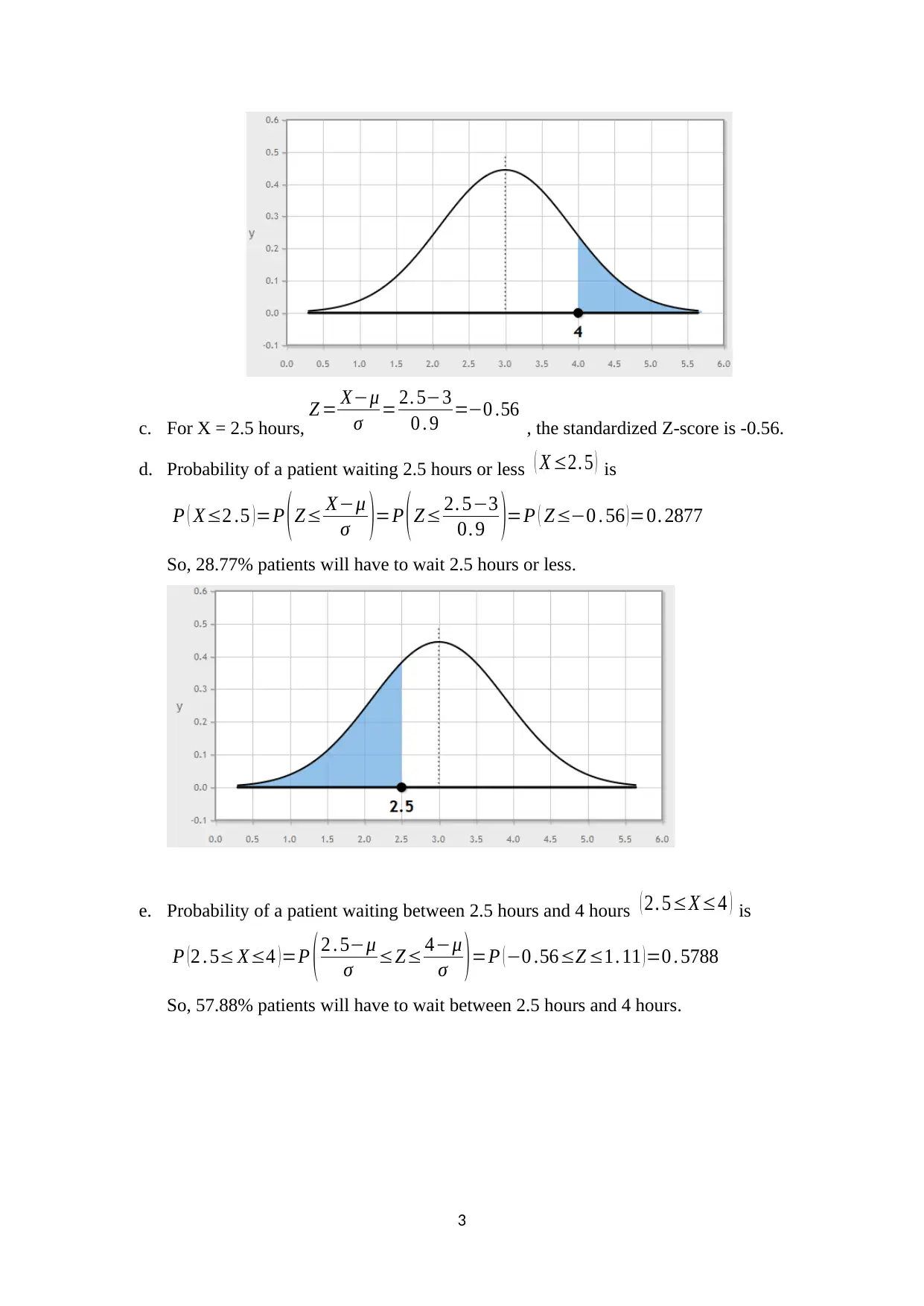
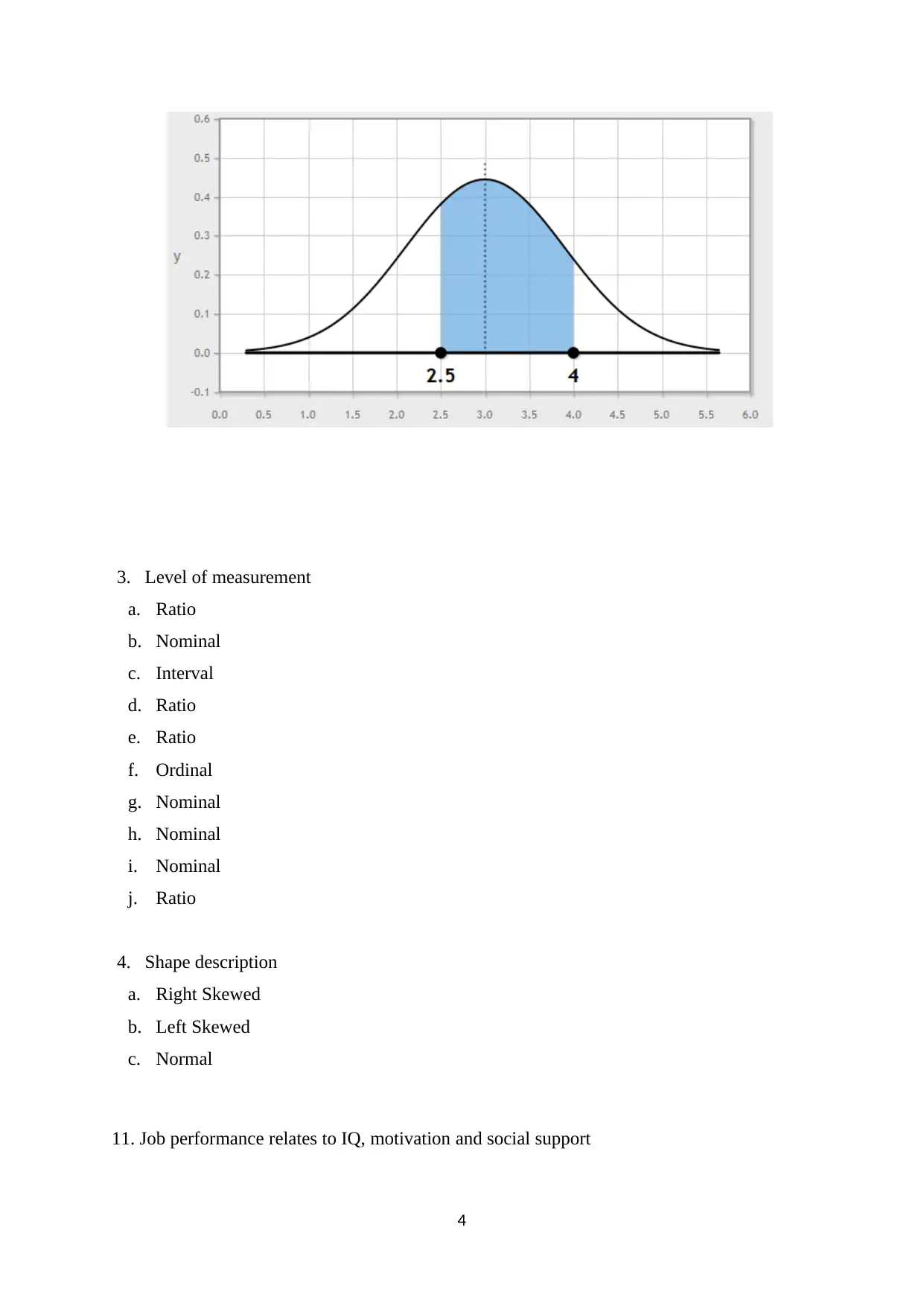
This document presents solutions to a statistics midterm exam, covering key concepts such as the normal distribution, Z-scores, and their application in analyzing data. The solutions include calculations for the one-sigma range, and the probabilities associated with different wait times in an emergency room. Furthermore, the document addresses questions related to job performance, including the correlation between IQ, motivation, and social support, interpreting p-values, and the coefficient of determination. The analysis includes the identification of the level of measurement for various variables and the interpretation of statistical measures like the t-statistic and median, providing a comprehensive overview of statistical analysis and interpretation.

Midterm Exam Problems on Statistics
1

1. μ=83 , σ =5
a. Participants between 78 and 88 are in the one sigma range of the mean. Therefore,
68% participants should score between μ−σ=83−5=78 and μ+σ =83+5=88 .
b. 95% of the participants’ scores are within 2 σ about the mean. Therefore, 95%
participants should score between μ−2 σ =83−10=73 and μ+2 σ=83+10=93 .
c. Participants scoring between μ−3 σ =83−15=68 and μ+3 σ =83+15=98 are
within 3 σ limits about the mean. Therefore, 99.7% participants should score between
38 and 98 (Ross, 2017).
2. Let X denotes wait in the emergency room, and μ=3 hours , σ=0 . 9 hours
a. For X = 4 hours,
Z = X−μ
σ = 4−3
0 . 9 =1 .11 , the standardized Z-score is 1.11.
b. Probability of a patient waiting 4 hours or more ( X ≥4 ) is
P ( X≥4 ) =P ( Z≥ X−μ
σ ) =P ( Z≥ 4−3
0 . 9 ) =P ( Z≥1 .11 ) =0 .1335
So, 13.35% patients will have to wait 4 hours or more.
2

c. For X = 2.5 hours,
Z = X−μ
σ = 2. 5−3
0 . 9 =−0 .56 , the standardized Z-score is -0.56.
d. Probability of a patient waiting 2.5 hours or less ( X ≤2. 5 ) is
P ( X≤2 .5 ) =P ( Z≤ X−μ
σ )=P ( Z≤ 2. 5−3
0. 9 )=P ( Z≤−0 . 56 ) =0. 2877
So, 28.77% patients will have to wait 2.5 hours or less.
e. Probability of a patient waiting between 2.5 hours and 4 hours ( 2. 5≤X≤4 ) is
P ( 2 . 5≤ X≤4 ) =P ( 2 . 5−μ
σ ≤Z≤ 4−μ
σ ) =P ( −0 .56≤Z ≤1. 11 ) =0 . 5788
So, 57.88% patients will have to wait between 2.5 hours and 4 hours.
3

3. Level of measurement
a. Ratio
b. Nominal
c. Interval
d. Ratio
e. Ratio
f. Ordinal
g. Nominal
h. Nominal
i. Nominal
j. Ratio
4. Shape description
a. Right Skewed
b. Left Skewed
c. Normal
11. Job performance relates to IQ, motivation and social support
4

a. Mean = 78.12, Standard deviation = 8.03
b. Correlation between Outcome of IQ test and Outcome of social support test is -0.09. There
was no evidence of statistical significance (p = 0.49) for the correlation between Outcome of
IQ test and Outcome of social support test.
c. The p-value < 0.01 corresponding to the correlation between outcome of job
performance test and outcome of job motivation test.
d. The coefficient of determination is 0.654.
e. Yes, all the variables are significant in the model since p-value for all the variables are less
than 0.01.
f. Outcome of job motivation test has the greatest impact ( B=0 . 31, t=6 . 16 , p< 0 .01 ) on the
outcome of job performance test.
12. The data sample is not normally distributed.
13. Variances in different groups are approximately equal
14. A measure of the strength of relationship between two variables
15. The t-statistic provides some idea of how well a predictor predicts the outcome variable.
16. The median
References
Ross, A. (2017). Area Under the Normal Curve. In Pedagogy and Content in Middle and
High School Mathematics (pp. 131-140). Brill Sense.
5