Statistics Assignment - Analysis of Financial Data and Probability

This document presents a complete solution to a statistics assignment, addressing various statistical concepts and techniques. The assignment covers topics such as stem and leaf plots, probability calculations, data analysis, and confidence intervals. The solution includes calculations for open prices of NAB and WBC stocks, analysis of total assets, and probability assessments related to internet access in households. It also involves calculations of means, standard deviations, and confidence intervals, along with interpretations of the results. The assignment provides a detailed breakdown of each question, offering step-by-step solutions and explanations to help students understand the statistical principles involved.

Question 1
Open prices for NAB and WBC from 2009 to 2017
Year Quarter NAB WBC
2009 1 19.85 15.66
2009 2 19.14 12.27
2009 3 21.02 18.03
2009 4 29.11 21.26
2010 1 25.97 25.8
2010 2 26.07 30.05
2010 3 21.9 31.35
2010 4 24.29 42.27
2011 1 22.55 61.38
2011 2 24.57 62
2011 3 24.31 69.41
2011 4 20.8 37.52
2012 1 22.22 44.81
2012 2 23.54 60.36
2012 3 22.55 53.14
2012 4 24.26 57.77
2013 1 23.78 66.18
2013 2 29.34 70.64
2013 3 27.95 75.08
2013 4 32.72 84.5
2014 1 33.13 93.11
2014 2 33.72 106.28
2014 3 31.21 107.29
2014 4 30.57 90.5
2015 1 31.96 105.91
2015 2 36.55 122.88
2015 3 32.28 124.8
2015 4 28.98 113.71
2016 1 29.14 100.24
2016 2 25.9 104.76
2016 3 25.63 91.6
2016 4 28 113.43
2017 1 30.67 106.96
2017 2 33.17 117.45
2017 3 29.61 129.19
2017 4 31.54 156.08

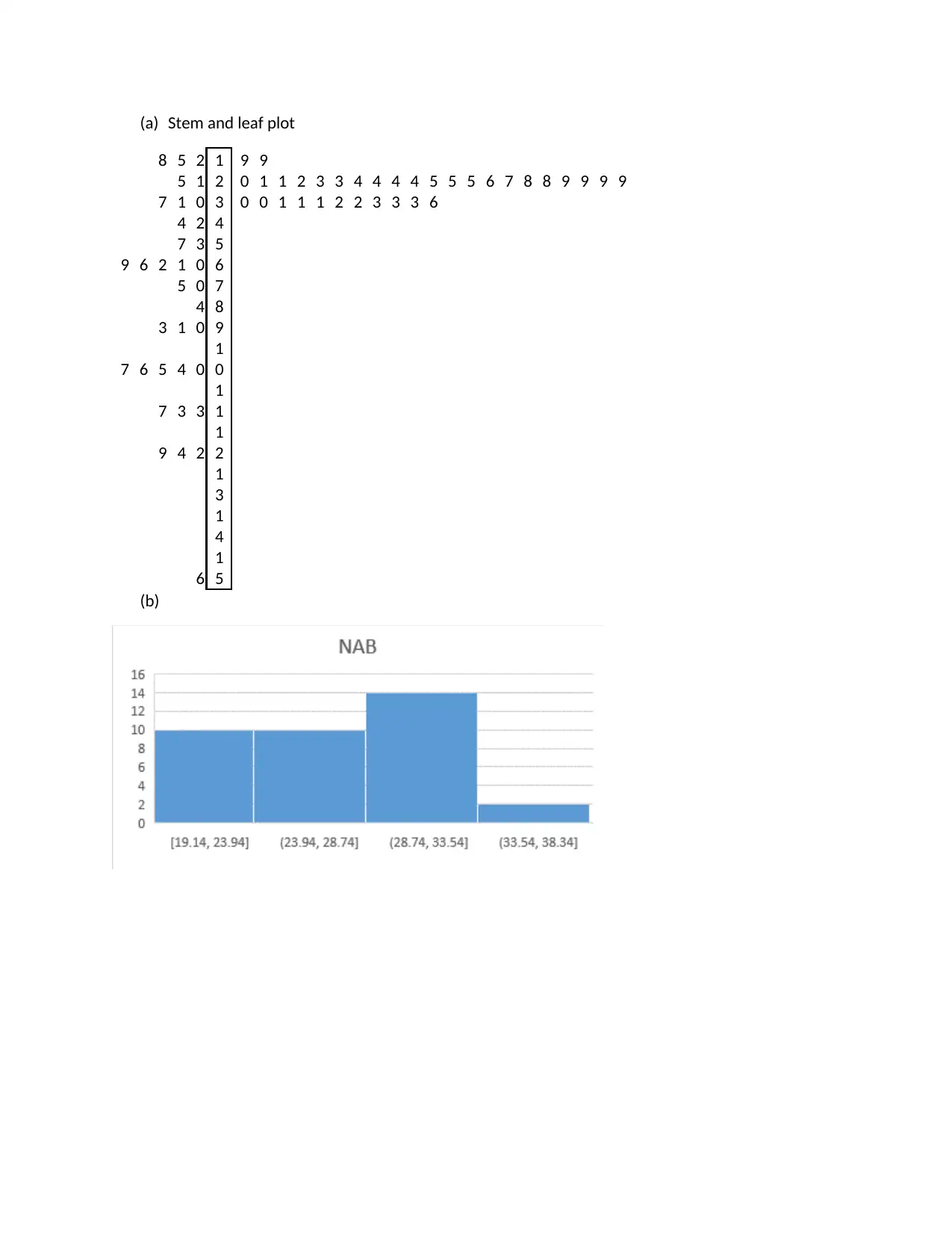
(a) Stem and leaf plot
8 5 2 1 9 9
5 1 2 0 1 1 2 3 3 4 4 4 4 5 5 5 6 7 8 8 9 9 9 9
7 1 0 3 0 0 1 1 1 2 2 3 3 3 6
4 2 4
7 3 5
9 6 2 1 0 6
5 0 7
4 8
3 1 0 9
7 6 5 4 0
1
0
7 3 3
1
1
9 4 2
1
2
1
3
1
4
6
1
5
(b)

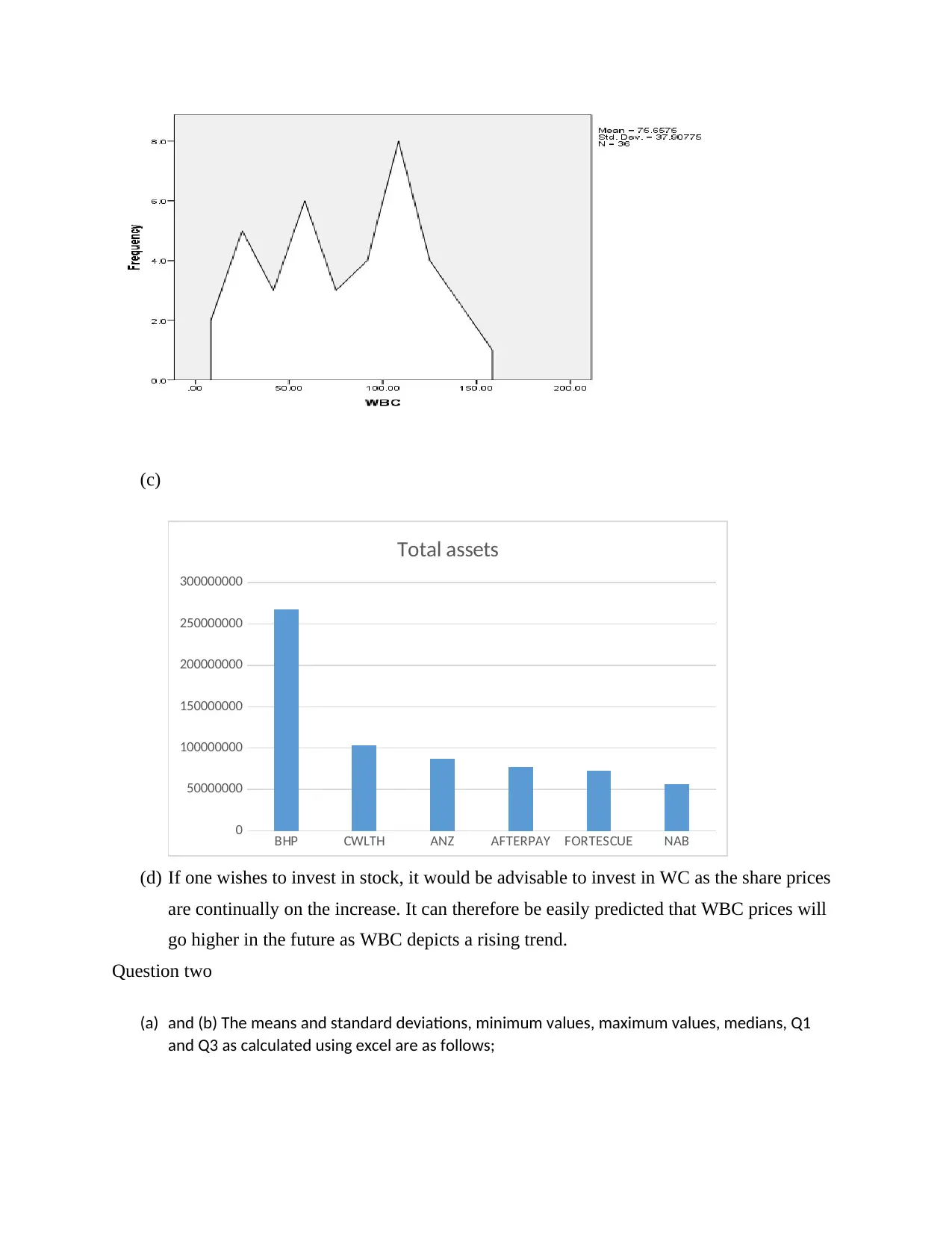
(c)
BHP CWLTH ANZ AFTERPAY FORTESCUE NAB
0
50000000
100000000
150000000
200000000
250000000
300000000
Total assets
(d) If one wishes to invest in stock, it would be advisable to invest in WC as the share prices
are continually on the increase. It can therefore be easily predicted that WBC prices will
go higher in the future as WBC depicts a rising trend.
Question two
(a) and (b) The means and standard deviations, minimum values, maximum values, medians, Q1
and Q3 as calculated using excel are as follows;

(C)
d.
Sales in the state of NSW are the highest, followed by sales in the state of VIC, followed by
QLD, followed by WA, followed by SA, followed by TAS, followed by ACT and the least sales
of new cars is in the state of NT.
Question three
a) The total number of houses that have internet access between 2008 to 2017 is 35466.1.
The total number of houses with internet access between 2008 to 2017 in Victoria is
8925.1.
Therefore, the probability of randomly selecting a household that lives in Victoria is;
8925.1
35466.1=0.2517
NSW VIC QLD SA WA TAS NT ACT
Jan-16 28392 22426 17193 5208 7861 1298 626 1509
Feb-16 32633 26782 18711 5988 8725 1319 851 1528
Mar-16 35963 27716 21470 6087 9054 1515 1023 1550
Apr-16 29391 23963 17753 5174 7601 1313 969 1563
May-16 32867 26125 19565 5949 7935 1503 1180 1560
Jun-16 43449 34262 27270 7613 10749 1853 1240 1542
Jul-16 30219 25517 18445 5210 8234 1389 831 1524
Aug-16 31788 27096 18062 5785 8144 1743 881 1519
Sep-16 34424 28766 19702 6551 8668 2074 880 1531
Oct-16 31850 27546 16870 5450 7580 1937 713 1552
Nov-16 32955 28991 18733 6259 7657 1903 808 1570
Dec-16 33632 27065 19252 6464 8026 1918 734 1573
Mean
33130.2
5
27187.9
2
19418.8
3
5978.16
7 8352.833
1647.08
3
894.666
7
1543.41
7
Std
3874.42
6
2913.56
1
2762.80
7
705.478
9 889.2711
286.471
1
182.790
7
21.1249
9
minimum 28392 22426 16870 5174 7580 1298 626 1509
maximu
m 43449 34262 27270 7613 10749 2074 1240 1573
median 32750 27080.5 18722 5968.5 8085 1629 865.5 1546
Q1
31395.7
5 25973
17984.7
5 5390 7810 1371.5 789.5 1527
Q3 33830 27978.5
19599.2
5 6310.25 8682.25 1906.75 982.5 1560.75

b) The total number of households with internet access in Tasmania between 2008 and 2017
is 786.2. Given this, the probability of randomly selecting a household that lives in
Tasmania is 786.2
35466.1=0.0222.
The total number of households that had internet access between 2010-2011 is 6723.6.
The probability that a household had internet access in Tasmania in 2010-11 is;
146.2
6723.6 =0.0217
Therefore, the probability that a randomly selected household lives in Tasmania and has
an internet access in the year 2010-11 is;
0.0222∗0.0217=0.00048174.
c) The total number of households with internet access in 2012-13 was 7343.2.
The probability that a household had internet access in 2012-13 is;
7343.2
35466.1=0.2070
The probability that a household is selected from New South Wales is;
2274.5
7343.2 =0.3097
The probability that a randomly selected household lives in New South Wales given a
household has internet access in 2012-13 is;
0.2070∗0.3097
0.2070 =0.3097
d) The probability that a household has internet access in 2010-11 is 6723.6
35466.1=0.1896
The probability that a household has internet access in 2012-13 is 7343.2
35466.1=0.2070
The probability that a household had internet access in 2010-11 and 2012-13 is;

0.1896∗0.2070=0.0392.
The probability of selecting a house in 2010-11 or 2012-13 is;
0.1896+0.2070−0.0392=0.3574
Question four
a) The upper 5% exceeds a value of 0.05*73=3.65 minutes.
b) The probability that temperature will be below 21 degrees Celsius is 9
14 =0.6429
c) (i) P=0.5 ,n=200
Pr (X >65)= √[0.65(1−0.65)/200]
¿ 0.0337
(ii) Pr ( X >50)= √ [(0.25 /200)]=0.0354
Pr (50< X <65)=Pr ( X <65)−Pr (X >50)
¿(1−0.0337)−0.0354=0.9309
Question five
a) Pr(280<X<355)
P=0.70
Pr(X>280)=Pr(p>0.56)
0.56*0.70=0.392
Pr(X<355)=Pr(p<0.71)
=0.29*0.7=0.0203
Pr(0.56<p<0.71)=0.392-0.0203=0.37117
b) P= 210
500 =0.42

Z ( p<0.50 ) = ( 0.50−0.42 )
√ ( 0.42 ( 1−0.42 )
500 ) = 0.08
√ ( 0.0004872 ) = 0.08
0.0221 =3.62
P(Z<3.62)=0.99985
c) X_bar=101.22, s.d=21.88
Upper limit= 101.22+ 1.96∗21.88
3 =101.51
Lower limit=101.22− 1.96∗21.88
3 =86.93
Therefore, the 95% confidence interval is;
86.93<μ<101.51