Statistics for Analytical Decisions: Statistical Analysis Homework
VerifiedAdded on 2021/05/31
|7
|1045
|35
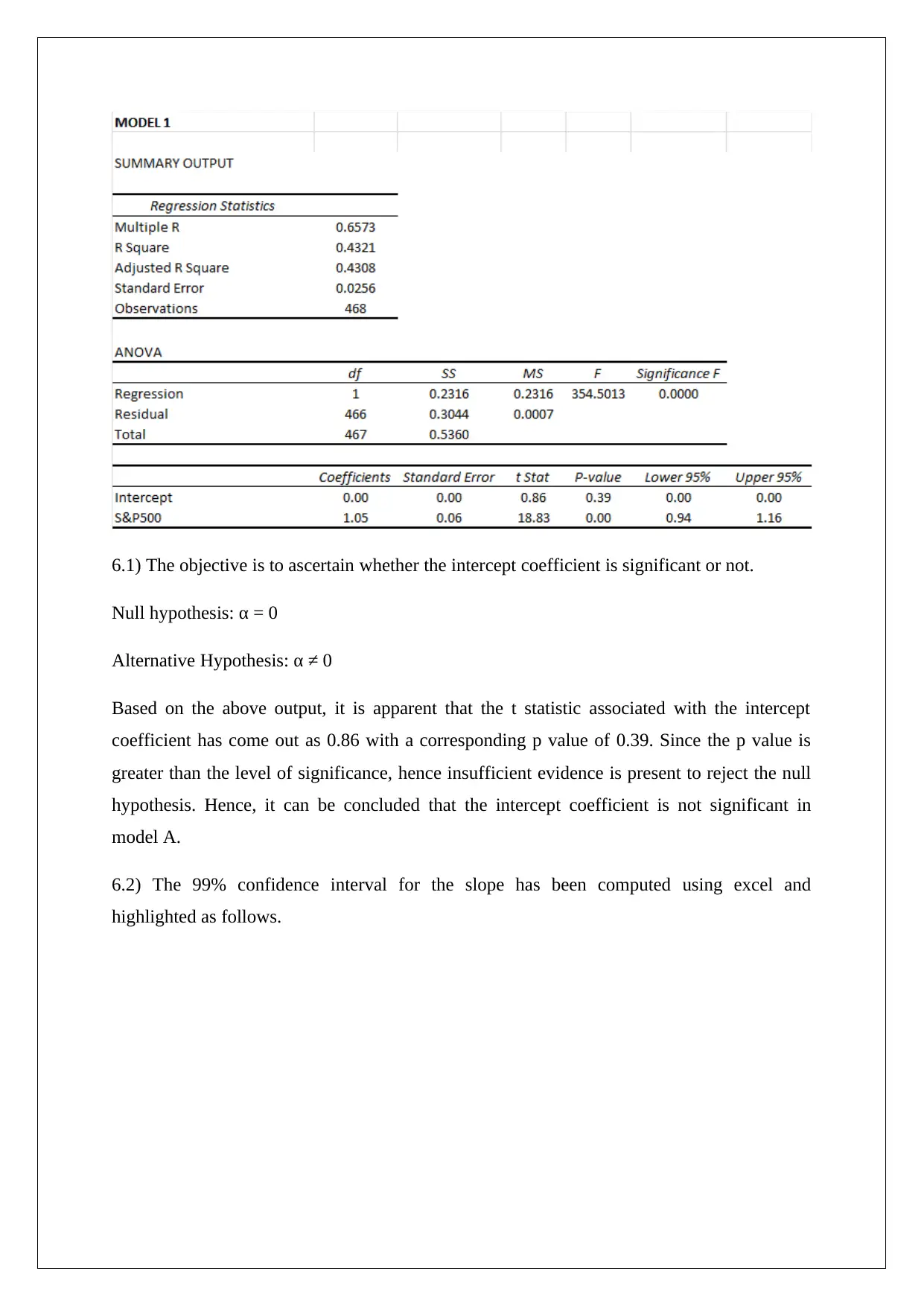
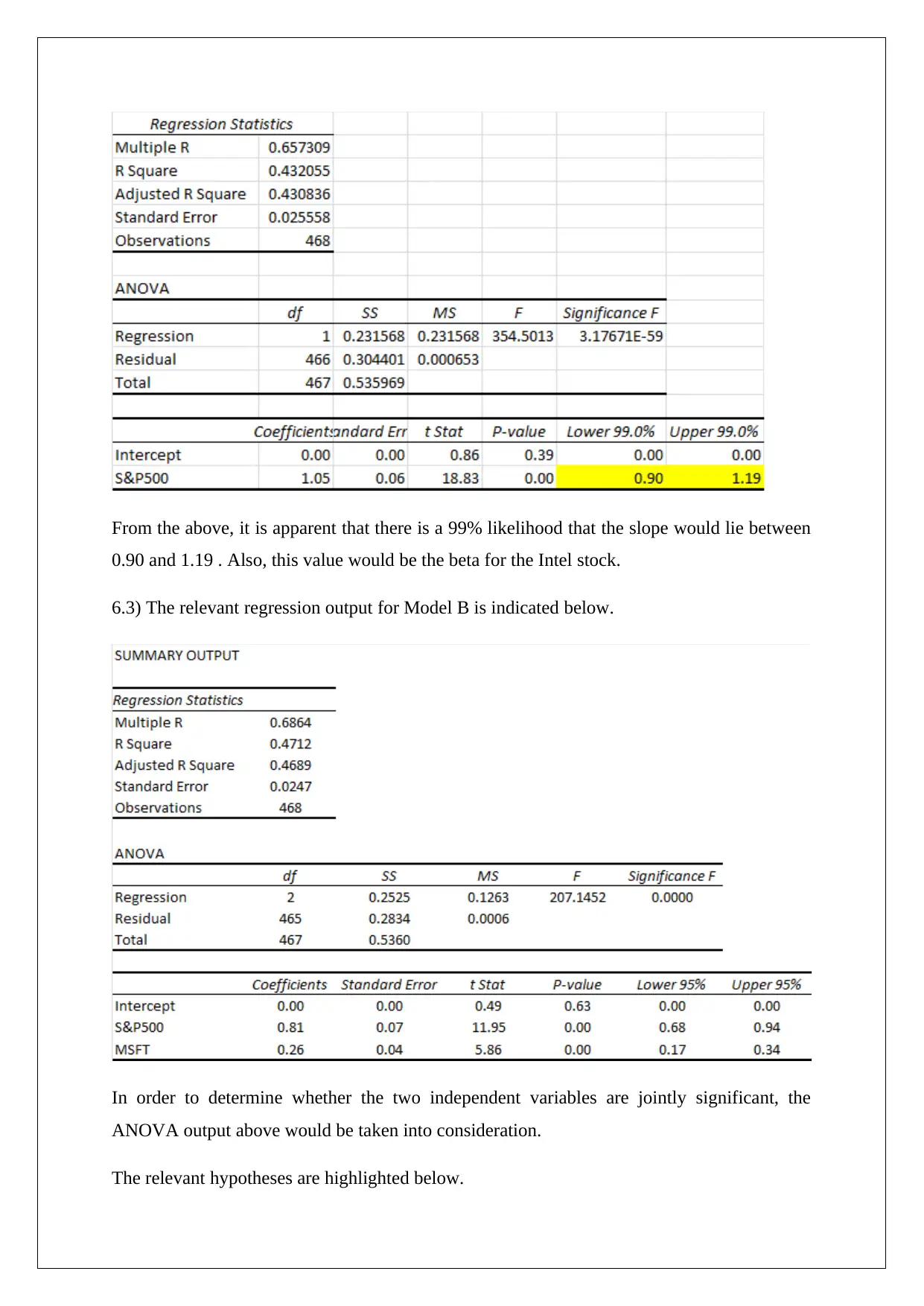
Homework Assignment
AI Summary
This document presents a complete solution to a statistics assignment focused on analytical decision-making. The assignment covers several key statistical concepts, including calculating weekly returns, assessing relative risk using standard deviation, and determining probabilities. It involves hypothesis testing on NASDAQ and S&P 500 returns, utilizing t-tests and p-values to draw conclusions. Furthermore, the solution explores covariance and correlation coefficients between stock returns. Regression analysis is performed using two models (A and B), evaluating the significance of intercept and slope coefficients, constructing confidence intervals, and comparing model performance based on R-squared values and ANOVA outputs. The analysis aims to determine the best model for predicting stock returns and assessing the joint significance of independent variables. This resource provides detailed calculations, interpretations, and conclusions, offering valuable insights into statistical analysis and its application in financial decision-making.
1 out of 7












![[object Object]](/_next/static/media/star-bottom.7253800d.svg)