Statistics for Managerial Decisions Assignment - Semester 1

This document presents solutions to a statistics assignment focused on managerial decisions. It includes an analysis of stock data, comparing the performance and risk of RMD and FPH stocks using stem and leaf diagrams, histograms, and return calculations. The assignment also covers the analysis of weekly rent data, exploring variations across different cities using box whisker plots and descriptive statistics. Furthermore, it delves into probability calculations related to crop yields and rainfall patterns. The document also addresses normality tests, confidence intervals, and their application in distinguishing between patient groups with and without heart disease, using statistical methods to analyze and interpret data for informed decision-making. Detailed calculations, interpretations, and graphical representations are provided throughout the solutions.

STATISTICS FOR MANAGERIAL DECISIONS
STUDENT ID:
[Pick the date]

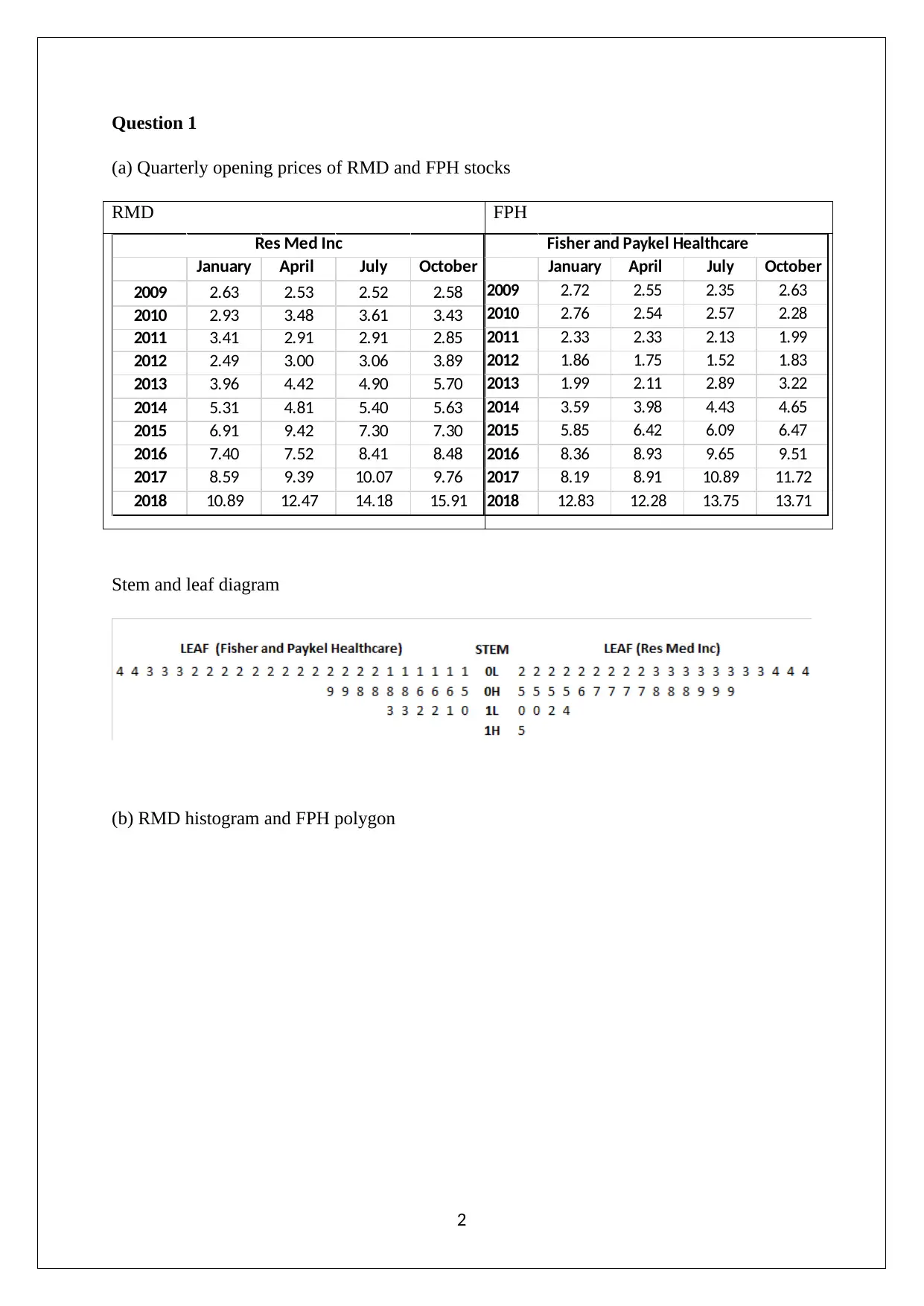
Question 1
(a) Quarterly opening prices of RMD and FPH stocks
RMD FPH
January April July October
2009 2.63 2.53 2.52 2.58
2010 2.93 3.48 3.61 3.43
2011 3.41 2.91 2.91 2.85
2012 2.49 3.00 3.06 3.89
2013 3.96 4.42 4.90 5.70
2014 5.31 4.81 5.40 5.63
2015 6.91 9.42 7.30 7.30
2016 7.40 7.52 8.41 8.48
2017 8.59 9.39 10.07 9.76
2018 10.89 12.47 14.18 15.91
Res Med Inc
January April July October
2009 2.72 2.55 2.35 2.63
2010 2.76 2.54 2.57 2.28
2011 2.33 2.33 2.13 1.99
2012 1.86 1.75 1.52 1.83
2013 1.99 2.11 2.89 3.22
2014 3.59 3.98 4.43 4.65
2015 5.85 6.42 6.09 6.47
2016 8.36 8.93 9.65 9.51
2017 8.19 8.91 10.89 11.72
2018 12.83 12.28 13.75 13.71
Fisher and Paykel Healthcare
Stem and leaf diagram
(b) RMD histogram and FPH polygon
2

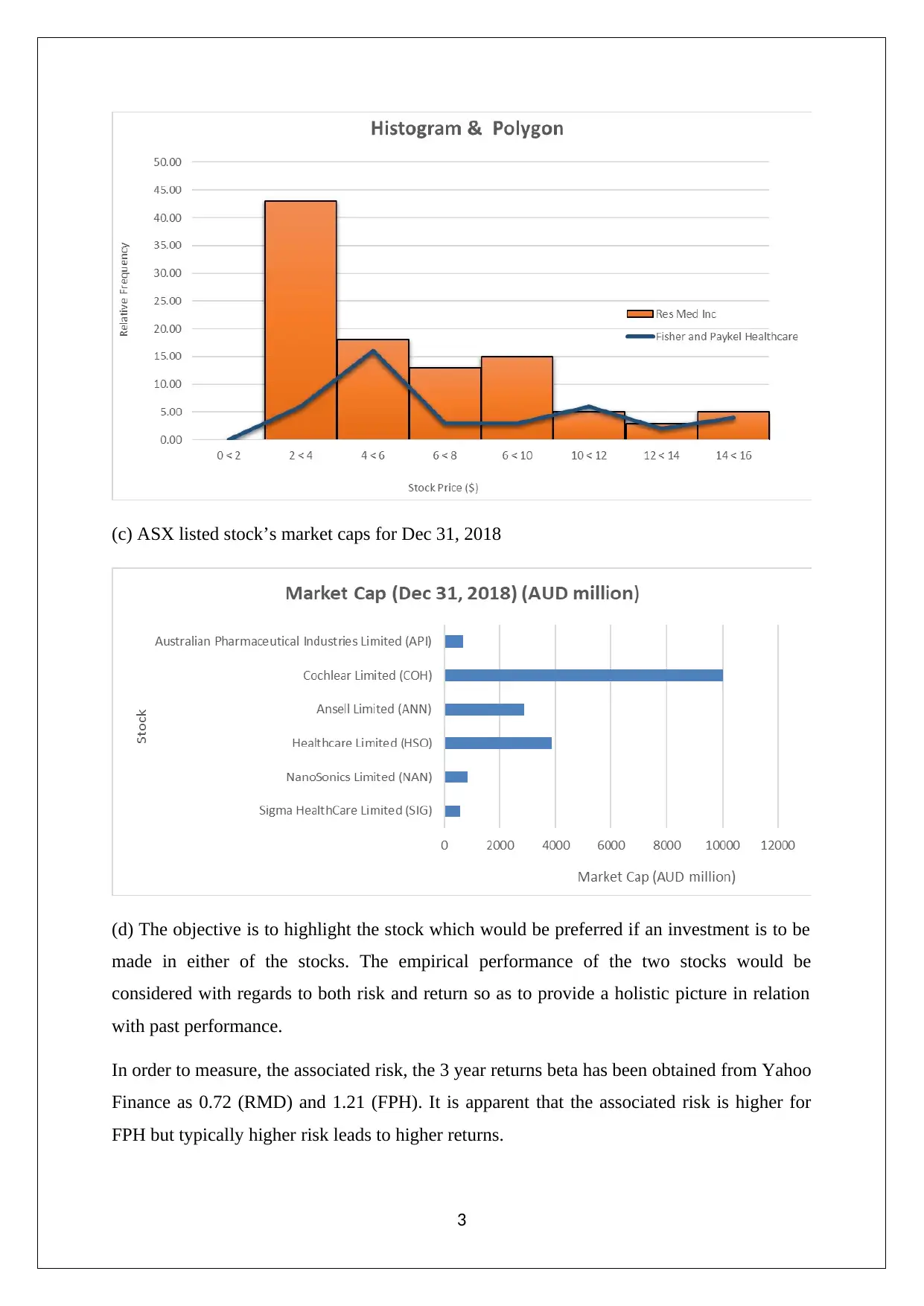
(c) ASX listed stock’s market caps for Dec 31, 2018
(d) The objective is to highlight the stock which would be preferred if an investment is to be
made in either of the stocks. The empirical performance of the two stocks would be
considered with regards to both risk and return so as to provide a holistic picture in relation
with past performance.
In order to measure, the associated risk, the 3 year returns beta has been obtained from Yahoo
Finance as 0.72 (RMD) and 1.21 (FPH). It is apparent that the associated risk is higher for
FPH but typically higher risk leads to higher returns.
3

The returns considering the current price and the price three years ago for the two stocks
under consideration have been computed as illustrated below.
It is evident that RMD stock not only has given superior returns over the period under
consideration but also has lower risk which makes it a preferred bet ahead of FPH.
Question 2
(a) Weekly rent mean, median, first quartile (Q1) and third quartile (Q3)
(b) Weekly rent range, standard deviation and mean absolute deviation
(c) Box whisker plot
4

(d) The corresponding listings from airbnb were checked to ascertain weekly rent for the
given cities. The following observations were made.
 The amount of listings available in the form a apartment with one room varied
significantly across cities with maximum availability in Sydney and Melbourne. This
might be related to the higher rent in these cities.
 The weekly rent for eligible properties for each geography showed immense variation
based on amenities attached and the precise location of the property. Therefore, an
exact comparison of the prices with the sample is not feasible. However, the variation
observed in the weekly rent prices is quite high.
Question 3
(a
)
Prob (Canola field | Australia)
P =2538678/ (4623527+2538678+371339+955321+11720277)=0.1256
(b
)
Prob (Truck of Wheat | New South Wales)
= 9556517/ ((2755310+1201045+403121+483081+9556517)) =0.6637
(c
)
Prob (Crop of barley | South Australia)
Yield of crop = Production of crop / Area of crop
5

(e) The unreliability in the estimates provided by ABS is captured by the relative standard
error. It has been stated that the estimates related to grain sorghum in South Australia are
too unreliable for general use since it has the largest relative standard error which
amounts to higher than 50%.
Question 4
(a) Total rainfall days in the given year = 170
Number of weeks = 52
Mean x = 172 / 52 = 3.3077 rainfall per week
(i) P(0) “Zero rainfall in a week”
(ii) P(X> = 3) “3 or more days of rainfall in week”
6

(b) Average rainfall and standard deviation of rainfall of the given year
(i) P (rainfall between 10 and 50 mm)
(ii) Rainfall amount (X mm)
Z value for 0.12 probability = -1.17499
(-1.17499) = (X- 83.75) / (21.18)
X = required amount for rainfall = 58.86 mmm
Question 5
(a)Test of normality: Normal probability plot
7

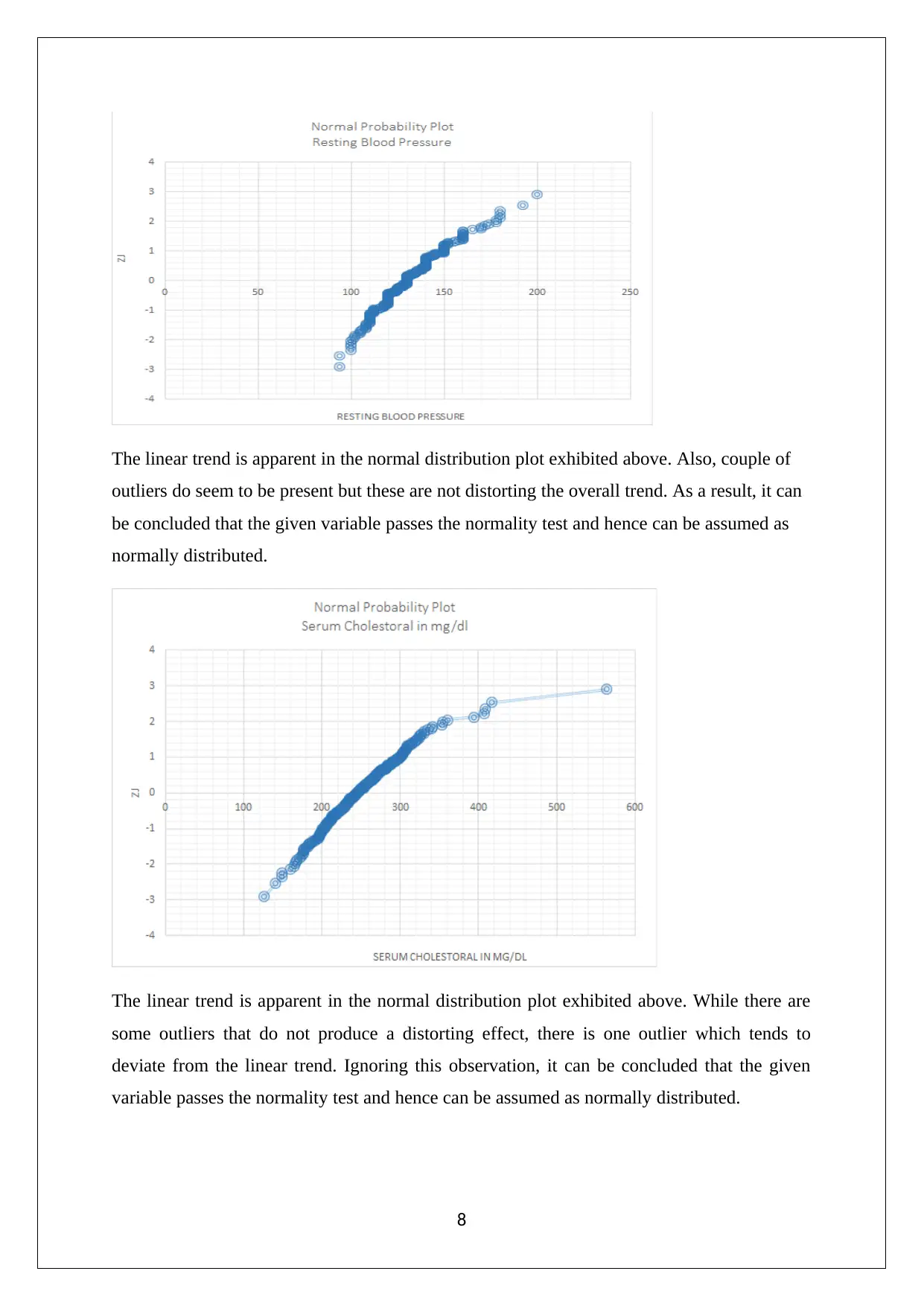
The linear trend is apparent in the normal distribution plot exhibited above. Also, couple of
outliers do seem to be present but these are not distorting the overall trend. As a result, it can
be concluded that the given variable passes the normality test and hence can be assumed as
normally distributed.
The linear trend is apparent in the normal distribution plot exhibited above. While there are
some outliers that do not produce a distorting effect, there is one outlier which tends to
deviate from the linear trend. Ignoring this observation, it can be concluded that the given
variable passes the normality test and hence can be assumed as normally distributed.
8

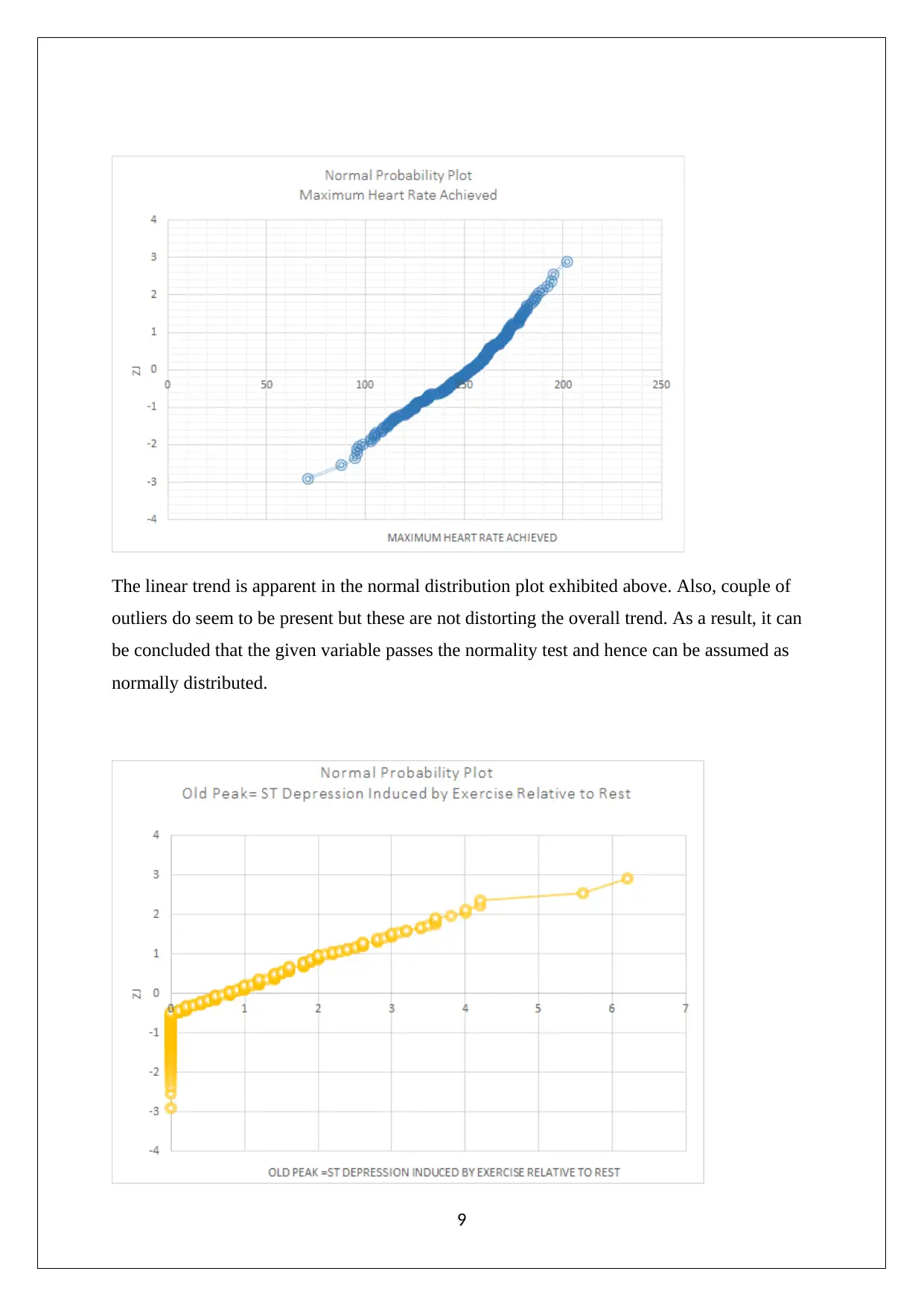
The linear trend is apparent in the normal distribution plot exhibited above. Also, couple of
outliers do seem to be present but these are not distorting the overall trend. As a result, it can
be concluded that the given variable passes the normality test and hence can be assumed as
normally distributed.
9

The linear trend is apparent in the normal distribution plot exhibited above. However, there
are multiple points especially on the lower extreme which distort the overall linear trend.
Clearly these are outliers and ought to be ignored. As a result, it can be concluded that the
given variable passes the normality test and hence can be assumed as normally distributed.
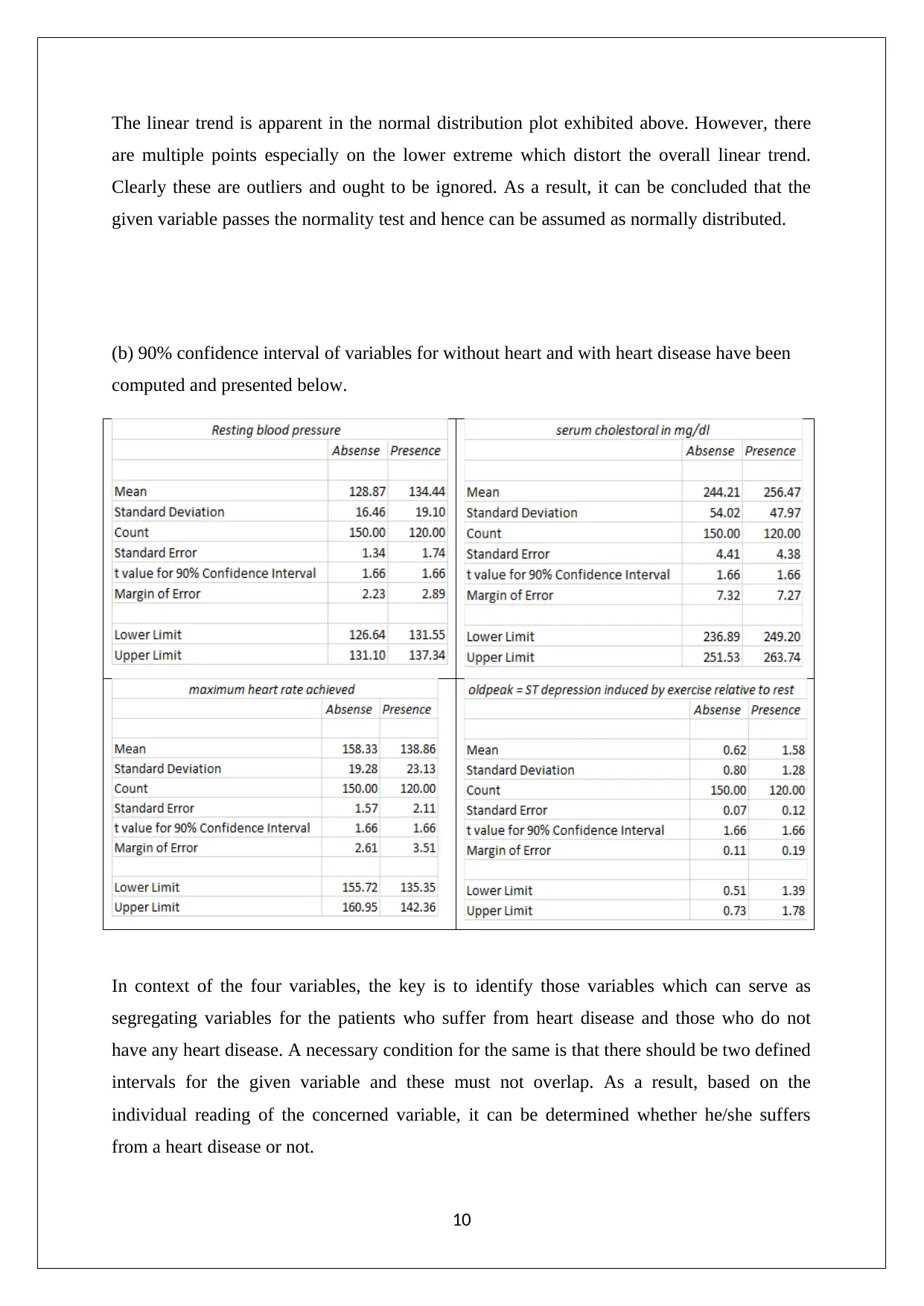
(b) 90% confidence interval of variables for without heart and with heart disease have been
computed and presented below.
In context of the four variables, the key is to identify those variables which can serve as
segregating variables for the patients who suffer from heart disease and those who do not
have any heart disease. A necessary condition for the same is that there should be two defined
intervals for the given variable and these must not overlap. As a result, based on the
individual reading of the concerned variable, it can be determined whether he/she suffers
from a heart disease or not.
10

Taking the above theoretical discussion into consideration, a comparison of confidence
intervals for each of the four variables has been drawn resulting in following conclusion.
1) Resting blood pressure – The intervals for two categories of patient do not overlap
and hence this variable can be used to distinguish.
2) Serum Cholesterol - The intervals for two categories of patient do overlap and hence
this variable cannot be used to distinguish.
3) Maximum heart rate achieved - The intervals for two categories of patient do not
overlap and hence this variable can be used to distinguish.
4) Oldpeak - The intervals for two categories of patient do not overlap and hence this
variable can be used to distinguish.
11