Victoria University STAT 193 Assignment 2: Statistical Analysis [2019]
VerifiedAdded on 2023/01/17
|13
|1843
|22
Homework Assignment
AI Summary
This document provides comprehensive solutions to STAT 193 Assignment 2, a statistics assignment focused on applying statistical concepts to real-world scenarios. The assignment covers a range of topics, including the binomial distribution, normal distribution, hypothesis testing, and confidence intervals. Question 1 explores the classification of random variables, determining whether they fit a binomial distribution. Question 2 delves into binomial probability calculations, including calculating probabilities for specific numbers of successes and failures. Question 3 involves the normal distribution, calculating probabilities and percentiles related to age. Question 4 focuses on standard normal distribution calculations, determining probabilities for various Z-scores. Question 5 addresses hypothesis testing using the sign test and box plots. Question 6 explores confidence intervals and one-sample t-tests to analyze fuel consumption. Finally, Question 7 examines the suitability of paired and one-sample t-tests for different scenarios. The document provides detailed explanations, calculations, and interpretations for each question, making it a valuable resource for students studying statistics.

Statistics in Practice
Assignment 2
STAT 193
[Date]
Assignment 2
STAT 193
[Date]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 1
(a) WOF = 1/6 = 0.1667
This random variable would be categorised as Binomial because each car is independent of
the other cars as there is a specified car only.
(b) The random variable in this case is the length of time that the bulbs work before failing. It
is apparent that there are multiple outputs in this case. The given random variable would
not be considered a binomial distribution since only two outcomes are possible for this
distribution.
(c) The random variable of interest X is the number of rolls unit that he would get a double
six and thus, it can be said that X would take infinite values such as X =2, 3, 4 ,………..
and therefore, it can be concluded that X will not be categorised as binomial.
Question 2
a) The given probability distribution would be binomial. This is because in the given case
there are only two outcomes possible i.e. daily gross amount was more than $ 850 or less
than $850. Further, the performance on each day is independent of the performance
experienced on other days. Also, for each of the days, the probability of registering a
gross amount of over $850 is 0.7.
Here,N (Number of trials) = 20
P (Probability of success) = 0.7
Q (Probability of failure) = 1-0.7 = 0.3
b) Probability of success = 0.70
Number of trials = 20
(i) Probability of exactly 10 business days
P ( X=10 ) =BINOMDIST ( 10 , 20 , 0.70 , FALSE ) =0.031
1
(a) WOF = 1/6 = 0.1667
This random variable would be categorised as Binomial because each car is independent of
the other cars as there is a specified car only.
(b) The random variable in this case is the length of time that the bulbs work before failing. It
is apparent that there are multiple outputs in this case. The given random variable would
not be considered a binomial distribution since only two outcomes are possible for this
distribution.
(c) The random variable of interest X is the number of rolls unit that he would get a double
six and thus, it can be said that X would take infinite values such as X =2, 3, 4 ,………..
and therefore, it can be concluded that X will not be categorised as binomial.
Question 2
a) The given probability distribution would be binomial. This is because in the given case
there are only two outcomes possible i.e. daily gross amount was more than $ 850 or less
than $850. Further, the performance on each day is independent of the performance
experienced on other days. Also, for each of the days, the probability of registering a
gross amount of over $850 is 0.7.
Here,N (Number of trials) = 20
P (Probability of success) = 0.7
Q (Probability of failure) = 1-0.7 = 0.3
b) Probability of success = 0.70
Number of trials = 20
(i) Probability of exactly 10 business days
P ( X=10 ) =BINOMDIST ( 10 , 20 , 0.70 , FALSE ) =0.031
1

(ii) Probability of at least 10 business days
P ( at least 10 ) =1−BINOMDIST ( 9 , 20 , 0.70 ,TRUE )=1−0.017=0.983
(iii) Probability of getting 6 and 16 (inclusive) business days
P ( 6< x <16 )=BINOMDIST ( 16 , 20 ,0.70 , TRUE )−BINOMDIST ( 5 , 20 ,0.70 , TRUE )=0.893−0=0.893
(iv) Probability of fewer 6 business days
P ( X <6 )=BINOMDIST ( 5 , 20 , 0.70 ,TRUE )=0.00004
c) No, based on the given evidence, May should not suspect that the probability of grossing
more than $850 is less than 0.7. This is because the probability of 0.7 is for the population
and hence it would not be necessarily true for each of the samples. However, if the
number of days over which observations are made is increased, then 0.7 probability
would arise.
d) i) Based on the given information, P (X<6) = 0.001612
ii) A value of p where May would not be surprised if the total days grossing more than $ 850
would be less than 6 is 0.4 as P(X<6) in this case would be 0.1256 which implies that the
event is not rate or unexpected.
Question 3
Normal distribution
Mean μ=27.9 year
Standard deviation σ =3.7 years
(a) Proportion of couple with children that have had their first child before the mother is 20
Z value = (20-27.9)/3.7 = -2.14
2
P ( at least 10 ) =1−BINOMDIST ( 9 , 20 , 0.70 ,TRUE )=1−0.017=0.983
(iii) Probability of getting 6 and 16 (inclusive) business days
P ( 6< x <16 )=BINOMDIST ( 16 , 20 ,0.70 , TRUE )−BINOMDIST ( 5 , 20 ,0.70 , TRUE )=0.893−0=0.893
(iv) Probability of fewer 6 business days
P ( X <6 )=BINOMDIST ( 5 , 20 , 0.70 ,TRUE )=0.00004
c) No, based on the given evidence, May should not suspect that the probability of grossing
more than $850 is less than 0.7. This is because the probability of 0.7 is for the population
and hence it would not be necessarily true for each of the samples. However, if the
number of days over which observations are made is increased, then 0.7 probability
would arise.
d) i) Based on the given information, P (X<6) = 0.001612
ii) A value of p where May would not be surprised if the total days grossing more than $ 850
would be less than 6 is 0.4 as P(X<6) in this case would be 0.1256 which implies that the
event is not rate or unexpected.
Question 3
Normal distribution
Mean μ=27.9 year
Standard deviation σ =3.7 years
(a) Proportion of couple with children that have had their first child before the mother is 20
Z value = (20-27.9)/3.7 = -2.14
2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
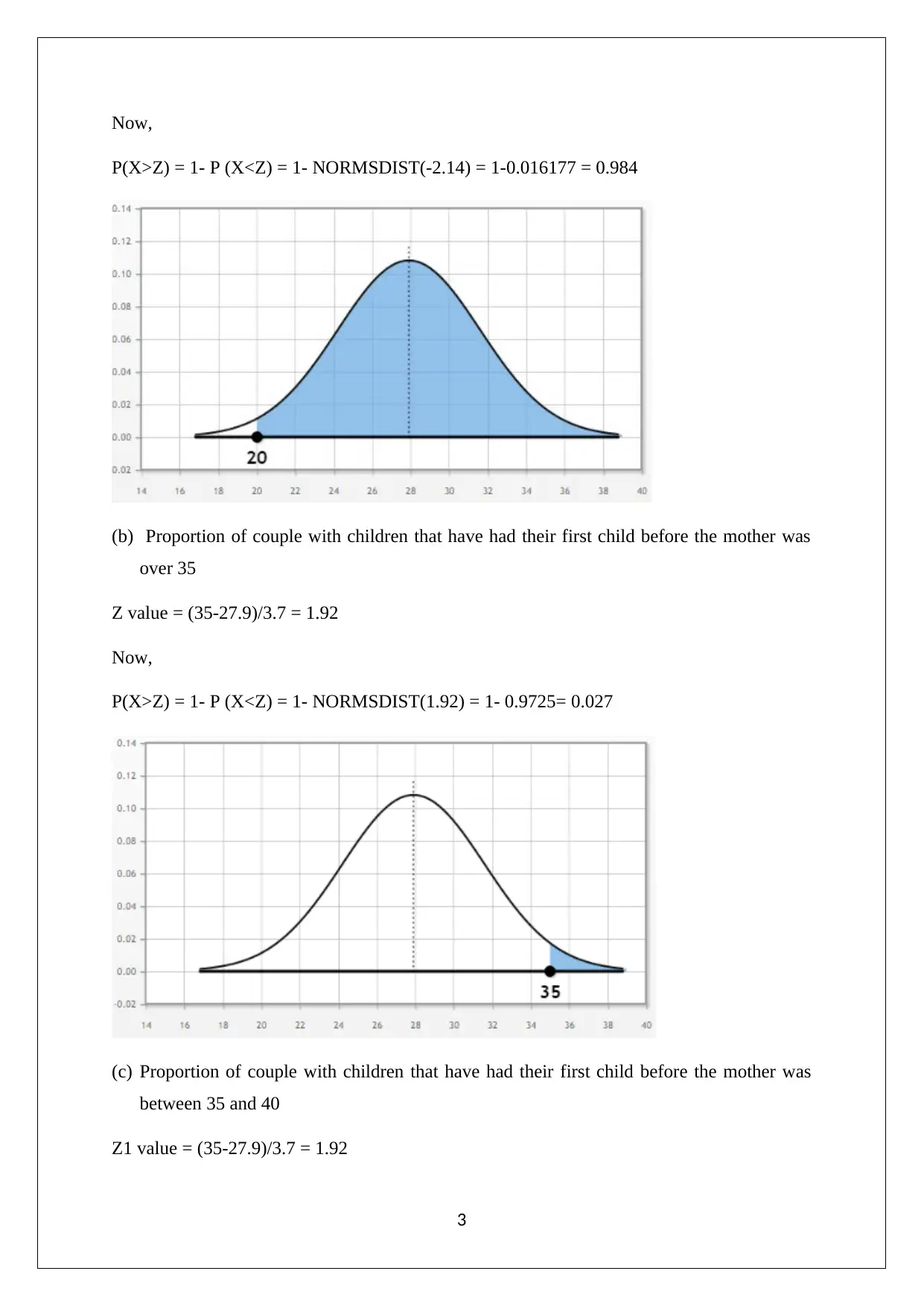
Now,
P(X>Z) = 1- P (X<Z) = 1- NORMSDIST(-2.14) = 1-0.016177 = 0.984
(b) Proportion of couple with children that have had their first child before the mother was
over 35
Z value = (35-27.9)/3.7 = 1.92
Now,
P(X>Z) = 1- P (X<Z) = 1- NORMSDIST(1.92) = 1- 0.9725= 0.027
(c) Proportion of couple with children that have had their first child before the mother was
between 35 and 40
Z1 value = (35-27.9)/3.7 = 1.92
3
P(X>Z) = 1- P (X<Z) = 1- NORMSDIST(-2.14) = 1-0.016177 = 0.984
(b) Proportion of couple with children that have had their first child before the mother was
over 35
Z value = (35-27.9)/3.7 = 1.92
Now,
P(X>Z) = 1- P (X<Z) = 1- NORMSDIST(1.92) = 1- 0.9725= 0.027
(c) Proportion of couple with children that have had their first child before the mother was
between 35 and 40
Z1 value = (35-27.9)/3.7 = 1.92
3
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
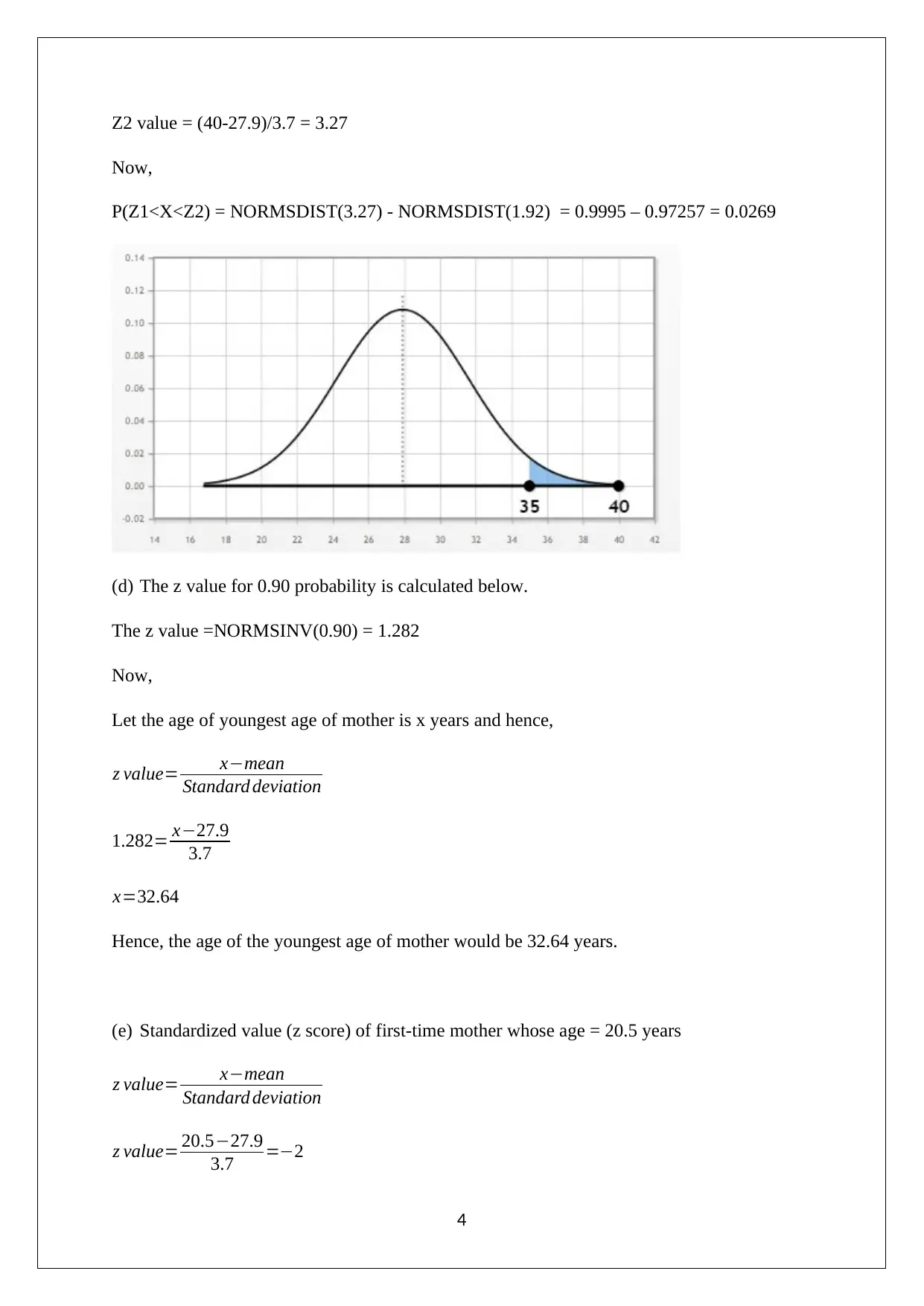
Z2 value = (40-27.9)/3.7 = 3.27
Now,
P(Z1<X<Z2) = NORMSDIST(3.27) - NORMSDIST(1.92) = 0.9995 – 0.97257 = 0.0269
(d) The z value for 0.90 probability is calculated below.
The z value =NORMSINV(0.90) = 1.282
Now,
Let the age of youngest age of mother is x years and hence,
z value= x−mean
Standard deviation
1.282= x−27.9
3.7
x=32.64
Hence, the age of the youngest age of mother would be 32.64 years.
(e) Standardized value (z score) of first-time mother whose age = 20.5 years
z value= x−mean
Standard deviation
z value= 20.5−27.9
3.7 =−2
4
Now,
P(Z1<X<Z2) = NORMSDIST(3.27) - NORMSDIST(1.92) = 0.9995 – 0.97257 = 0.0269
(d) The z value for 0.90 probability is calculated below.
The z value =NORMSINV(0.90) = 1.282
Now,
Let the age of youngest age of mother is x years and hence,
z value= x−mean
Standard deviation
1.282= x−27.9
3.7
x=32.64
Hence, the age of the youngest age of mother would be 32.64 years.
(e) Standardized value (z score) of first-time mother whose age = 20.5 years
z value= x−mean
Standard deviation
z value= 20.5−27.9
3.7 =−2
4
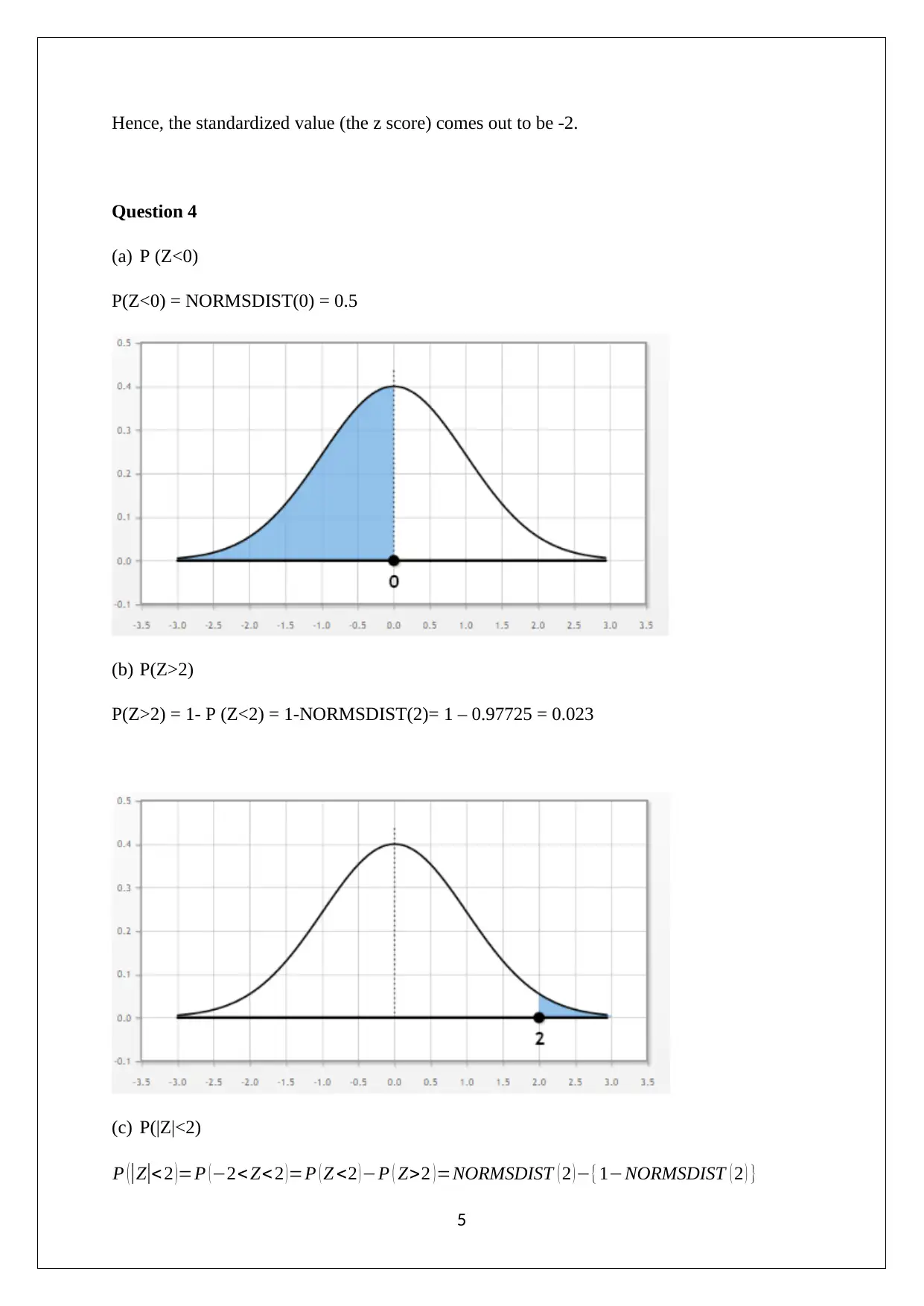
Hence, the standardized value (the z score) comes out to be -2.
Question 4
(a) P (Z<0)
P(Z<0) = NORMSDIST(0) = 0.5
(b) P(Z>2)
P(Z>2) = 1- P (Z<2) = 1-NORMSDIST(2)= 1 – 0.97725 = 0.023
(c) P(|Z|<2)
P (|Z|< 2 )=P ( −2< Z< 2 ) =P ( Z <2 ) −P ( Z>2 ) =NORMSDIST ( 2 ) −{1−NORMSDIST ( 2 ) }
5
Question 4
(a) P (Z<0)
P(Z<0) = NORMSDIST(0) = 0.5
(b) P(Z>2)
P(Z>2) = 1- P (Z<2) = 1-NORMSDIST(2)= 1 – 0.97725 = 0.023
(c) P(|Z|<2)
P (|Z|< 2 )=P ( −2< Z< 2 ) =P ( Z <2 ) −P ( Z>2 ) =NORMSDIST ( 2 ) −{1−NORMSDIST ( 2 ) }
5
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

P (|Z|< 2 )=0.9772−0.02275=0.954
(d) P(|Z|>2)
P (|Z|> 2 )=1−P (|Z |<2 ) =1−0.954=0.046
(e) The probability would be 0.997 when the normal random variable is more than 3 standard
deviation above or below the mean as shown below.
6
(d) P(|Z|>2)
P (|Z|> 2 )=1−P (|Z |<2 ) =1−0.954=0.046
(e) The probability would be 0.997 when the normal random variable is more than 3 standard
deviation above or below the mean as shown below.
6
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Question 5
(a) Hypothesis testing
Step 1: Null and alternative hypothesis
Null hypothesis H0 : Nodifference ∈median of the signed differences
Alternative hypothesis Ha : Median of the signed differences is less than zero .
Step 2: Sign table
Median score on an anger control assessment of group = 42
Step 3: Number of positives and negatives
Number of positive signs = 8
7
(a) Hypothesis testing
Step 1: Null and alternative hypothesis
Null hypothesis H0 : Nodifference ∈median of the signed differences
Alternative hypothesis Ha : Median of the signed differences is less than zero .
Step 2: Sign table
Median score on an anger control assessment of group = 42
Step 3: Number of positives and negatives
Number of positive signs = 8
7

Number of negative signs = 4
Total counts = 8 + 4 = 12
Step 3: Significance level
Given significance level = 0.05
Step 4: The p value
The p value would be computed through Binomial distribution
Number of success = 4
Number of trials = 12
Probability of success = 0.5
The p value =BINOMDIST (4,12,0.5, TRUE) = 0.1938
Step 5: Result
It can be concluded based on the above that the p value is higher than significance level and
thus, insufficient evidence is present to reject the null hypothesis and to accept the alternative
hypothesis. Therefore, it can be said that median of the signed differences is less than zero
Box and whisker plot.
8
Total counts = 8 + 4 = 12
Step 3: Significance level
Given significance level = 0.05
Step 4: The p value
The p value would be computed through Binomial distribution
Number of success = 4
Number of trials = 12
Probability of success = 0.5
The p value =BINOMDIST (4,12,0.5, TRUE) = 0.1938
Step 5: Result
It can be concluded based on the above that the p value is higher than significance level and
thus, insufficient evidence is present to reject the null hypothesis and to accept the alternative
hypothesis. Therefore, it can be said that median of the signed differences is less than zero
Box and whisker plot.
8
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The box plot highlights that the distribution of the underlying variable is skewed which imply
that the distribution is non-normal. Hence, t stat based sign test would be an appropriate
choice. Also, the subjects remain the same.
Question 6
(a) Mean and standard deviation of litres of petrol required
Standard error = Standard deviation / sqrt (sample size) = 0.659/sqrt (30) = 0.1203
(i) 90% confidence interval
The z value for 90% confidence interval =1.64
Margin of error = z value * Standard error = 1.64 * 0.1203 = 0.197
Lower limit = Mean - Margin of error = 9.50 – 0.1974 = 9.30
Upper limit =Mean + Margin of error = 9.50 + 0.1974 = 9.70
9
that the distribution is non-normal. Hence, t stat based sign test would be an appropriate
choice. Also, the subjects remain the same.
Question 6
(a) Mean and standard deviation of litres of petrol required
Standard error = Standard deviation / sqrt (sample size) = 0.659/sqrt (30) = 0.1203
(i) 90% confidence interval
The z value for 90% confidence interval =1.64
Margin of error = z value * Standard error = 1.64 * 0.1203 = 0.197
Lower limit = Mean - Margin of error = 9.50 – 0.1974 = 9.30
Upper limit =Mean + Margin of error = 9.50 + 0.1974 = 9.70
9
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

90% confidence interval = [ 9.30 9.70]
It can be said with 90% confidence that the mean petrol consumption of the car in L/100 km
would fall within the range of 9.30 L/100km and 9.70 L/100km.
(ii) 95% confidence interval
The z value for 95% confidence interval = 1.960
Margin of error = z value * Standard error = 1.96* 0.1203 = 0.236
Lower limit = Mean - Margin of error = 9.50 – 0.1974 = 9.26
Upper limit =Mean + Margin of error = 9.50 + 0.1974 = 9.74
90% confidence interval = [ 9.26 9.74]
It can be said with 99% confidence that the mean petrol consumption of the car in L/100 km
would fall within the range of 9.26 L/100km and 9.74 L/100km.
(b) Significance level = 0.10
Null and alternative hypothesis
Null hypothesis H0 :μ=9.7
Alternative hypothesis Ha : μ ≠ 9.7
The one sample t test through Inzight has been done and the output is shown below.
10
It can be said with 90% confidence that the mean petrol consumption of the car in L/100 km
would fall within the range of 9.30 L/100km and 9.70 L/100km.
(ii) 95% confidence interval
The z value for 95% confidence interval = 1.960
Margin of error = z value * Standard error = 1.96* 0.1203 = 0.236
Lower limit = Mean - Margin of error = 9.50 – 0.1974 = 9.26
Upper limit =Mean + Margin of error = 9.50 + 0.1974 = 9.74
90% confidence interval = [ 9.26 9.74]
It can be said with 99% confidence that the mean petrol consumption of the car in L/100 km
would fall within the range of 9.26 L/100km and 9.74 L/100km.
(b) Significance level = 0.10
Null and alternative hypothesis
Null hypothesis H0 :μ=9.7
Alternative hypothesis Ha : μ ≠ 9.7
The one sample t test through Inzight has been done and the output is shown below.
10

It can be seen from the above that the p value (0.107) is higher than significance level (0.10)
and thus, the null hypothesis would not be rejected and alternative hypothesis would not be
accepted. Hence, it can be said that mean fuel consumption of the car is not 9.7 L/100km.
(c) Claim: Whether the fuel consumption of driver was lower than NZAA figures.i.e.9.7
L/100km.
Null hypothesis H0 :μ ≥ 9.7
Alternative hypothesis Ha : μ<9.7
Hypothesis testing = One tailed test (Left tailed)
The test statistics (from above output) = -1.6619
Degree of freedom = 30-1 = 29
The rights tailed p value = 0.0537
The significance level is given as 0.1 then as per the above understanding it can be seen that p
value is lower than significance level and thus, null hypothesis would be rejected and
alternative hypothesis would be accepted. Therefore, it can be concluded that the fuel
consumption of driver is less than 9.7 L/100 km.
11
and thus, the null hypothesis would not be rejected and alternative hypothesis would not be
accepted. Hence, it can be said that mean fuel consumption of the car is not 9.7 L/100km.
(c) Claim: Whether the fuel consumption of driver was lower than NZAA figures.i.e.9.7
L/100km.
Null hypothesis H0 :μ ≥ 9.7
Alternative hypothesis Ha : μ<9.7
Hypothesis testing = One tailed test (Left tailed)
The test statistics (from above output) = -1.6619
Degree of freedom = 30-1 = 29
The rights tailed p value = 0.0537
The significance level is given as 0.1 then as per the above understanding it can be seen that p
value is lower than significance level and thus, null hypothesis would be rejected and
alternative hypothesis would be accepted. Therefore, it can be concluded that the fuel
consumption of driver is less than 9.7 L/100 km.
11
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 13
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




