Probability and Statistics Assignment - Semester 1, University
VerifiedAdded on 2022/09/09
|12
|290
|19
Homework Assignment
AI Summary
This assignment covers key concepts in probability and statistics. Part 1 focuses on probability, including urn problems, calculating probabilities of different events, and analyzing the number of times an event occurs. Part 2 addresses mathematical statistics, including calculating the mean and variance, exploring probability distributions, and graphing functions. The assignment explores various scenarios, providing detailed solutions and calculations for each problem. The solutions include graphical representations and the application of relevant formulas to arrive at the correct answers. The assignment addresses a range of statistical techniques, including the analysis of probability distributions and the application of statistical methods to solve complex problems. The solutions are presented in a clear and concise manner, making it easy to understand the steps involved in solving each problem.
1 out of 12







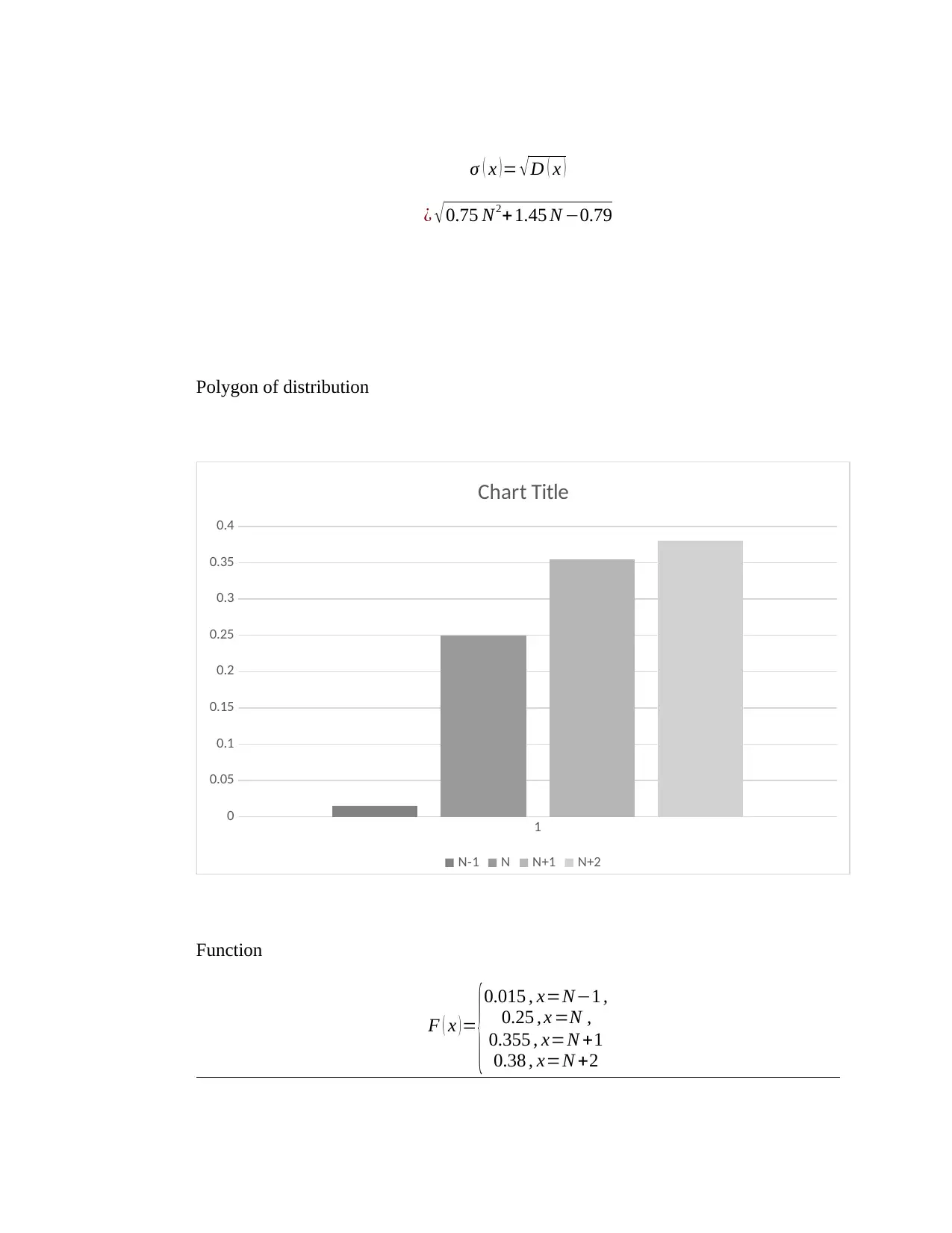
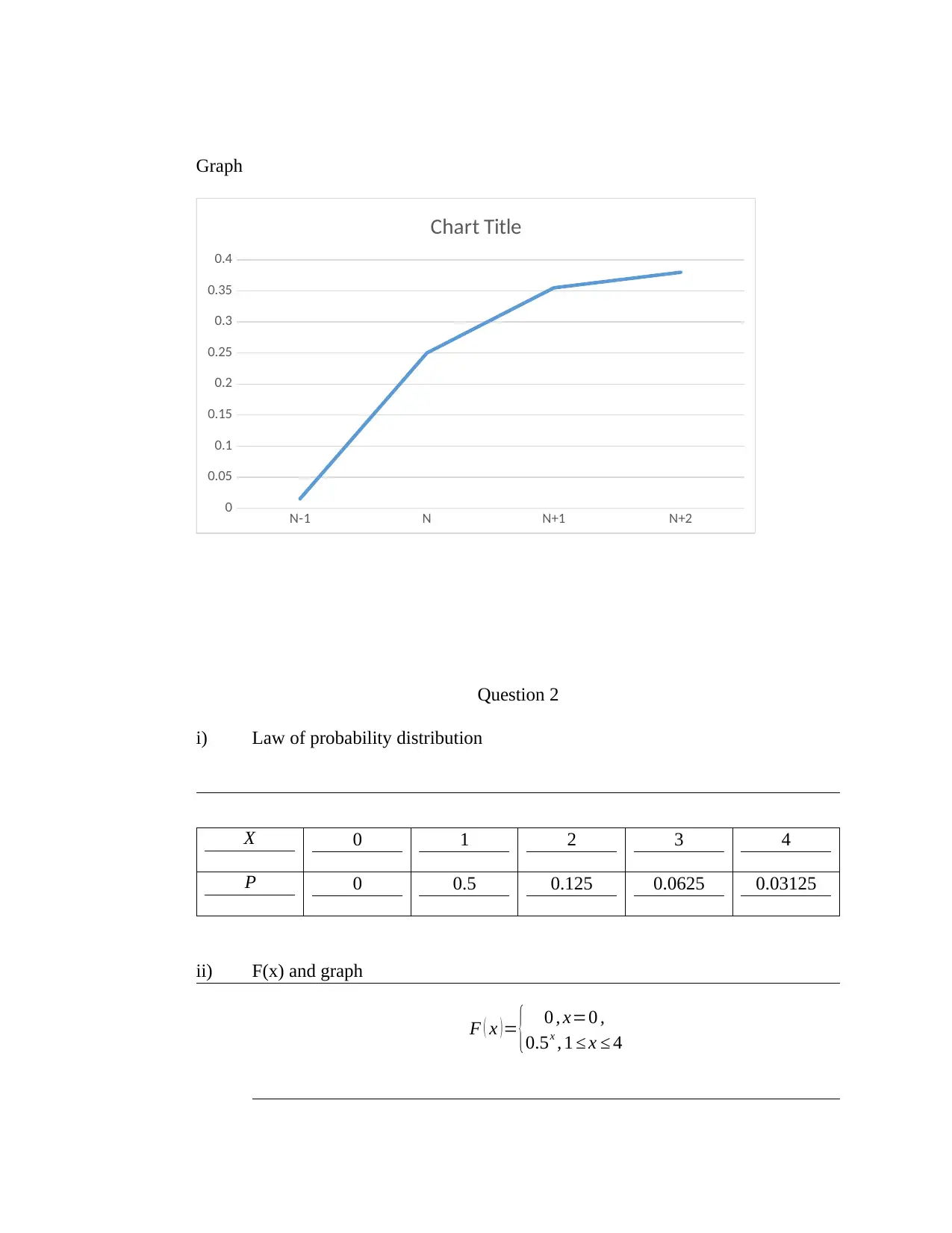
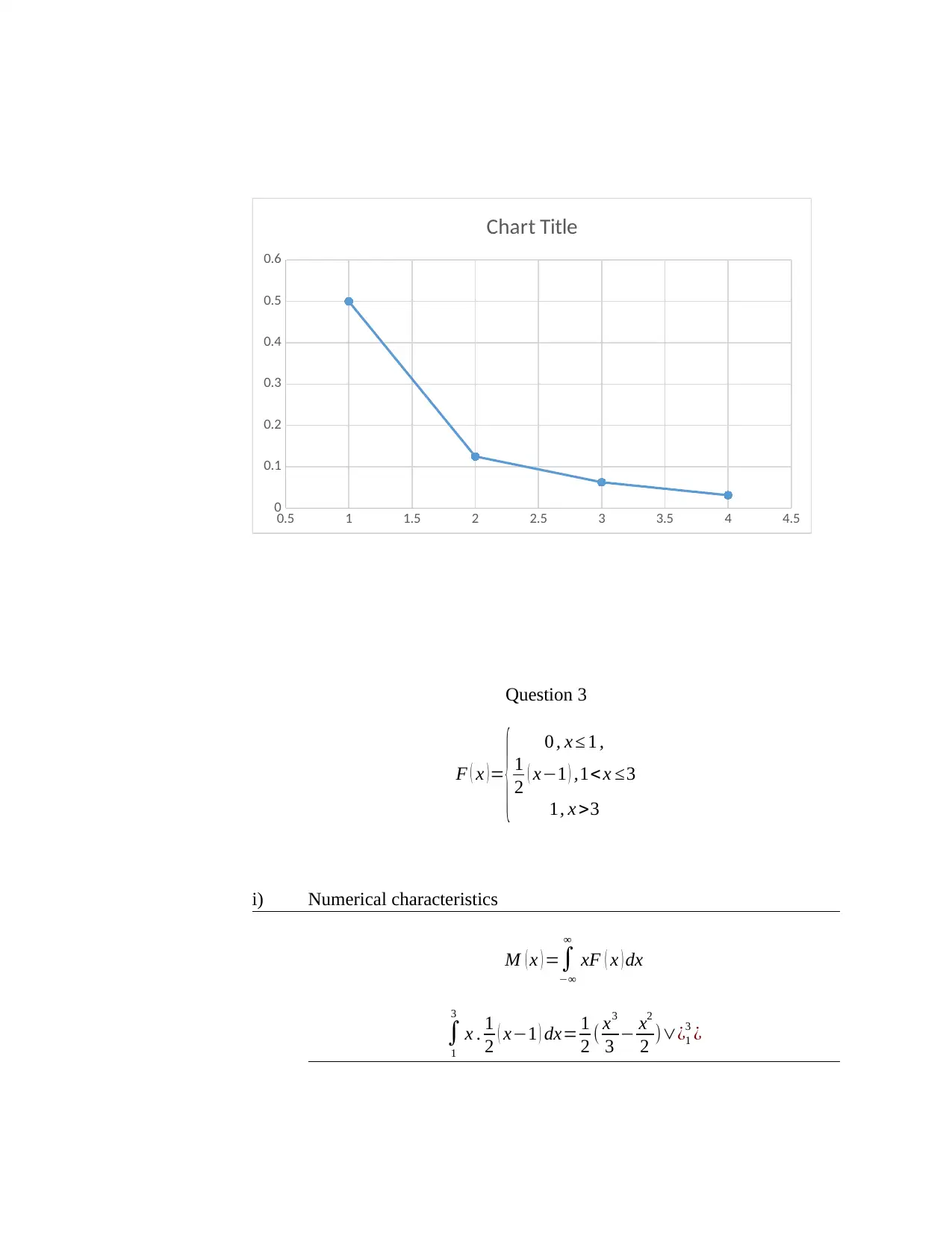

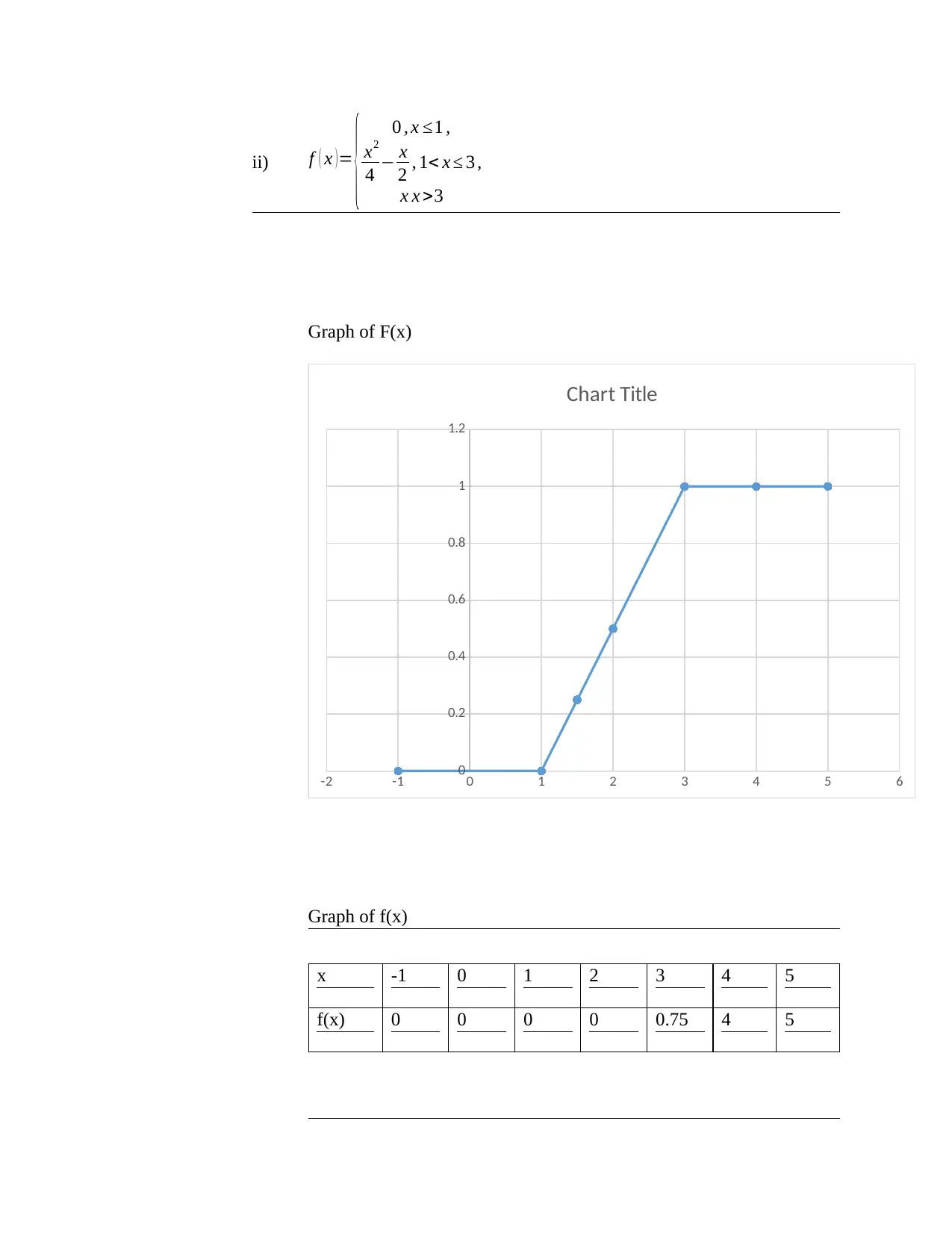



![Victoria University STAT 193 Assignment 2: Statistical Analysis [2019]](/_next/image/?url=https%3A%2F%2Fdesklib.com%2Fmedia%2Fimages%2Fmo%2F8abe3bdd12554d29ac9ec825d7ccd9ee.jpg&w=256&q=75)


![[object Object]](/_next/static/media/star-bottom.7253800d.svg)