Statistics Assignment: Probability, Bayes, and Distributions
VerifiedAdded on 2020/03/23
|9
|1018
|77
Homework Assignment
AI Summary
This statistics assignment addresses several key concepts in probability and statistics. It begins with probability calculations involving damaged fruits from different countries and then explores conditional probability using Bayes' theorem in a scenario involving defective springs from different machines. The assignment covers binomial distributions, calculating probabilities, and expected values. It also delves into geometric distributions, calculating probabilities of success, and the concept of expected value in this context. Further, the assignment explores Poisson distributions and gamma distributions, deriving equations and performing calculations. The assignment concludes with an analysis of normal distributions, including transformations and their impact on the distribution parameters. Throughout the assignment, various formulas and theorems are applied to solve the problems, providing a comprehensive overview of statistical principles.
1 out of 9







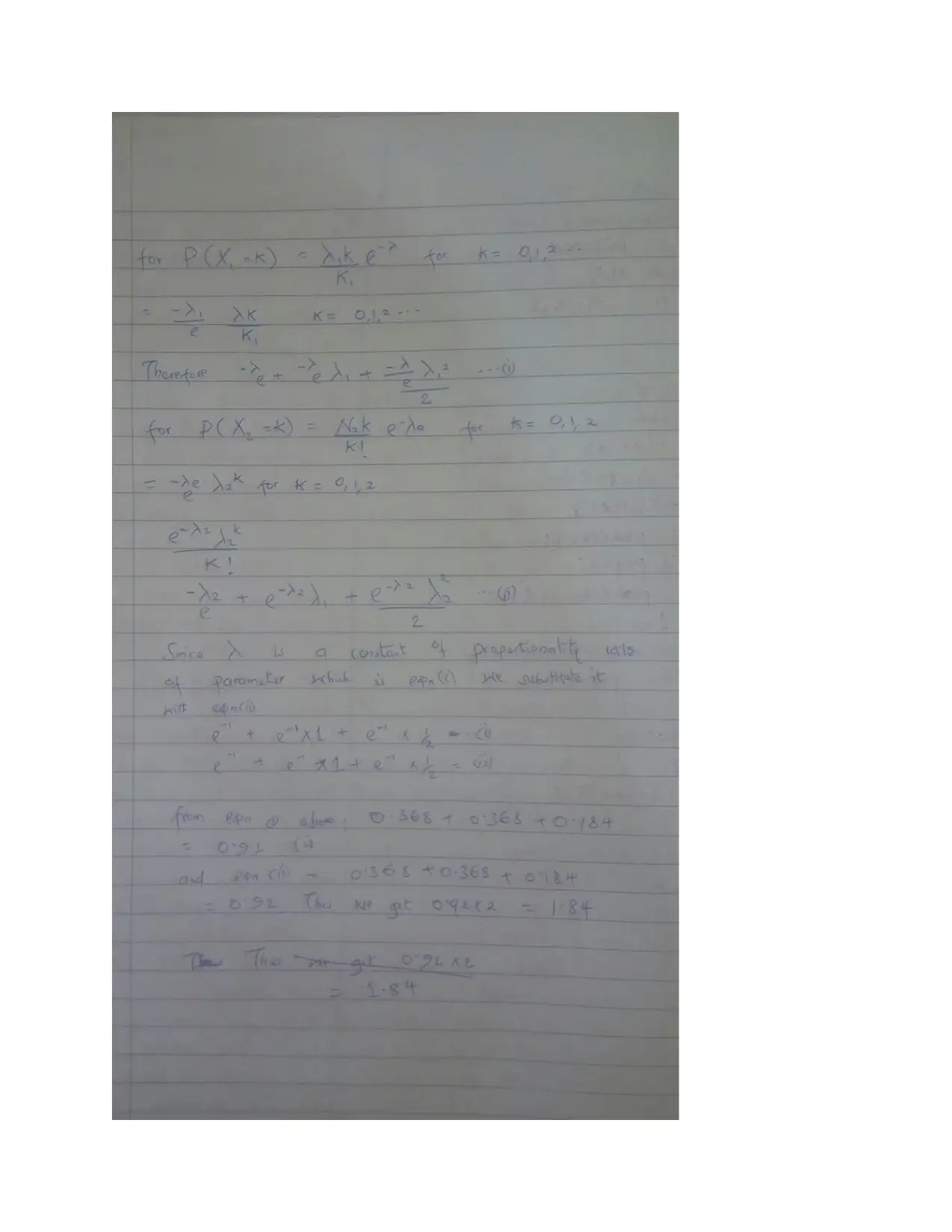





![[object Object]](/_next/static/media/star-bottom.7253800d.svg)