Probability and Statistics Assignment: Solutions and Analysis - 2020

This document presents a comprehensive solution to a Mathematics assignment focusing on probability and statistics. The assignment covers a range of topics, including conditional probability, calculating probabilities in different scenarios (like the gender of children), and understanding cumulative probability distribution functions. It delves into expected values, variance, and moment-generating functions, demonstrating their application in solving statistical problems. Furthermore, the solution explores the diffusion equation, transition density, and long-run probabilities, providing a complete analysis of the concepts. The assignment is a valuable resource for students studying probability and statistics, offering detailed explanations and step-by-step solutions to enhance understanding and problem-solving skills.

Mathematics Assignment:
Student Name:
Instructor Name:
Course Number:
5th January 2020

Q1i)
Let A and B be the events that the other kid is a girl and one of the kids is a girl respectively.
P (A|B) is the probability of A occurring given that B occurred while P (B) is the probability of B.
A ∩ B Is both kids are girls.
P (A|B) = P ( A ∩B)
P( B)
P ( A ∩B ) = 1
2 × 1
2 = 1
4
P (B) = 3
4
P (A|B) = P (A ∩B)
P(B) =
1
4
3
4
= 1
4 × 4
3 =1
3
P (A|B) ¿ 1
3
ii)
Let B and G be the events of being a boy and a girl respectively.
In three births, the possible outcomes are BBB, BBG, BGB, BGG, GBB, GBG, GGB and GGG.
This gives 8 possibilities. Out of the two children already born, one must be a girl. Besides this, the
third child must also be a girl. From the above 8 outcomes, the only outcomes satisfying these two
conditions (Out of the two children already born, one must be a girl and the third child being a girl) are
BGG and GBG. These are 2 outcomes.
P (third being girl given one kid is a girl) = P ( BGG∨GBG )= 2
8 = 1
4
iii)
P(X=xn|x> x1 )=P ( X=x2 ) + P ( X=x3 ) + P ( X =x4 ) +…+ P ( X=xn )

P(X= xn| x> x1 )=∑
n¿2
N
P ( X=xn )=∑
n¿2
N
Pn
iv)
Cumulative probability distribution function f X ( x ) is given by the relation
f X ( x )=P ( X ≤ x )
= f X ( x ) −f X ( x−ε )
= PX ( x ) =P ( x )
For continuous random variable we shall have
FX ( x ) = ∫
x− ε
2
x+ ε
2
f X ( t ) dt
P ( x )=Pr ( X ∈(x− ε
2 , x + ε
2 ))
Pr ( X ∈( x − ε
2 , x + ε
2 ))= ∫
x− ε
2
x+ ε
2
f X ( t ) dt
Let f X ( t ) =t
Pr ( X ∈( x − ε
2 , x + ε
2 ))= ∫
x− ε
2
x+ ε
2
t dt
=Pr ( X ∈( x − ε
2 , x + ε
2 ))=( t2
2 )x− ε
2
x+ ε
2
Pr ( X ∈( x − ε
2 , x + ε
2 ))=1
2 ( (x+ ε
2 )2
−(x− ε
2 )2
)
= 1
2 ( x2+ xε−0.25 ε 2−x2+xε −0.25 ε2 ) =xε
=Pr ( X ∈( x − ε
2 , x + ε
2 ))=P ( x ) =xε
P' ( x )=ε

lim
ε → 0
Pr ( X ∈(x− ε
2 , x+ ε
2 ) )=lim
ε → 0
xε=0
But P' ( x )=ε=0 since ε is a very small value.
lim
ε → 0
Pr (X ∈( x− ε
2 , x+ ε
2 ) )=P' ( x )=0Hence shown.
v)
Taking f X ( x ) as the probability density function we have
P(X=|X> a )=∫
a
∞
f X ( x ) dx
P(X=|X>a )=∫
a
∞
f X ( x ) dx
Q2i)
∫
0
z
1
√2 π e−0.5x2
dx
1
√2 π ∫
0
z
e−0.5 x2
dx
Let u= 1
√2 x
dx= √2 xdu
1
√2 π ∫
0
z
e−0.5 x2
dx
= 1
√2 π [ √π
√2 ∫
0
z
2 e−u2
√π du ]
= 1
√ 2 π × √ π
√ 2 [ ∫
0
z
2 e−u2
√ π du ]

=
√ π
4 π [∫
0
z
2 e−u2
√π du ]
= 1
2 [ erf (u) ]0
z
= 1
2 [ erf ( x
√ 2 ) ]0
z
¿ 1
2 erf ( z
√2 )+C
C is a constant.
ii)
E (Z |Z< 0 ) =μ−σ ∅ (t)
ϑ (t)
Where ϑ ¿) is the cumulative distribution function.
E (Z |Z> 0 )=μ−(μ−σ ∅ (t)
ϑ (t) )=σ ∅ (t )
ϑ (t)
When δ =1
E (Z |Z> 0 )=σ ∅ (t)
ϑ (t) = ∅ (t)
ϑ (t)
E (Z |Z> 0 )=σ ∅ (t)
ϑ (t) = ∅ (t)
ϑ (t)
E (Z |Z> 0 )= ∅ (t )
ϑ (t) =
1
√2 π e−0.5 x2
1
2 erf ( z
√2 )
E (Z |Z> 0 )=
1
√2 π e−0.5 x2
1
2 erf ( x
√2 )
iii)
E (Z |Z< 0 ) =μ−σ ∅ (t)
ϑ (t)

Taking σ =1 andμ=0
E (Z |Z< 0 )=μ−σ ∅ (t)
ϑ (t) =0−σ ∅ ( t)
ϑ (t ) =−∅ (t)
ϑ (t)
E (Z |Z< 0 )=−∅ (t)
ϑ (t) =
− 1
√2 π e−0.5 x2
1
2 erf ( x
√2 )
Q3i)
Suppose t= T −μ
σ and z= X −μ
σ
X=μ+ zσ
E (z ≤ t ¿=E( μ+ zσ )∨z ≤ t ¿
Simplifying the above expression we get
μE ( 1|z ≤ t )+ σ∨E ( z|z ≤ t )
= μ ∫
−∞
t
∅ ( z ) dz+ σ ∫
−∞
t
z ∅ ( z ) dz
= μ ∫
−∞
t
∅ ( z ) dz +σ ∫
−∞
t
z ∅ ( z ) dz
P( z ≤ t)
But ∅ ( z ) dz=ϑ ' ( z ) dz , P ( z ≤ t ) =ϑ (t ) and −z ∅ ( z ) dz=ϑ' ( z ) dz where ϑ is the cumulative distribution
function.
Hence we shall have
μ ∫
−∞
t
∅ ( z ) dz +σ ∫
−∞
t
z ∅ ( z ) dz
P(z ≤ t) =
μ ∫
−∞
t
ϑ ' ( z ) dz−σ ∫
−∞
t
∅ ( z ) dz
ϑ (t)
= μ−σ ∅ (t )
ϑ (t)
Setting σ =1 and μ=0
μ−σ ∅ (t )
ϑ (t) =0−1 ∅ (t)
ϑ (t ) =−∅ (t)
ϑ (t)
However we from calculus that

∫
a
b
F' ( z ) dz=F ( b ) −F (a)
−∅ (t )
ϑ (t) =−∅ ( b )−∅ (a)
ϑ ( b )−ϑ (a)
=− [ ∅ ( b )−∅ (a) ]
ϑ ( b )−ϑ (a)
= ∅ ( a ) −∅ (b)
ϑ ( b ) −ϑ ( a)
ii)
Suppose z= X −μ
σ
When x=0
X= μ+ zσ
E (X¿ X > 0¿=E( μ+Zσ )
¿ E ( μ+ Zσ )=E ( μ¿+ σE(Z ) )
But E ( μ )=μ and also from Z= X−μ
σ When x=0 we get Z=−μ
σ
E ( μ¿+ σE(Z ) )=μ+ σE(Z)
E (X¿ X > 0¿=μ+ σE(Z ∨Z > −μ
σ )
iii)
E( Z )=∅
ϑ Where ϑ is the cumulative distribution function.
E(X) = μ ( 1−2ϑ ( −μ
σ ) +2 σ ∅ ( μ
σ ) )
E(X) = ( μ−2 μϑ ( −μ
σ ) +2 σ ∅ ( μ
σ ) )
Dividing each term of the right hand side by ϑ we obtain
( μ
ϑ − 2 μϑ
ϑ ( −μ
σ ) + 2 ∅
ϑ σ ( μ
σ )
)

μ ( 1
ϑ +2 ( μ
σ ))+¿ 2μE( Z)
But ( 1
ϑ +2 ( μ
σ ) )=1 and 2 μ=σ
μ ( 1
ϑ +2 ( μ
σ ))+¿ 2μE( Z)=μ(1)+¿ σE (Z )
=μ+¿ σE (Z )
E(X) = μ ( 1−2ϑ ( −μ
σ ) +2 σ ∅ ( μ
σ ) )=μ+¿ σE (Z ) hence
E(X) = μ ( 1−2ϑ ( −μ
σ ) +2 σ ∅ ( μ
σ ) )
Var(X) =E ( X2 ¿−¿ ¿
Var(X) =μ2
(1−2ϑ (−μ
σ )2
+2 σ ∅ ( μ
σ )
2
)−
(μ (1−2 ϑ (−μ
σ )+2 σ ∅ ( μ
σ )) )2
Q4i)
Y= ex
Let the median be m.
0.5=∫
0
m
ex dx
0.5=[ ex ]0
m
0.5=em−e0
0.5=em−1
1.5=em
Introducing natural logarithm on both sides
ln 1.5=ln em
0.4055=m
Median ym=0.4055
ii)

y=ex
f X ( x ) =f Y ( y)x=lny ¿ dx
dy ∨¿x=lny ¿
=f Y ( y )=f X ( lny ) . 1
y
= f (lny)
y
The mode of an exponential has mode of 0.
Taking μ as the mode we obtain
f (ln μ)=f (ln 0)=∞
f ' ( lnμ ) = 1
μ = 1
0 =∞
Hence
f ' ( ln μ ) =f (ln μ)
iii)
The factor 1
√2 π in the above expression is makes it possible to have a total area under the curve to be
1.On the other hand, 1
2 in the power will make the distribution to have a variance of 1 and hence a
standard deviation of 1.
Suppose that x is a random variable. Then the expected value of etx is taken as the moment generating
function of y. With normal distribution f, mean μ and deviation σ , the moment generating function M (t)
can be determined as follows.
M(t)=E(e yx ¿=
´
f ( ¿ )=eut e
1
2 σ2
=eμ + 1
2 σ2
Setting t=1
eμ + 1
2 σ (1 )2
=eμ + 1
2
iv)

E(Y) =eμ + 1
2 σ2
Setting σ =1 andμ=0
E(Y) =e0+ 1
2 =e
1
2 =1.649
For a normal distribution the median ym is 0 because it is equal to the mean.
ym=0
The mode μ=0
μ< ym < E (Y )
Q5i)
Let u ( x ,t )=∅ ( x , t )= 1
√2 π e
− x2
2 t
1
2
∂
∂ x ( 1
√2 π e
− x2
2 t
)= 1
2 ( 1
2 erf ( L
√8 t ) )
= 1
4 ( erf ( L
√ 8 t ))
1
4
∂
∂ x (erf ( L
√8 t ) )=
τ [ −2
3 , π x2
( √8 ) ( πt )1.5 ]x
4
3
3 3
√π
+ C
1
2
∂2
∂ y2 u ( x ,t ) =
τ [ −2
3 , π x2
( √ 8 ) ( πt ) 1.5 ] x
4
3
3 3
√ π
+ C
1
2
∂
∂t ( 1
√2 π e
−x2
2 t
)=
τ [ −2
3 , π x2
( √8 ) ( πt )1.5 ]x
4
3
3 3
√ π + C
Therefore ∅ ( x , t ) is a solution to the diffusion equation.
ii)
Since t=0 then ∫
−∞
∞
g ( x ) ∅ ( x , 0 ) dx=0

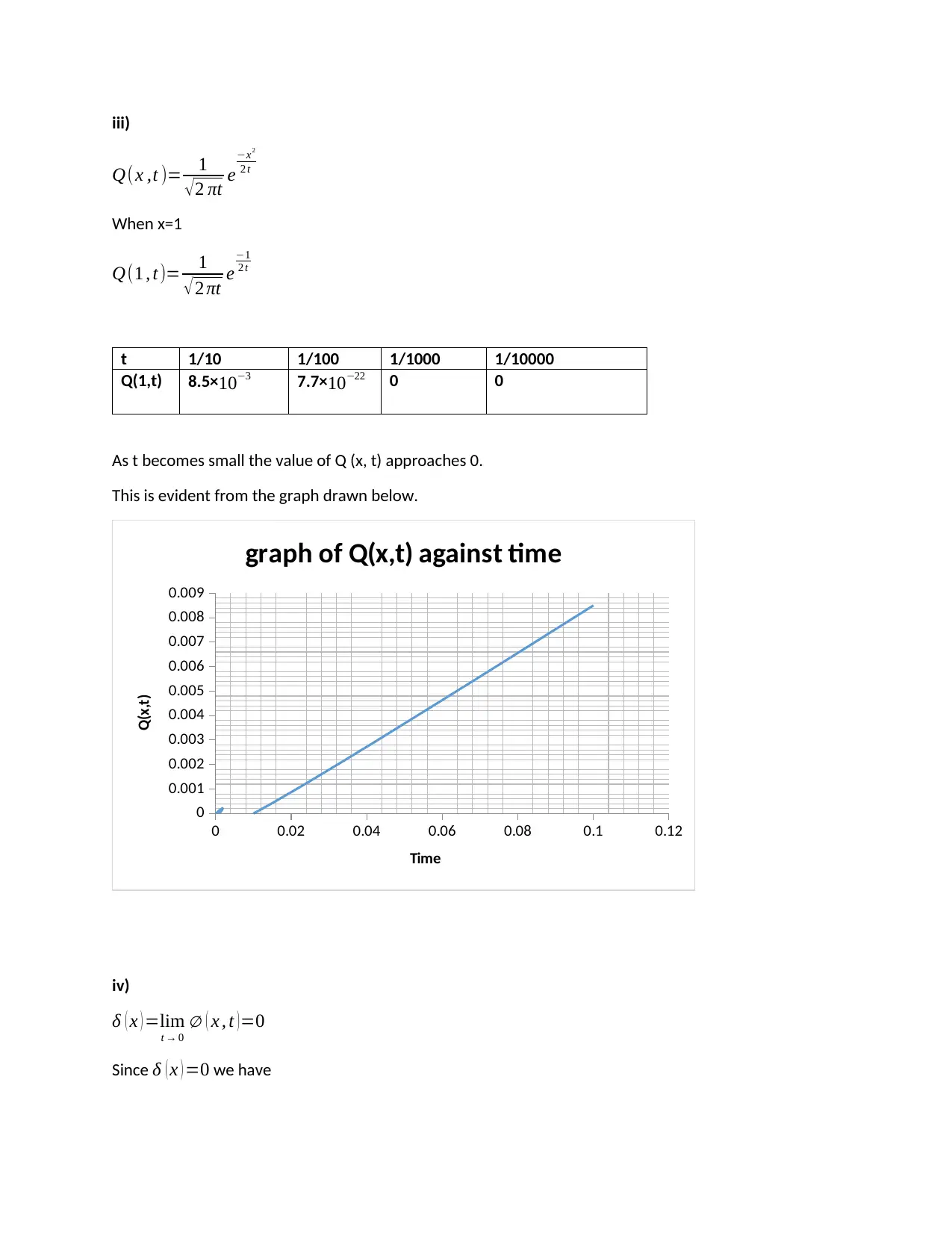
iii)
Q(x ,t )= 1
√2 πt e
−x2
2 t
When x=1
Q(1 , t )= 1
√ 2 πt e
−1
2 t
t 1/10 1/100 1/1000 1/10000
Q(1,t) 8.5×10−3 7.7× 10−22 0 0
As t becomes small the value of Q (x, t) approaches 0.
This is evident from the graph drawn below.
0 0.02 0.04 0.06 0.08 0.1 0.12
0
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
graph of Q(x,t) against time
Time
Q(x,t)
iv)
δ ( x ) =lim
t → 0
∅ ( x , t )=0
Since δ ( x ) =0 we have

∫
−∞
∞
g ( x ) δ ( x ) dx=0
v)
V(x, t) =1+ 2
L ∑
n=1
∞
e
−2 n2 π2
L2
cos √ 4 n2 π2
L2 x
lim
t → ∞
v ( x , t ) =1+ 2
L (0) cos 2nπ
L x=1
Long run transition density is 1.
vi)
Long run probability is given by
∫
0
L
2
1
√ 2 πt e
−x2
2t dx=¿ 1
√ 2 πt
√ t
√ 2 erf ( L
21.5 √ t ) ¿
= 1
√2 πt
√t
√2 erf ( L
√8 t )
= 1
2 erf ( L
√8 t )
vii)
The term with the largest magnitude is t.
Q6i)
d Xt =−μ Xt dt +σd Zt
Let f ( xt , t)=xt eθt
d f (xt , t)=θ xt eθt dt+ eθt d xt
=eθt θμdt +σ eθt d W t
By taking integral from 0 to t we obtain
xt eθt=x0 +∫
0
t
eθs θμds+∫
0
t
1
= x0 e−θt+μ ( 1−e−θt ) +σ

Taking x0=0 and substituting in the above equation we have
xt =¿ (0)e−θt + μ ( 1−e−θt ) + σ
xt =¿ μ ( 1−e−θt ) + σ
ii)
d Xt =b( Xt )dt + σ (X ¿ ¿t )d W t ¿
Let y =p (t , x , y )
By taking the conditional density of Xt given that X 0=x and also that of Xt + s given X s=x.We shall
have
L(θ)=∏
i=1
n
p(ti−t i−1¿ , xi−1 , xi ;θ)¿
iii)
p (x, t)= 1
√2 πv (t) e
−1
2
x2
v (t )
V (t) = σ2
2 μ ( 1−e−2 μt )
At the start t=0 hence
V (0) = σ2
2 μ ( 1−e−2 μt )= σ 2
2 μ ( 1−e−0 ) =0 and also
p (x, t)= 1
√2 πv (0) e
−1
2
x2
v(0) = 1
√2 π ( 0) e−∞=0
1
2 σ2 ∂
∂ x2
2
p ( x , t )+ μ ∂
∂ x ( xp(x , t) )= 1
2 σ 2 ∂
∂ x2
2
( 0 )+ μ ∂
∂ x ( x (0) )
=0+0=0
∂
∂ t ( p (x , t) ) = ∂
∂ t ( 0¿ )=0
1
2 σ2 ∂
∂ x2
2
p ( x , t )+ μ ∂
∂ x ( xp(x , t) )= ∂
∂ t ( p (x , t) ) =0
Therefore p ( x , t ) satisfies the above equation.
iv)

lim
t →0
p (x , t)=lim
t → 0
1
√ 2 πv (t) e
−1
2
x2
v (t )
¿ lim
t →0
1
√2 πv (0) e
−1
2
x2
v (0 )=lim
t →0
1
√ 2 π (0) e
−1
2
x2
(0)=0
lim
t → ∞
p (x , t )=lim
t → ∞
1
√2 πv (∞ ) e
−1
2
x2
v(∞)
But V ( ∞) = σ2
2 μ ( 1−e−2 μ ∞ )= σ 2
2 μ ( 1−e− ∞ )
¿ σ2
2 μ ( 1−e−∞ ) = σ2
2 μ ( 1−0 ) = σ2
2 μ
lim
t → ∞
p (x , t)= 1
√ 2 π ( σ2
2 μ )
e
−1
2
x2
( σ2
2 μ )
= 1
√ π ( σ 2
μ )
e
−x2
( σ 2
μ )
Suppose σ2
μ =k then we shall have
1
√ π k e
−x2
( k )
lim
t → ∞
p (x , t )= 1
√ π k e
− x2
( k )
In the long run the process drifts towards the mean.