Analyzing Stock Returns with Hypothesis Testing - Statistics

This assignment solution focuses on the statistical analysis of stock returns using hypothesis testing. It begins by testing the normality of returns for BA and GD stocks using the Jarque-Bera test, concluding that neither follows a normal distribution. Subsequently, a t-test is applied to assess if the mean returns of GD stock differ from a claimed value. An F-test is then used to determine if there's a significant difference in the risk (variance) between the two stocks. Confidence intervals are constructed to compare the population returns of the stocks. Furthermore, the assignment employs the CAPM model to analyze the relationship between excess returns on the GD stock and the S&P 500 index, including regression analysis, calculation of the coefficient of determination, and hypothesis testing for the beta coefficient. Finally, it tests the normality of residuals from the CAPM model. Desklib offers a wide array of similar solved assignments and study resources for students.

STATISTICS
STUDENT NAME/ID
[Pick the date]

PART A: CALCULATIONS
TASK B
(1) The returns on BA and GD stock along with the index have been computed in line with the
formula provided using the provided data.
1

The objective is to test if the returns of the two stocks are normally distributed or not which
would require Jarque Bera test. The requisite definition of the hypothesis is carried out below.
H0: The distribution of the returns of the given stock does not deviate significantly from
normality.
H1: The distribution of the returns of the given stock does deviate significantly from normality.
For the given test, the significance level has been assumed as 5%.
The relevant test statistics is JB statistic which can be computed on the basis of the formula
highlighted as follows.
By deploying the formula above and the returns of the two stocks, the computation of JB statistic
is shown as follows.
For each of the two stocks, the corresponding JB statistic seems to have exceeded the relevant
critical value of JB parameter at the given significance level. This would imply that the rejection
of H0 is confirmed. This would instead lead to acceptance of H1. The conclusion derived would
be that the distribution of returns for neither of the stocks can be considered as normal.
(2) The hypothesis test above provided evidence of the non-normality of the stock returns.
Owing to this, the GD stock returns distribution would be taken as student t in this case. The
relevant hypotheses to aid this test are indicated as follows.
2

For the given test, the significance level has been assumed as 5%.
Relevant test statistic = T (not Z)
Explanation: The population returns for GD stocks have not been provided and thereby sample
variance is being used.
The Excel based output for hypothesis testing is exhibited as follows.
The p value based approach has been deployed to test the above hypothesis.
The P value (0.0353) does not exceed the significance level for the test which has been taken as
5%. Thus, it is appropriate for the rejection of H0 leading to the acceptance by H1. The logical
conclusion thereby can be drawn that the mean returns on GD stock population would differ
from the claimed valued of 2.8%.
(3) Based on the sample variances, the hypothesis test has been performed to test whether for the
population of returns, there is a significant different in the risk or not.
For the given test, the significance level has been assumed as 5%.
Based on Excel, the appropriate hypothesis test i.e. F test for variance has been performed with
the resultant output pasted below.
3

From the excel output, the relevant p value = 2*One tail p value = 2 *0.016 = 0.032
The P value (0.032) does not exceed the significance level for the test which has been taken as
5%. Thus, it is appropriate for the rejection of H0 leading to the acceptance by H1. The logical
conclusion thereby can be drawn that the variances associated with the population of returns for
the two stocks are different.
(4) The sample returns on the two stocks has been provided but the objective is to draw a
comparison between the population returns of the stocks under consideration.
For the given test, the confidence level has been assumed as 95%.
The requisite approach has to be based on confidence interval. As a result, 95% confidence
interval for both the stock returns has been computed using Excel as the medium. The resultant
output is pasted as shown below.
4

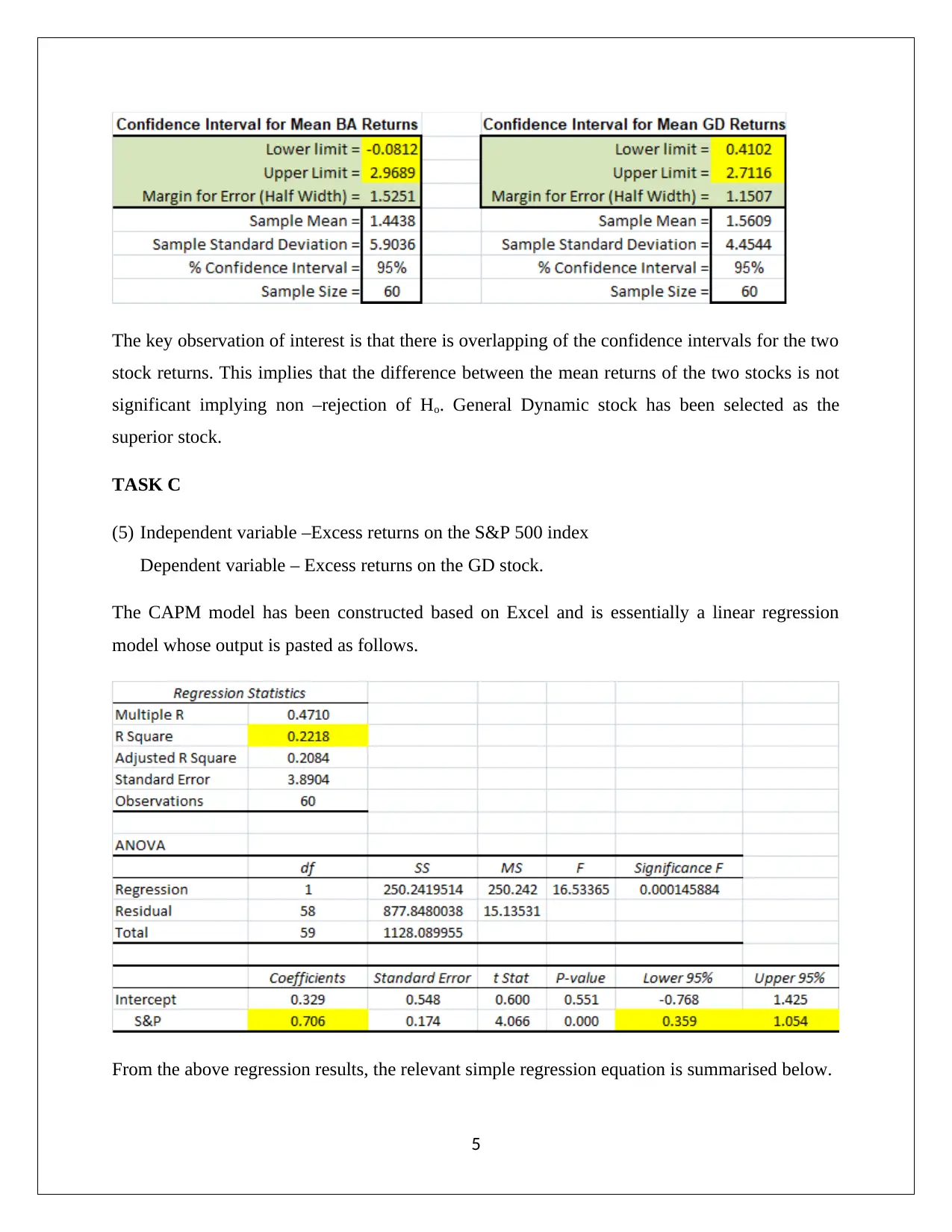
The key observation of interest is that there is overlapping of the confidence intervals for the two
stock returns. This implies that the difference between the mean returns of the two stocks is not
significant implying non –rejection of Ho. General Dynamic stock has been selected as the
superior stock.
TASK C
(5) Independent variable –Excess returns on the S&P 500 index
Dependent variable – Excess returns on the GD stock.
The CAPM model has been constructed based on Excel and is essentially a linear regression
model whose output is pasted as follows.
From the above regression results, the relevant simple regression equation is summarised below.
5

(c) Coefficient of Determination=0.2218
(d) The lower limit of the 95% confidence interval of beta or slope coefficient is 0.36. The upper
limit of the 95% confidence interval of beta or slope coefficient is 1.05.
(6) The testing of significance of beta can be aided based on the following hypothesis.
The hypothesis testing in this case needs to be carried out based on confidence interval. The
decision rule is that H0 is rejected only if the underlying hypothesised value does not lie in the
confidence interval computed for the underlying variable.
Beta 95% confidence interval is denoted by the boundaries (0.36,1.05). The hypothesised value 1
is present in the interval, thereby resulting in non-rejection of H0.
(7) The objective is to test if the residuals obtained in the CAPM model are normally distributed
or not which would require Jarque Bera test. The requisite definition of the hypothesis is carried
out below.
H0: The distribution of the residuals does not deviate significantly from normality.
H1: The distribution of the residuals does deviate significantly from normality.
For the given test, the significance level has been assumed as 5%.
The relevant test statistics is JB statistic which can be computed on the basis of the formula
highlighted as follows.
By deploying the formula above and the sample residuals , the computation of JB statistic is
shown as follows.
6

The corresponding JB statistic seems to have not exceeded the relevant critical value of JB
parameter at the given significance level. This would imply that non-rejection of H0 is confirmed.
The conclusion derived would be that the distribution of residuals can be considered as normal.
As a result, the assumption of linear regression model is fulfilled.
. .
7

PART B: Interpretation
(1) The relevant hypothesis testing has been conducted for testing the distribution of returns for
the two stocks and it can be concluded that neither of these has been found to exhibit normal
distribution.
(2) The hypothesis test based on t test highlights that the average stock returns related to GD
tend to vary in a significant manner from 2.8% and proves that the claim is false.
(3) The relevant hypothesis test for the variances of the given two stocks clearly highlights that
there is difference in the risk associated with each of the two stocks. The stock with the lower
risk can be identified based on the sample variance which is lower the sample returns on the
GD stock. Thereby, GD stock has a lower risk in comparison to BA stock.
(4) Unlike risk, average returns for the two stocks do not seem to indicate any sizable difference.
Typically the preferred stock is one which tends to give superior returns for the similar risk
assumed or when similar returns are offered but for lower risk. Here, GD stock is superior as the
average returns on this stock does not differ from BA but risk is significantly lower, thereby
implying lower risk associated with GD stock.
(5) (b) Based on the CAPM model, the GD stock beta is the slope coefficient which is 0.71. The
interpretation of this coefficient is that a unit change in the market related excess returns would
bring about 0.71% change in the GD excess returns on an average. As the slope coefficient is
positive, hence the direction of change for each of the two stocks remains the same.
(c) The coefficient of determination (0.2218) would mean that variation in GD stock excess
returns to the tune of 22.18% can be accounted for by the corresponding variation in excess
returns on the GD stock. Considering the low predictive ability of the CAPM model there needs
to be other parameters of rsik inserted into the model leading to a multi-factor model.
(d) With a confidence level of 95%, it may be estimated that GD beta would on the higher end
not cross 1.05 while on the lower end it will not cross 0.36.
8

(6) The confidence interval based hypothesis test leas to the conclusion that GD stock is neutral
i.e. beta can be assumed to be 1.
(7) The conclusion derived from hypothesis testing is that the distribution of residuals can be
considered as normal. As a result, the assumption of linear regression model is fulfilled.
9