Introduction to Statistics (STATS 101) Hypothesis Testing Assignment

This document presents a comprehensive solution to a statistics assignment focused on hypothesis testing. The assignment explores various scenarios, including comparing battery life using independent t-tests, analyzing proportions related to cannabis legalization using a t-test for the difference between two proportions, and evaluating productivity scores across different cases. It also examines the impact of spoiler paragraphs on enjoyment ratings using a dependent t-test and investigates the relationship between cyclist age and completion time in a cycling event. The solution provides detailed statistical analyses, including the calculation and interpretation of p-values, confidence intervals, and test statistics, along with discussions on statistical and practical significance. It also includes graphical representations and interpretations to support the findings.

23
Hypothesis Testing
STATS 101/101G/108 Introduction to Statistics
Assignment 3, Second Semester 2018

23
Answer 1:
a) Units: 18
Treatment Variable: Choice of batteries – Energizer and Ultra-cell
Response Variable: Playing time in hours
Two independent groups have to be tested by independent t-test. Let μe and μu be the
average battery life of Energizer and Ultra-cell batteries.
Summary statistics table is as follows,
Table 1: Descriptive Values for Both Batteries
Batteries Mean Std. deviation n
Energizer 8.2789 0.2174 9
Ultra-cell 8.2433 0.1628 9

23
Independent t-test
1. μe - μu = the difference between average playing life time in hours of Energizer and
Ultra-cell batteries.
2. Null Hypothesis: H0: μe - μu =0
3. Alternate Hypothesis: H1: μe - μu ¿ 0 (two-tailed)
4. From summary statistics of the sample survey, xe
−
−xu
−
= 8.2789 - 8.2433 = 0.0356
5. S.E ( xe
−
−xu
−
) = 0.0905 (from t‐procedures tool on Canvas) and the test statistic was
calculated using the formula
t = estimate−hypothesised value
s tan dard error =0 . 3933 as
t= 0. 0356−0
0. 0905 =0 . 3933 with 9 degrees of freedom.
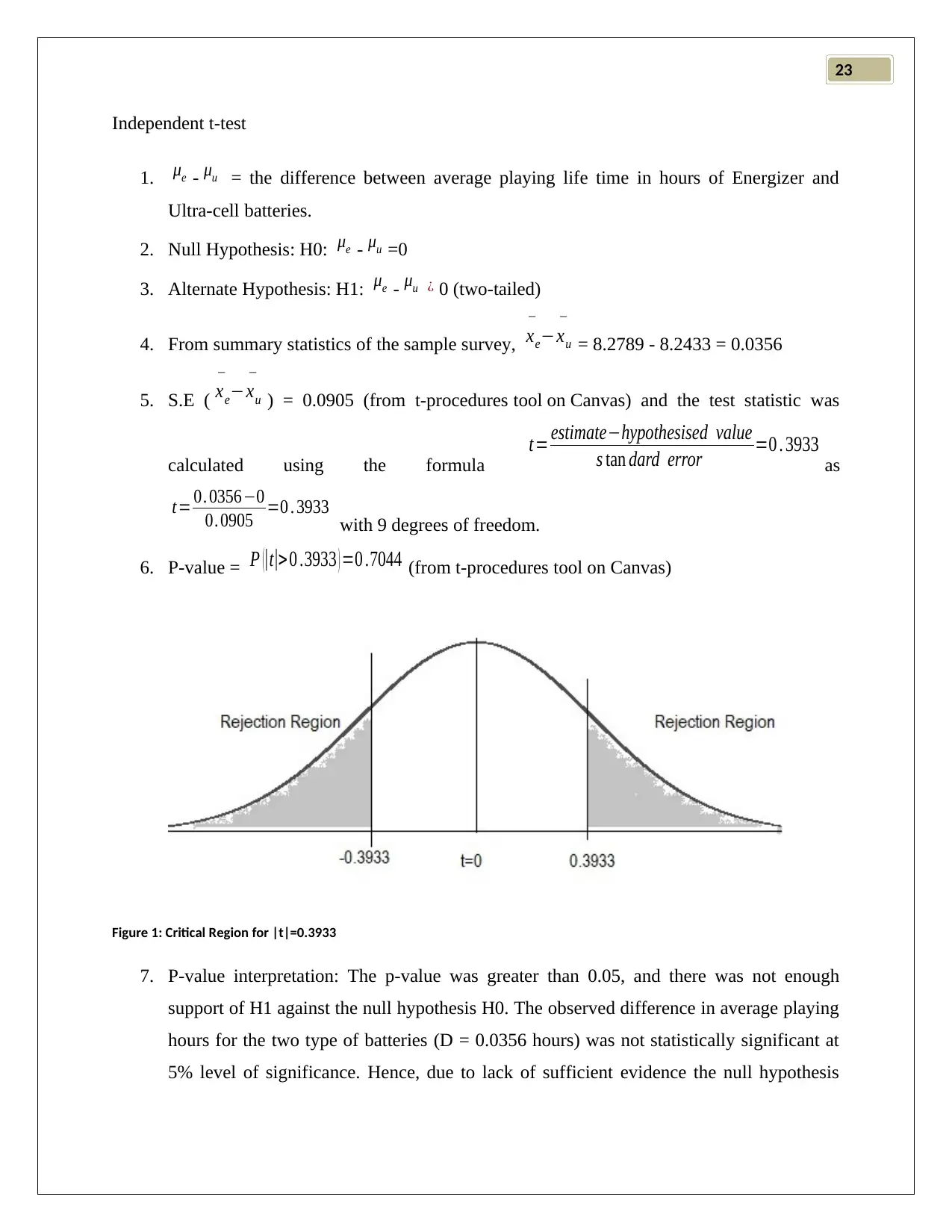
6. P-value = P (|t|> 0 .3933 ) =0 .7044 (from t‐procedures tool on Canvas)
Figure 1: Critical Region for |t|=0.3933
7. P-value interpretation: The p-value was greater than 0.05, and there was not enough
support of H1 against the null hypothesis H0. The observed difference in average playing
hours for the two type of batteries (D = 0.0356 hours) was not statistically significant at
5% level of significance. Hence, due to lack of sufficient evidence the null hypothesis

23
could not be rejected. Therefore, there was no statistically significant difference between
averages of playing time due to both the batteries (Hinton, 2014).
8. Approximate confidence interval at 5% level of significance for μe - μu was calculated
as, CI = ( μe −μu ) ±t multiplier∗SE=0 .0356±2 .306∗0 . 0905= [−0. 1731 , 0. 2443 ] where t-
multiplier was obtained from t‐procedures tool on Canvas.
9. Confidence Interval elucidation: With 95% probability or confidence it can be stated that
the average battery hours of Energizer batteries would be approximately anywhere
between 0.17 hours less than and 0.24 hours more than average battery hours of Ultra-cell
batteries. The right hand limit of the confidence interval of 0.24 hours or approximately
15 minutes would be practically significant result.
10. Conclusion: From the sample data of 9 batteries of both the brands, not enough evidence
was found to establish any significant difference in battery life for playing electronic
game. Though, average battery life of Energizer batteries was greater than that of ultra-
cell batteries, the difference was not statistically significant to opt for any particular
brand.
b) The true value of the parameter was the hypothesized difference in average battery life of
Energizer and Ultra-cell batteries (which was zero). The value of the parameter was well
within the confidence interval (at 5% level of significance), indicating that the conclusion
from p-value was true. The null hypothesis could not be rejected.

23
Answer 2
a) The sampling situation for the particular scenario was: One sample with multiple
inclusive response categories.
b) The sampling for scrutinizing the difference between the estimated proportions of
responses supporting legalizing cannabis- based products and feeling that the law should
stay unchanged was tested by t-test for difference between two proportions.
1. Let py and pn denote the proportions of responses supporting and refuting the legislation.
Hence, py - pn denotes the difference of the two above mentioned proportions.
2. Null hypothesis: H0: py - pn = 0

23
3. Alternate hypothesis: H1: py - pn ¿ 0 (two tailed)
4. Estimated difference: py
^¿
¿ - pn
^¿
¿ =
384
500 −79
500 =0 .61
5. The test statistic formula used
t = estimated difference−hypothesized difference
s tan dard error
For estimated difference = 0.61 and hypothesized difference = 0, the value of the standard
error was calculated using t‐procedures tool on Canvas as S.E ( py
^¿
¿ - pn
^¿
¿ ) = 0.0333 at 5%
level of significance. So the test statistic was calculated as
t = 0. 61−0
0 . 0333 =18 .3183 with
degrees of freedom = ∞
6. P-value = P (|t|> 18. 3183 ) =0. 0000 (from t‐procedures tool on Canvas)
Figure 2: Rejection Region for |t|=18.3183
7. Interpretation of p-value:
The p-value was greater than 0.05 at 5% level of significance and there was enough
evidence in favor of the alternate hypothesis against the null hypothesis. Hence, at 5%
level of significance, evidences from the difference in proportions of
adult New Zealanders in support and against the legislation of cannabis‐based products
usage for medicinal purposes were sufficient to reject the null hypothesis.

23
8. The confidence interval was calculated as
CI =¿ ¿
where t-estimate = 1.96 was obtained from t‐procedures tool on Canvas.
9. Interpretation of Confidence Interval:
The estimated value of difference between the proportions of views in support and in
against of adult New Zealanders, with 95% confidence, should somewhere between
0.5447 and 0.6752. The limits also signified that views in support were higher than
views in against by 54.47% to 67.52%, indicating the practical significance of the
confidence interval limits.
10. Conclusion:
The claim in the null hypothesis was rejected, which signified that proportion of
responses of adult New Zealanders in favor of the legislation was significantly different
(greater) than that of the responses of adult New Zealanders against the legislation.

23

23
Answer 3:
a) (i) The hypothesized value of difference in productivity score was zero.
(ii) The estimated difference in productivity score (Case 1) was greater than (right hand side) the
hypothesized value at 5% level of significance. The standard deviation of the sampling
distribution (standard error) was 0.682, indicating that the estimated values of the difference
in productivity scores were not close to the hypothetical value. Hence, the hypothesized
value was observed to be outside the confidence interval of the estimated difference, which
was constructed using the standard error.
b) At 5% level of significance, all the cases excluding Case 3 demonstrated that the sample
mean difference was statistically significant.
c) (i) In Case 1 the sample mean difference was practically significant.
(ii) In Case 4 and Case 5 the sample mean differences were not practically significant.
d) In Case 2 and Case 3 sufficient evidence of practically significant mean difference was not
available. Hence, the nothing could be concluded from the confidence intervals of Case 2
and Case 3.
e) The observed mean difference in Case 6 was statistically significant at 5% level of
significance. With 95% confidence, it was inferred that the estimated mean difference of the
two payout systems would be somewhere between 0.96 hours to 5.58 hours. If the actual
difference of the means of the two pay-out systems would be as low as 0.96 hours and high
as 5.58 hours. In both cases, the results would be practically insignificant considering the
management’s decision. The model in Case 6 was statistically significant, but practically
insignificant. Statistically, Bonus pay-out system would be preferred. But, considering the
management’s consideration about the difference in productivity score the company would
like to stick to its previous model for pay-out.

23
Answer 4
a) (i) Units were 12 short stories from mystery, ironic, and literary fields.
(ii) Treatment was inclusion or exclusion of spoiler paragraph.
(iii) Response variable was the enjoyment rating of the readers.
b) (i) The graphs of the two treatments and their difference were constructed using iNZight
and have been represented in Figure 3 and Figure 4.

23
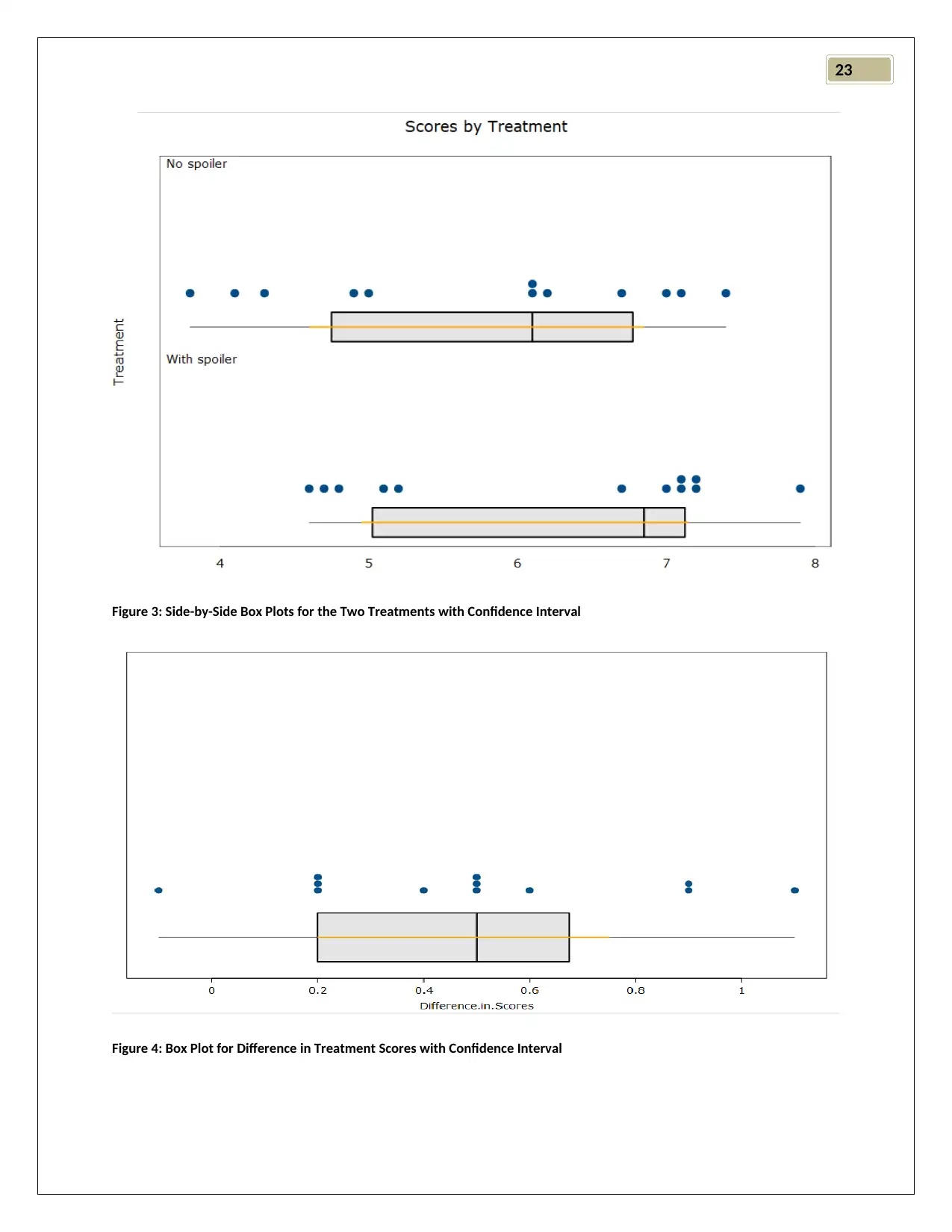
Figure 3: Side-by-Side Box Plots for the Two Treatments with Confidence Interval
Figure 4: Box Plot for Difference in Treatment Scores with Confidence Interval

23
(ii) From Figure 3 side-by-side box plots, it was evident that median of enjoyment scores
of the stories was greater in case of spoiler paragraph in front of the story. The median
enjoyment score for stories with spoiler was nearly 7.0, whereas the median score of
enjoyment for the stories without spoiler paragraph was near the 6.0 mark. With spoiler
paragraph the distribution of enjoyment scores was highly left skewed compared to that
of the scores without spoiler paragraph.
The box plot of difference in the enjoyment scores were plotted and has been represented
in Figure 4. The median of difference in enjoyment scores was around 0.5, and the
distribution was observed to follow Gaussian distribution.
c) The difference between average enjoyment scores for the two treatments was verified by
t-test as follows.
The descriptive values for both treatments have been provided in Table 2.
Table 2: Descriptive Values for Enjoyment Scores
Treatment Mean N Std.
Deviation
Std. Error
Mean
With spoiler 6.21
7 12 1.2202 .3522
No spoiler 5.72
5 12 1.2563 .3627
1. Parameter: Let μs and μns are the average enjoyment scores for stories with and without
spoiler paragraph. Hence, μs - μns denotes the difference in average enjoyment scores.
2. Null hypothesis: H0: μs - μns = 0
3. Alternate hypothesis: H1: μs - μns ¿ 0 (two-tailed)
4. Estimate: The difference in average enjoyment scores from the sample data was
x
−
s−x
−
ns=6 . 217−5 . 725=0. 4917

23
5. Test statistic: t =
( x
−
s−x
−
ns )−0
std . Error = 0 . 4917−0
0 . 1003 =4 . 900 where standard error SE = 0.1003 (from
SPSS) with 11 degrees of freedom.
6. P-value = P (|t|>0 . 4917 ) =0 . 000 (from SPSS) (Cronk, 2017)
Figure 5: Rejection Region for |t| = 4.9
7. Interpretation of P-value:
There was very strong evidence against the null hypothesis, and average enjoyment score
differences for 12 stories was found to be significantly different for two treatments.
Average enjoyment score in case of spoiler paragraph added to the story was significantly
(statistically) different (greater) than that of the stories without any spoiler paragraphs at
5% level of significance.
8. Confidence Interval:
Approximate confidence interval at 5% level of significance for μs - μns was calculated as,
CI = ( μs−μns )±t multiplier∗SE=[0 . 2708 ,0 . 7125 ] (from SPSS output).
9. Confidence Interval elucidation: With 95% probability or confidence it can be stated that
the average enjoyment score of 12 stories with spoiler would be approximately anywhere
between 0.27 less than and 0.71 more than average enjoyment score of 12 stories without
spoiler. Both hand limits of the confidence interval would be practically significant result.

23
10. Conclusion: From the sample data of 12 stories for both the treatments, very strong
evidence was found to establish significant difference in enjoyment score for reading
stories. Average enjoyment score of stories with spoiler was greater than that of stories
without spoiler. Hence, readers were enjoying reading stories with spoiler paragraph at
front.
d) The dependent variable was the difference of enjoyment scores from two treatments. The
difference scores were continuous in nature.
There were two categorical values of the treatment attribute.
From Figure 4 it was noted that no outlier values were present.
The distribution of difference of enjoyment scores seemed to be normally distributed
from Figure 4. But, using Shapiro-Wilk test in SPSS it was established that the
differences of enjoyment scores were not normally distributed (SW = 0.955, p = 0.712).
Therefore, the fourth condition for dependent t-test was not satisfied (Kim, 2015).

23
Answer 5
a) (i) Units were 1000 cyclists who completed the 180 kilometer ride event in the years
2010 to 2017.
(ii) Treatment was four age groups in the study.
(iii) Response variable was the time to complete K2.
b) (i) The graphs of the four treatments were constructed using iNZight and have been
represented in Figure 5 and Figure 6.

23
Figure 6: Distribution of Time to Complete K2 for Four Age Categories
(ii) Time taken by the cyclists to complete the event of K2 Road Cycle Classic was noted to
increase with the age of the cyclist. The median hours to complete the event increased for older
age groups. From the spread of the box plots and distribution pattern of the histograms is was
evident that due to increase in age, the variation in completion time also increased. Outliers were
also noted for each age group.
c) SPSS output for F-test has been provided in Table 3.
Table 3: ANOVA Output from SPSS
Time in hours
Sum of Squares df Mean Square F Sig.
Between Groups 64.327 3 21.442 28.104 .000
Within Groups 759.914 996 .763
Total 824.241 999

23
d) Assumptions: Event completion time of four age groups was independent of each other,
completion time for the cyclists of all the four age groups was normally distributed, and the
variances of the four age groups were significantly equal.
e) Smallest standard deviation was found for the 18-34 age group (M = 6.62, SD = 0.762) and
the highest standard deviation was found for the 55+ age group (M = 7.32, SD = 0.913). The
ratio was calculated as
0 .762
0. 913 =0. 835 .
f) The completion time of the cyclists of four age groups was independent of each other. From
Box plots of Figure 6, the symmetric nature of the distribution of completion times for the
age groups were evident. From Shapiro Wilk test the distribution of completion times for the
age groups were found to be normal (Appendix – Table 7). The assumption of homogeneity
or equality of variances for event completion time of the four age groups was found to be
true (L = 2.498, p = 0.058) (Appendix – Table 8) (Ross, & Willson, 2017).
g) (i) Null hypothesis: Variances in average event completion time for the four age groups were
equal
H0: ( σ1
2=σ2
2=σ 3
2=σ4
2 )
(ii) Alternate hypothesis: Variances in average event completion time for the four age
groups were significantly different.
(iii) Difference in average time taken by the cyclists for completion of the event were
statistically significant (F = 28.104, p < 0.05) for the four age groups at 5% level of
significance. The youngest cyclists were found to be more agile in completing the event
compared to the older age groups, and the trend was also practically significant.
h) (i) From Tukey HSD post hoc analysis difference in average completion time between the
age groups of 18-34 and 35-44 was not statistically significant (MD = - 0.336, p = 0.982) at
5% level of significance. The 95% confidence interval was found to be [-0.2665, 0.1992].
With 95% confidence, it was possible to claim that the average time (in hours) taken by the
cyclists of age group 18-34 (years) was 0.27 hours less than, and 0.20 hours greater than that
of the cyclists of 35-44 (years) age group (Murphy, Myors, & Wolach, 2014).
(ii) At 5% level statistical significance in pair wise difference of average completion time to
complete K2 was noted for the age groups of 18-34 and 45-44, 18-34 and 55+, 35-44 and
45-54, 35-44 and 55+, and 45-54 and 55+.

23
(iii) At 5% level of significance the slowest of the four age groups were the cyclists of age
group of 55+ years.
i) The cyclists took minimum of 5.45 hours and maximum of 11.29 hours to complete the K2
event. Age was a significant factor in completion time of the participants. Cyclists, aged
between 18 years to 44 years were found to complete the event with almost identical average
completion time. Cyclists, aged above 55 years were significantly slow compared to
participants of other age groups. Though, in every age group some cyclists were found to
complete the event with significant difference in completion time (outliers) (Mertler, &
Reinhart, 2016).

23
a) (i) Scenario 1: Sex and Free
Scenario 2: First and Spent
Scenario 3: Age and Purchase
Scenario 4: Quantity_Stone and Quantity_Other
Scenario 5: Shop and Spent
(ii)
Table 4: Variable Type Details
Variable Type
Sex Categorical
Age Numerical
First Categorical
Spent Numerical
Quantity_Stone Numerical
Quantity_Other Numerical
Shop Categorical
Free Categorical

23
Purchase Categorical
b) The tools that could be used for the scenarios have been provided as below.
Table 5: Tools for Different Scenarios
Scenario Tool(s)
Scenario 1
Table of counts
Side-by-side bar charts of proportions
Side-by-side stacked bar charts
Scenario 2 Side-by-side plots on the same scale
Scenario 3 Side-by-side plots on the same scale
Scenario 4
Scatter plot
Tile density plot
Scenario 5 Side-by-side plots on the same scale
c) The analyses which can be used for investigating the scenarios have been provided in the
following table.

23
Table 6: Scenario with Test Matching
Scenario Test
Scenario 1 E
Scenario 2 D
Scenario 3 F
Scenario 4 C
Scenario 5 F

23
References
Cronk, B. C. (2017). How to use SPSS®: A step-by-step guide to analysis and interpretation.
Routledge.
Hinton, P. R. (2014). Statistics explained. Routledge.
Kim, T. K. (2015). T test as a parametric statistic. Korean journal of anesthesiology, 68(6), 540-
546.
Mertler, C. A., & Reinhart, R. V. (2016). Advanced and multivariate statistical methods:
Practical application and interpretation. Routledge.
Murphy, K. R., Myors, B., & Wolach, A. (2014). Statistical power analysis: A simple and
general model for traditional and modern hypothesis tests. Routledge.
Ross, A., & Willson, V. L. (2017). One-Way Anova. In Basic and Advanced Statistical
Tests (pp. 21-24). SensePublishers, Rotterdam.

23
Appendix:
Table 7: Normality Check of the Timing of the Cyclists – SPSS Outputs
Age
Category
Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
Time in
hours
18-34 .115 142 .000 .930 142 .000
35-44 .122 271 .000 .872 271 .000
45-54 .094 408 .000 .943 408 .000
55+ .101 179 .000 .958 179 .000
a. Lilliefors Significance Correction
Table 8: Levene’s Homogeneity Test of Variances