Statistics Assignment Solution: Problems 2 and 3 - Analysis

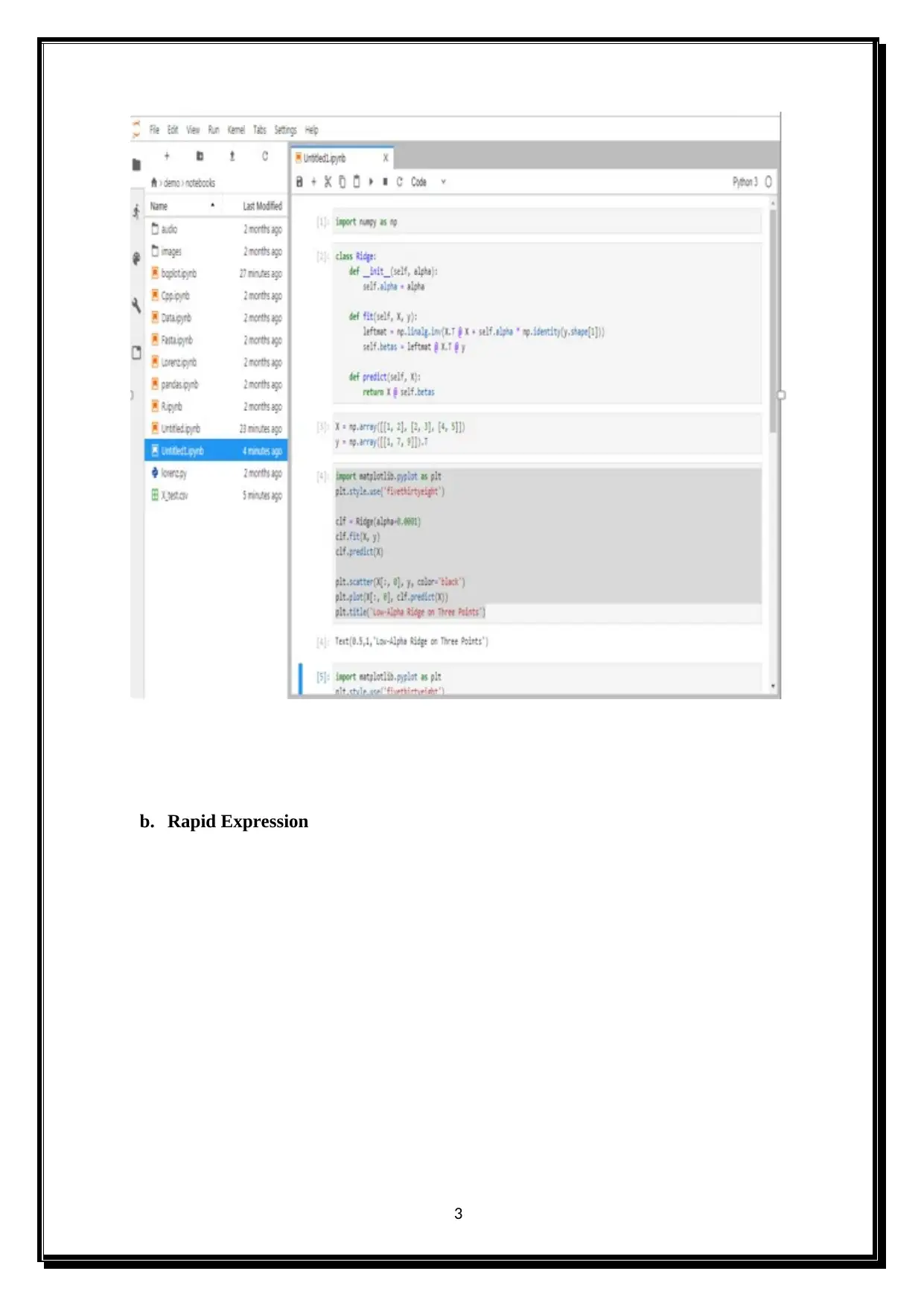
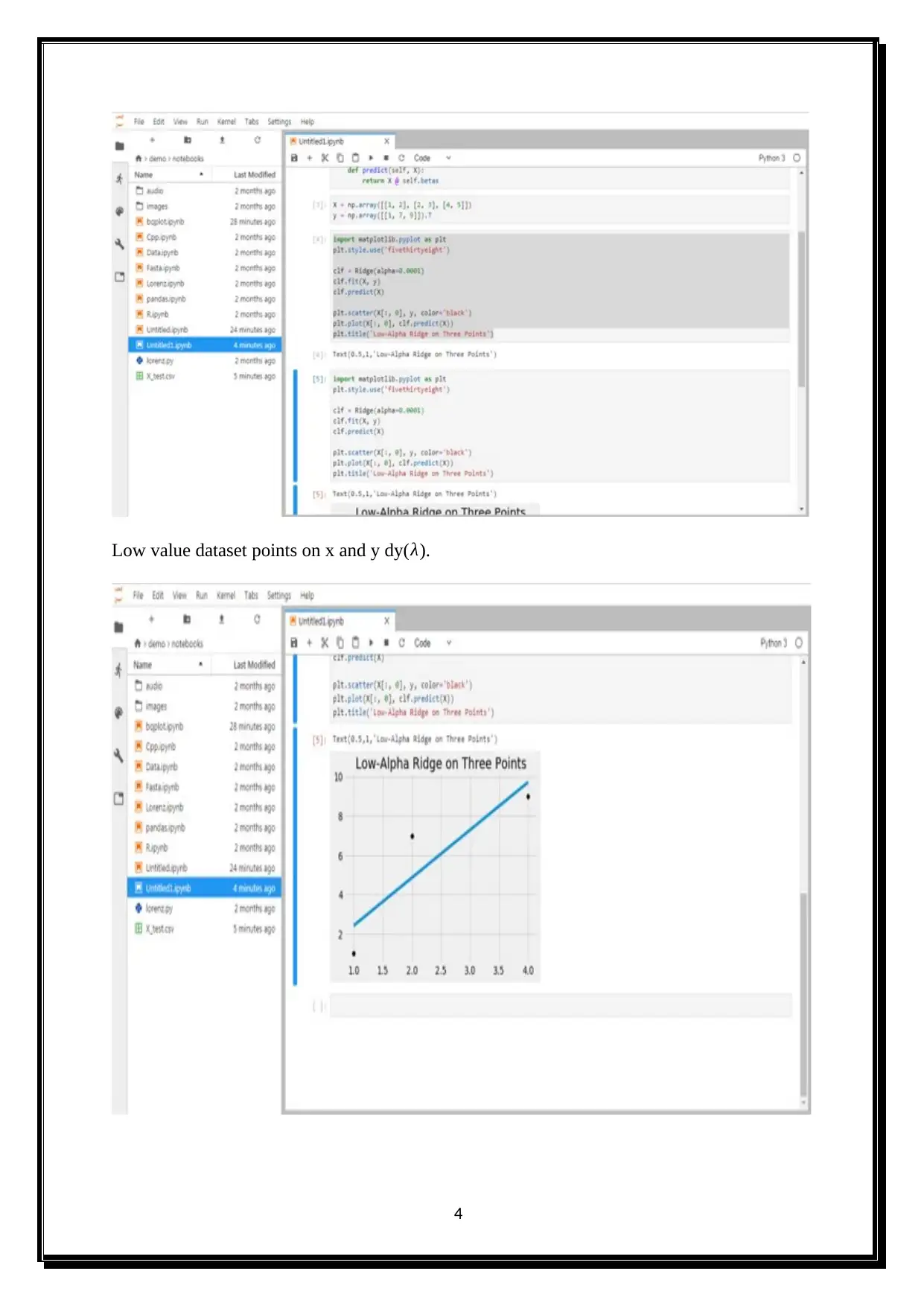
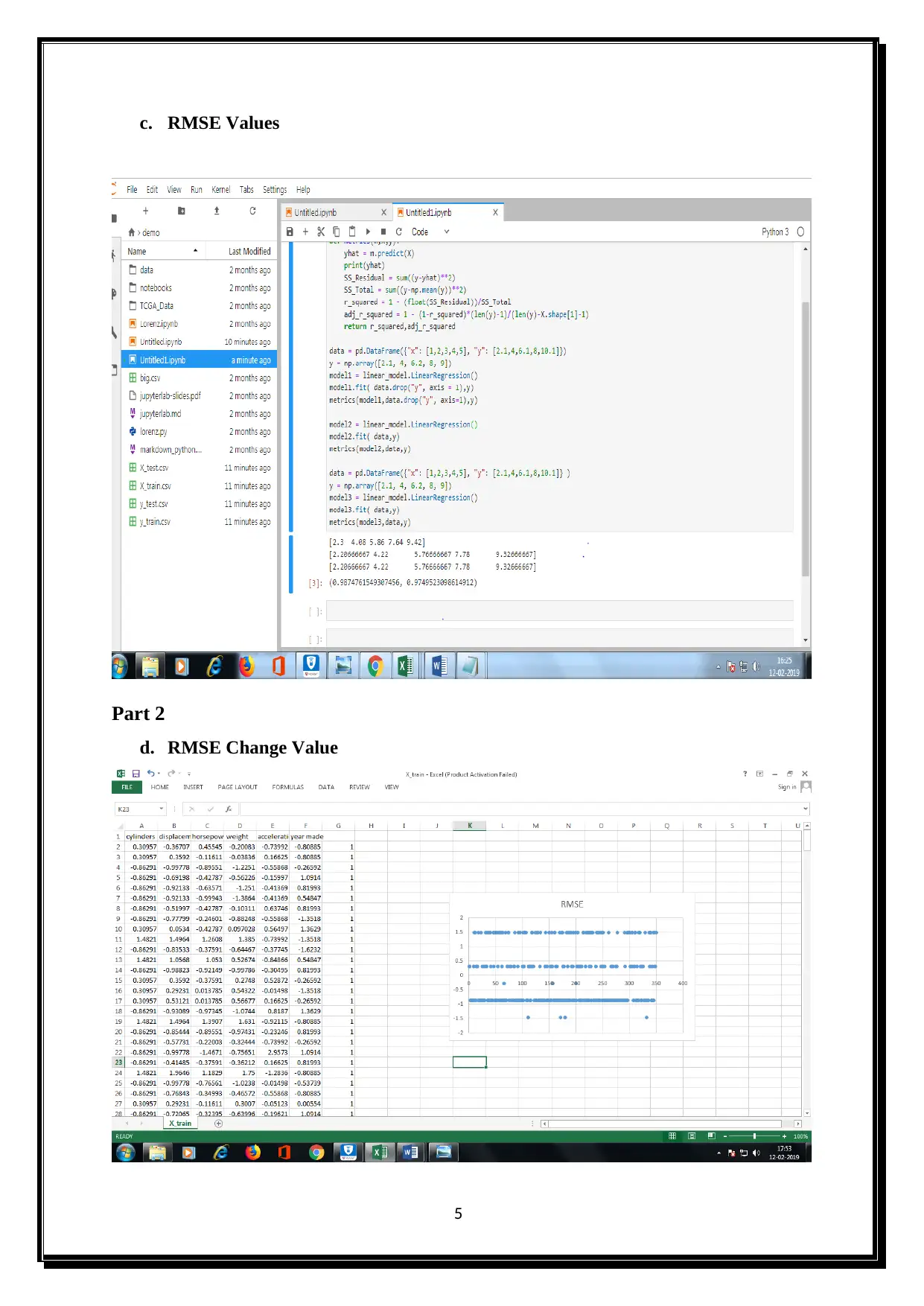
This document presents a solution to a statistics assignment, addressing problems 2 and 3. The solution to problem 2 involves applying linear regression techniques to a dataset, calculating the values of w, and minimizing errors using least squares. It includes detailed formulas and calculations for finding the intercept and vector elements within the matrix. Problem 3 is divided into two parts, with part 1 focusing on large square values, rapid expressions, low-value dataset points, and RMSE values. Part 2 addresses RMSE change values. The assignment demonstrates a practical application of statistical concepts and problem-solving skills.

Statistics
Table of Contents

Problem 2.............................................................................................................................................1
Solution.............................................................................................................................................1
Problem 3.............................................................................................................................................2
Part 1....................................................................................................................................................2
Part 2....................................................................................................................................................4

Problem 2
Solution
The initial stage of the dataset can be used for the specified range, which can access
on (x1, y1) as follows and find the problem models as,
yi ∽ iidN (xi
T w , σ 2)
It can consider the approximate data values on the dataset, which is given as,
wRR =(λI +xT x)−1 xT y
Consider the data on points f(x, y), which can be used for the regression function and find
the values of minimizing square of the sum errors, and W is the parameter.
We can consider the set of dataset(x1, y1) ...... (Xi, yi). The dataset can be used to find the
values of least square on the sum of minimization errors.
The measurement of the dataset can be used for considering the linear relationship of the
response xi, yi.
Yi=W0+∑
i=1
n
xi
T w +Si
At the same time, it can calculate the minimization of vector and values of matrices.
L=∑
i
n
∑
i=1
n
xi
T w
Xi=
x 1
x 2
… .. xn
=
The finding linear regression values can be used for the intercept and the vector elements of
the matrix values s X.
Δ wl=∑
i=1
0
¿ ¿ ¿+w)
Later, it is possible to calculate the values of w on the distribution solution i.e.,
1

E(X) = E( xT x)-1 XT y=∫(x ¿¿ T x)−1 xT ¿y)
=(x ¿¿ T x)−1 xT E[ y ]¿
= (x ¿¿ T x)−1 ¿ xT X [w ]
= w
Var [y]=E [[y-E(y))(y-E[y])T]=∑ w
Let us consider the assumption values and display the Gaussian values, which are as follows,
E[wml]=w, var [wml]=σ 2(XT X)-1
The finding values is E( wRR)=0.05.
The finding values is V(wRR)=0.10.
Problem 3
Part 1
a. Large Square Value
2

b. Rapid Expression
3

Low value dataset points on x and y dy( λ).
4

c. RMSE Values
Part 2
d. RMSE Change Value
5