Comprehensive STEM Assignment: Applying Maths & Science Principles
VerifiedAdded on 2023/04/08
|10
|1331
|97
Homework Assignment
AI Summary
This document presents a comprehensive solution to a STEM assignment, covering a range of topics from dimensional analysis and geometric series to radioactive decay and statistical analysis. The solutions demonstrate the application of mathematical and scientific principles to solve problems in physics, statistics, and electrical engineering. Topics include determining dimensions of physical quantities, analyzing geometric series, calculating radioactive decay rates, and applying statistical distributions. Furthermore, trigonometric problems, vector analysis, and electrical circuit analysis are addressed, providing detailed step-by-step solutions and explanations. The assignment leverages various formulas and concepts to arrive at accurate and well-supported answers. Desklib offers a wide array of similar solved assignments and past papers for students seeking additional learning resources.

LO1
a) Dimension of p = kg/m/sec = ML-1T
Dimension of rho = ML-3
Dimension of volume = L3
Dimension of velocity = LT-1
L T−1 =¿
Equating x, y and z
x + y=0=¿ y=1
−x−3 y +3 z=1=¿1−3+3 z=1=¿ z=1
x=−1
b) Coefficient of viscosity = ML-1T-1
Dimension of velocity = LT-1
Dimension of Radius = L
M 1 L1 T−2=¿
Equating x, y and z,
x=1
−x + y + z=1=¿ z=1
−x− y =−2=¿ y =1
F=η V R
(MIT, 2019)
c) 8
2 ( 2 ×3+7 × d ) =2 × 5
2 ( 2 ×3+ 4 × d )
4 ( 6+7 d )=5 ( 6 +4 d )
24+ 28 d=30+20 d
d= 3
4
Sum of the geometric series,
S= a (rn−1)
(r −1) =8 ¿ ¿
d) d= h
tan20 − h
tan 60
d= h
tan20 − h
tan 60
a) Dimension of p = kg/m/sec = ML-1T
Dimension of rho = ML-3
Dimension of volume = L3
Dimension of velocity = LT-1
L T−1 =¿
Equating x, y and z
x + y=0=¿ y=1
−x−3 y +3 z=1=¿1−3+3 z=1=¿ z=1
x=−1
b) Coefficient of viscosity = ML-1T-1
Dimension of velocity = LT-1
Dimension of Radius = L
M 1 L1 T−2=¿
Equating x, y and z,
x=1
−x + y + z=1=¿ z=1
−x− y =−2=¿ y =1
F=η V R
(MIT, 2019)
c) 8
2 ( 2 ×3+7 × d ) =2 × 5
2 ( 2 ×3+ 4 × d )
4 ( 6+7 d )=5 ( 6 +4 d )
24+ 28 d=30+20 d
d= 3
4
Sum of the geometric series,
S= a (rn−1)
(r −1) =8 ¿ ¿
d) d= h
tan20 − h
tan 60
d= h
tan20 − h
tan 60
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
h
tan 20 − h
tan 60 /( 1
60 )=600
h
tan 20 − h
tan 60 =10
h=4.61 miles
e) 2) Radioactive decay equation
dN
dt =−λ N
dN
N =−λ dt
N=N 0 e−λt
Half-life is defined as,
t0.5= ln 2
λ
And half-life is given to be 1 week, so λ
λ=0.693/week
3) N=N 0 e−λt
N=20 e−0.693× 3
N=20× 0.125=2.5
After three weeks it will be 2.5 counts per second.
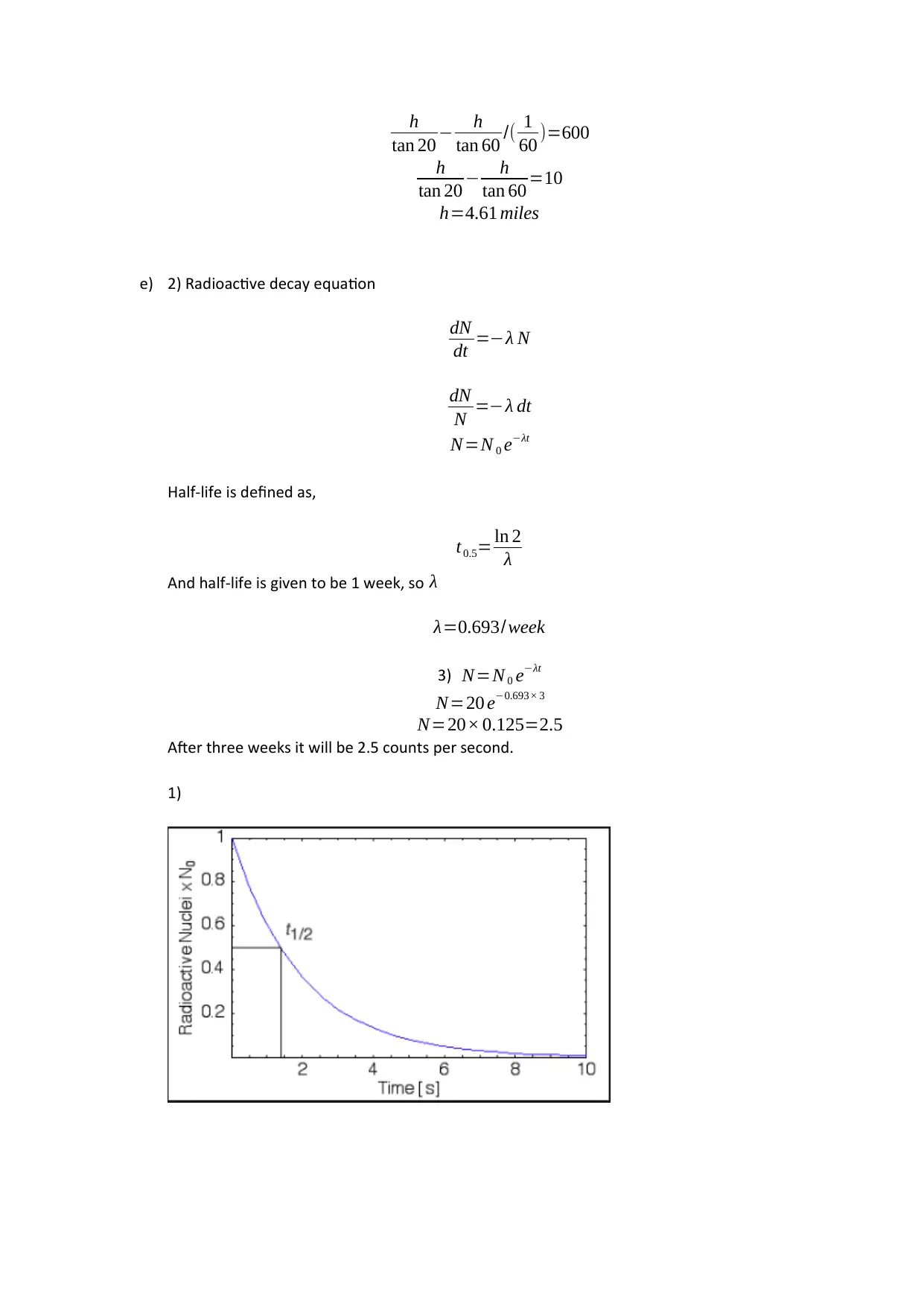
1)
tan 20 − h
tan 60 /( 1
60 )=600
h
tan 20 − h
tan 60 =10
h=4.61 miles
e) 2) Radioactive decay equation
dN
dt =−λ N
dN
N =−λ dt
N=N 0 e−λt
Half-life is defined as,
t0.5= ln 2
λ
And half-life is given to be 1 week, so λ
λ=0.693/week
3) N=N 0 e−λt
N=20 e−0.693× 3
N=20× 0.125=2.5
After three weeks it will be 2.5 counts per second.
1)

f) 1) Since it is an exponential in nature
N=N 0 eλt
From the data we can estimate λ=0.255
2) In 2025, t =25 years
N2025=225 e0.255× 25
N2025=132071.7
3)
N2010=225 e0.255× 10
N2010=2881.59
Average rate of change from 2006 to 2010 is,
(N ¿¿ 2010−N2006)/4 ¿
Rate of change=461.15
4) Instantaneous change is = 0.255 * 225 = 57.375
LO2
a) Mean = 49.2
Standard deviation = 16.12328
b) If x is a random variable with distribution B(n, p), then for sufficiently large n, the following
random variable has a standard normal distribution:
z= x−μ
σ N ( 0,1 ) , μ=np , σ 2=np(1− p)
Proof:
N=N 0 eλt
From the data we can estimate λ=0.255
2) In 2025, t =25 years
N2025=225 e0.255× 25
N2025=132071.7
3)
N2010=225 e0.255× 10
N2010=2881.59
Average rate of change from 2006 to 2010 is,
(N ¿¿ 2010−N2006)/4 ¿
Rate of change=461.15
4) Instantaneous change is = 0.255 * 225 = 57.375
LO2
a) Mean = 49.2
Standard deviation = 16.12328
b) If x is a random variable with distribution B(n, p), then for sufficiently large n, the following
random variable has a standard normal distribution:
z= x−μ
σ N ( 0,1 ) , μ=np , σ 2=np(1− p)
Proof:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

By the linear transformation of the moment generating function,
Taking log on both sides
Using the log expansion and collecting the terms of θ
σ
Taking limit where n tends to infinity we get,
Which is the moment generating function of a standard normal distribution. (Mehra2, Vol.
12, 2017)
c) P ( X −μ
σ )=0.97
Taking log on both sides
Using the log expansion and collecting the terms of θ
σ
Taking limit where n tends to infinity we get,
Which is the moment generating function of a standard normal distribution. (Mehra2, Vol.
12, 2017)
c) P ( X −μ
σ )=0.97
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

( X −10
2 )=1.89
X =10+3.78=13.78
d) 1) P (Rejected) =0.12
P (X ≤2) = P (X=0) + P (X=1) + P (X=2)
P ( X ≤2 ) =10C0
( 0.12 )0 ( 0.88 )10 +10C1
( 0.12 )1 ( 0.88 )9+10C2
( 0.12 )2 ( 0.88 )8 =0.891
2) 1 – (P (X=0) + P (X=1)) = 1 – {10C0
( 0.12 )0 ( 0.88 )10+10C1
( 0.12 )1 ( 0.88 )9 } = 0.341
3) In the first case it is profitable and in the second case it is a loss
e) Standardised normal scores for 1250 = 1250−1000
125 =2
Standardised normal scores for 1250 = 980−1000
125 =−0.16
Standardised normal scores for 1250 = 1150−1000
125 =1.2
LO3
a) 1) Maximum value = 20 , Minimum value = 4
a+c=20
−a+c=4
a=8 , c=12
period is365 so , 365= 2 π
b
b= 2 π
365
t = 31 + 28 + 31 + 30 + 31 + 21 = 172 (number of days from January 1st to 21 st of June)
Therefore the horizontal shift (translation) of 172 is to the right and d = 172.
2) P ( t ) =8 cos( ¿ 2 π
365 (t−172))+12 ¿
2 )=1.89
X =10+3.78=13.78
d) 1) P (Rejected) =0.12
P (X ≤2) = P (X=0) + P (X=1) + P (X=2)
P ( X ≤2 ) =10C0
( 0.12 )0 ( 0.88 )10 +10C1
( 0.12 )1 ( 0.88 )9+10C2
( 0.12 )2 ( 0.88 )8 =0.891
2) 1 – (P (X=0) + P (X=1)) = 1 – {10C0
( 0.12 )0 ( 0.88 )10+10C1
( 0.12 )1 ( 0.88 )9 } = 0.341
3) In the first case it is profitable and in the second case it is a loss
e) Standardised normal scores for 1250 = 1250−1000
125 =2
Standardised normal scores for 1250 = 980−1000
125 =−0.16
Standardised normal scores for 1250 = 1150−1000
125 =1.2
LO3
a) 1) Maximum value = 20 , Minimum value = 4
a+c=20
−a+c=4
a=8 , c=12
period is365 so , 365= 2 π
b
b= 2 π
365
t = 31 + 28 + 31 + 30 + 31 + 21 = 172 (number of days from January 1st to 21 st of June)
Therefore the horizontal shift (translation) of 172 is to the right and d = 172.
2) P ( t ) =8 cos( ¿ 2 π
365 (t−172))+12 ¿
3)
8 cos (¿ 2 π
365 (t−172))+12=4 ¿
cos (¿ 2 π
365 (t−172))=−1 ¿
2 π
365 ( t −172 )=π
t=354.5
Day is mid of 20th December where minimum occurs
4 8 cos (¿ 2 π
365 (t−172))+12=16 ¿
cos (¿ 2 π
365 (t−172))=0.5 ¿
2 π
365 ( t−172 )=± π
3 , ± 5 π
3
Only once it happens.
b)
8 cos (¿ 2 π
365 (t−172))+12=4 ¿
cos (¿ 2 π
365 (t−172))=−1 ¿
2 π
365 ( t −172 )=π
t=354.5
Day is mid of 20th December where minimum occurs
4 8 cos (¿ 2 π
365 (t−172))+12=16 ¿
cos (¿ 2 π
365 (t−172))=0.5 ¿
2 π
365 ( t−172 )=± π
3 , ± 5 π
3
Only once it happens.
b)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

T 1=T 1× −1
√2⃑ i+T 1× 1
√2⃑ j
T 2=T 2 × √3
2⃑ i+T 2× 1
2⃑ j
c) Angle between the two vectors = 105 degrees
Resultant force = √202 +302 +2 ( 20 ) ( 30 ) cos 105 °
R=31.455lb
d)⃑
P .⃑ Q=|P|∨Q∨cos θ⃑
P .⃑ Q=13
|P|=8.062
|Q|=3.605
cos θ=63.43 °
e) & f)
The first thing is that the question given
cos (x+ π
x ) should be replaced with cos (x + π
2 )
As,
cos ( x+ π
x ) ≠ sin(x−π )≠ sin ( x+ π )
So working with cos (x+ π
2 ), sin ( x−π )∧sin (x+ π )
sin ( x−π ) =sin ( − ( π −x ) ) =−sin ( π− x ) =−sin x
sin ( x +π )=−sin x
cos ( x+ π
2 ) =−sin x
So all are same
sin ( x−π )=sin x cos π−cos x sin π=−sin x
sin ( x +π )=sin x cos π + cos x sin π=−sin x
cos (x+ π
2 )=cos x cos π
2 −sin x sin π
2 =0−sin x sin π
2 =−sin x
Considering x = π
3 degrees
√2⃑ i+T 1× 1
√2⃑ j
T 2=T 2 × √3
2⃑ i+T 2× 1
2⃑ j
c) Angle between the two vectors = 105 degrees
Resultant force = √202 +302 +2 ( 20 ) ( 30 ) cos 105 °
R=31.455lb
d)⃑
P .⃑ Q=|P|∨Q∨cos θ⃑
P .⃑ Q=13
|P|=8.062
|Q|=3.605
cos θ=63.43 °
e) & f)
The first thing is that the question given
cos (x+ π
x ) should be replaced with cos (x + π
2 )
As,
cos ( x+ π
x ) ≠ sin(x−π )≠ sin ( x+ π )
So working with cos (x+ π
2 ), sin ( x−π )∧sin (x+ π )
sin ( x−π ) =sin ( − ( π −x ) ) =−sin ( π− x ) =−sin x
sin ( x +π )=−sin x
cos ( x+ π
2 ) =−sin x
So all are same
sin ( x−π )=sin x cos π−cos x sin π=−sin x
sin ( x +π )=sin x cos π + cos x sin π=−sin x
cos (x+ π
2 )=cos x cos π
2 −sin x sin π
2 =0−sin x sin π
2 =−sin x
Considering x = π
3 degrees
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

sin ( π
3 −π )=sin ¿ ¿
sin ( π
3 + π )=sin ¿ ¿
cos ( π
3 + π
2 )=cos 5 π
6 =cos (π − π
6 )=−cos π
6 =¿− √3
2 ¿
Therefore it is analytically proven also
(Trigonometry, 2019)
g)
sin ( a+ b ) =sin a cos b+cos a sin b= 3
5 × ( −12
13 ) + ( −4
5 ) × ( 5
13 ) =−56
65
LO4
a)
dR
dt × −1
R2 = d R1
dt × −1
R1
2
dR
dt = ( d R1
dt × 1
R1
2 ) × R2
dR
dt = ( d R1
dt × 1
R1
2 ) × ( 1
R1
+ 1
R2 )
2
b) Distance travelled∈3 minute=v ( 3 )−v ( 2 )= (1+12+27 )− ( 1+8+12 ) =19
c) 1)
longitudinal stress= F
A = 40
2× π × r × h = 40
2× π × 0.0005× 3 = 40
9.425× 10−3 =4244.132 N /m2
2)
longitudinal strain= longitudinal stress
Y
longitudinal strain=2.02×10−8
3)
3 −π )=sin ¿ ¿
sin ( π
3 + π )=sin ¿ ¿
cos ( π
3 + π
2 )=cos 5 π
6 =cos (π − π
6 )=−cos π
6 =¿− √3
2 ¿
Therefore it is analytically proven also
(Trigonometry, 2019)
g)
sin ( a+ b ) =sin a cos b+cos a sin b= 3
5 × ( −12
13 ) + ( −4
5 ) × ( 5
13 ) =−56
65
LO4
a)
dR
dt × −1
R2 = d R1
dt × −1
R1
2
dR
dt = ( d R1
dt × 1
R1
2 ) × R2
dR
dt = ( d R1
dt × 1
R1
2 ) × ( 1
R1
+ 1
R2 )
2
b) Distance travelled∈3 minute=v ( 3 )−v ( 2 )= (1+12+27 )− ( 1+8+12 ) =19
c) 1)
longitudinal stress= F
A = 40
2× π × r × h = 40
2× π × 0.0005× 3 = 40
9.425× 10−3 =4244.132 N /m2
2)
longitudinal strain= longitudinal stress
Y
longitudinal strain=2.02×10−8
3)

longitudinal strain= ∆ l
L
∆ l=6.06 ×10−8
d) 1)
V l=4 di
dt
Instantaneous Current,
I l= V s
R (1−e
−Rt
L )
putting the values Il =100
20 ( 1−e
−20 t
4 ) =5 ( 1−e−5 t )
dI
dt =25 e−5t
V l=100 e−5 t
2) After the switch is transferred to position 2 then the inductor acts as a wire and there will
be no voltage drop and the current will be putting infinity in the value of current
V l=0∧I l=5
3) dI
dt =25 e−5t
At t=0,
dI
dt =25
(Electrical, 2019)
e)
y=x3−6 x2 +9 x
Stationary points can be obtained by differentiating with respect to x
dy
dx =3 x2 −12 x +9=0
L
∆ l=6.06 ×10−8
d) 1)
V l=4 di
dt
Instantaneous Current,
I l= V s
R (1−e
−Rt
L )
putting the values Il =100
20 ( 1−e
−20 t
4 ) =5 ( 1−e−5 t )
dI
dt =25 e−5t
V l=100 e−5 t
2) After the switch is transferred to position 2 then the inductor acts as a wire and there will
be no voltage drop and the current will be putting infinity in the value of current
V l=0∧I l=5
3) dI
dt =25 e−5t
At t=0,
dI
dt =25
(Electrical, 2019)
e)
y=x3−6 x2 +9 x
Stationary points can be obtained by differentiating with respect to x
dy
dx =3 x2 −12 x +9=0
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

x2−4 x+3= ( x−1 ) ( x−3 ) =0 , x=1∨3
So stationary points are 1 and 3
d2 y
dx2 =6 x−12
At x = 1,
d2 y
dx2 =−6
So X=1 is the maximum point
At x =3,
d2 y
dx2 =6
So X=3 is minimum point
Bibliography
Electrical. (2019). LR Series Circuit. Retrieved from Electronics Tutorials: https://www.electronics-
tutorials.ws/inductor/lr-circuits.html
Mehra2, S. B. ( Vol. 12, 2017). Convergence of Binomial to Normal:Multiple Proofs. International
Mathematical Forum, 399 - 411. Retrieved from http://www.m-hikari.com/imf/imf-2017/9-
12-2017/p/baguiIMF9-12-2017.pdf
MIT. (2019). Dimensions of Commonly Encountered Quantities. Retrieved from Chapter 2 Units,
Dimensional Analysis, Problem Solving, and:
http://web.mit.edu/8.01t/www/materials/modules/chapter02.pdf
Trigonometry. (2019). Trigonometric ratios of compound angles. Retrieved from TRIGONOMETRIC
RATIOS OF COMPOUND ANGLES: https://www.onlinemath4all.com/compound-angles.html
So stationary points are 1 and 3
d2 y
dx2 =6 x−12
At x = 1,
d2 y
dx2 =−6
So X=1 is the maximum point
At x =3,
d2 y
dx2 =6
So X=3 is minimum point
Bibliography
Electrical. (2019). LR Series Circuit. Retrieved from Electronics Tutorials: https://www.electronics-
tutorials.ws/inductor/lr-circuits.html
Mehra2, S. B. ( Vol. 12, 2017). Convergence of Binomial to Normal:Multiple Proofs. International
Mathematical Forum, 399 - 411. Retrieved from http://www.m-hikari.com/imf/imf-2017/9-
12-2017/p/baguiIMF9-12-2017.pdf
MIT. (2019). Dimensions of Commonly Encountered Quantities. Retrieved from Chapter 2 Units,
Dimensional Analysis, Problem Solving, and:
http://web.mit.edu/8.01t/www/materials/modules/chapter02.pdf
Trigonometry. (2019). Trigonometric ratios of compound angles. Retrieved from TRIGONOMETRIC
RATIOS OF COMPOUND ANGLES: https://www.onlinemath4all.com/compound-angles.html
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
