Stock Price Analysis: British Petroleum P.L.C. (2018) - Module X

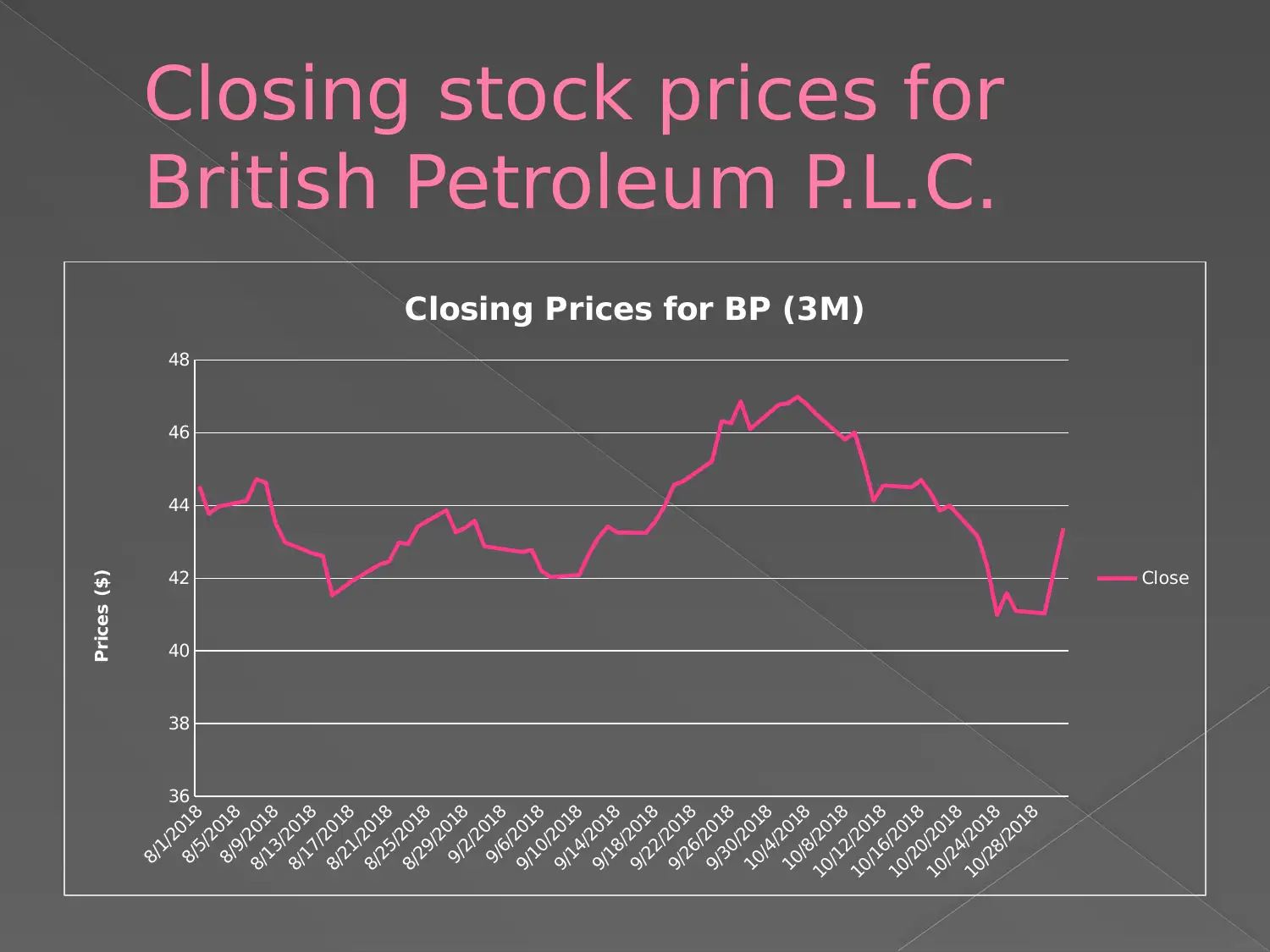
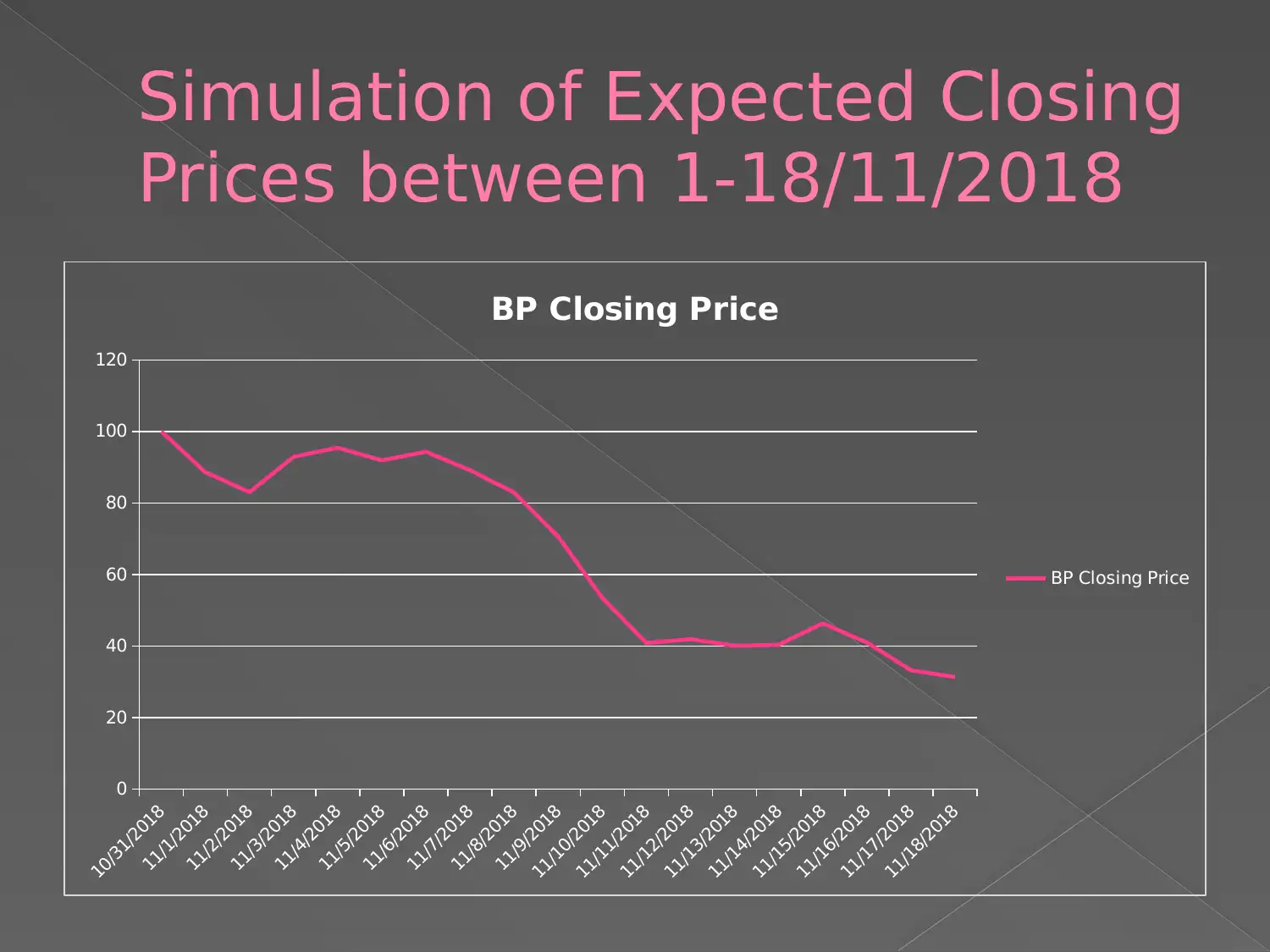
This report presents an analysis of British Petroleum's (BP) stock prices, focusing on the application of Geometric Brownian Motion (GBM). The report discusses the concepts of drift (Mu) and volatility (Sigma) and their relationship to time, emphasizing that these parameters are not constant. The report explains the significance of a small standard deviation in share prices, indicating market stability, which is a prerequisite for GBM models. The analysis covers a time frame of less than two years, meeting the conditions for GBM. The report references relevant literature and includes appendices. The primary focus is to analyze the behavior of the share prices of British Petroleum and to apply a financial model to it.

THE BEHAVIOR AND PERFORMANCE OF
SHARE PRICES
Assessment Task 2

The meaning of Mu and
Sigma
 In the equation, Mu is called the drift at
time t, and Sigma the diffusion
(volatility) at time t for a given stock. No
they are not constant since their
respective values are dependent on time
i.e. t=0, 1, 2.
 This means that the values of drift and
volatility change with variation in time. If
they were constant they would be
represented in the form and .

Closing stock prices for
British Petroleum P.L.C.
8/1/2018
8/5/2018
8/9/2018
8/13/2018
8/17/2018
8/21/2018
8/25/2018
8/29/2018
9/2/2018
9/6/2018
9/10/2018
9/14/2018
9/18/2018
9/22/2018
9/26/2018
9/30/2018
10/4/2018
10/8/2018
10/12/2018
10/16/2018
10/20/2018
10/24/2018
10/28/2018
36
38
40
42
44
46
48
Closing Prices for BP (3M)
Close
Prices ($)

Geometric Brownian Motion
 The standard deviation of the share prices should be
considerably small or equivalent to t . This will indicate that the
market is stable because Geometric Brownian Motion models
are only applicable in a stable market. Second we will evaluate
the duration over which the share prices were collected i.e.
should be less than 2 years and preferably 3 to 6 months. From
the results below it is clear that our share prices satisfy the
necessary Geometric Brownian Motion conditions (Dmouj 2006).
Standard Deviation 1.579365
Duration in days 65

Computing Mu and Sigma

Simulation of Expected Closing
Prices between 1-18/11/2018
10/31/2018
11/1/2018
11/2/2018
11/3/2018
11/4/2018
11/5/2018
11/6/2018
11/7/2018
11/8/2018
11/9/2018
11/10/2018
11/11/2018
11/12/2018
11/13/2018
11/14/2018
11/15/2018
11/16/2018
11/17/2018
11/18/2018
0
20
40
60
80
100
120
BP Closing Price
BP Closing Price

References
 Dmouj, A (2006), Stock price
modelling:Theory and Practice,
Master's Thesis, Faculty of sciences,
Vrije Universiteit, Vrije Universiteit
Press, Amsterdam.
 Gheorghiu, V. (2011), Ito calculus in a
nutshell, Academic, Department of
Physics, Carnegie Mellon University,
CMU, Pittsburgh.

Appendices