Structural Analysis 1 Assignment: Truss Force & Beam Deflection Calc

This assignment solution covers fundamental concepts in structural analysis, focusing on determining forces in truss members and calculating deflections in beams. The first question involves analyzing a truss structure to find the forces in each member, identifying whether they are in tension or compression, using methods of joints. The second question deals with calculating the deflection of a beam under given loading conditions, including uniformly distributed loads and point loads. The solution utilizes integration methods to derive the deflection equation, considering boundary conditions to determine constants of integration. Numerical results for deflection at specific points, such as the midspan and free ends, are calculated and presented. This document is available on Desklib, a platform that provides students with access to past papers and solved assignments.

Structural Analysis 1
STRUCURAL ANALYSIS
Name:
Class:
Professor:
School:
City:
Date:

Structural Analysis 2
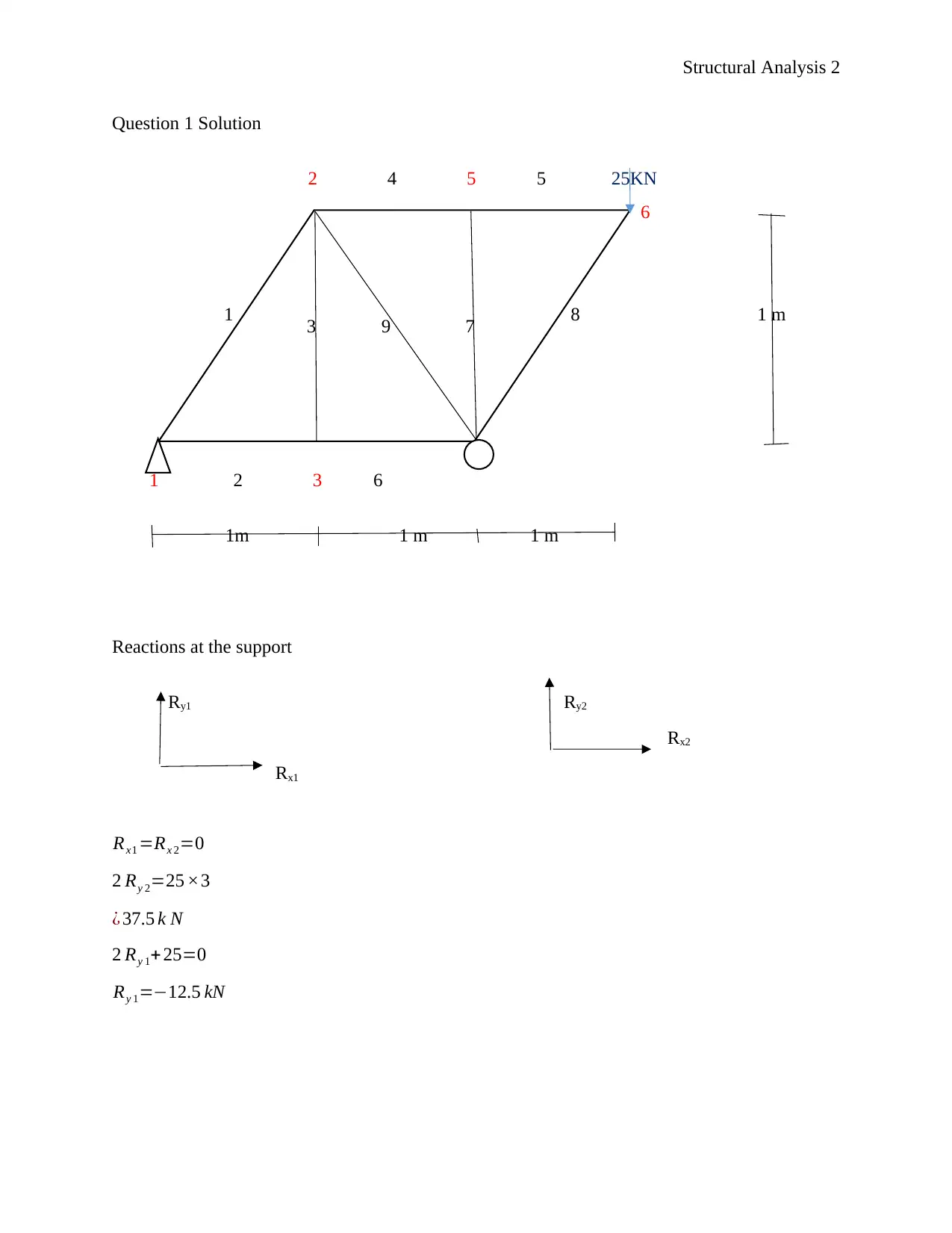
Question 1 Solution
2 4 5 5 25KN
6
1 8 1 m
1 2 3 6
1m 1 m 1 m
Reactions at the support
Ry1 Ry2
Rx2
Rx1
Rx1 =Rx 2=0
2 Ry 2=25 ×3
¿ 37.5 k N
2 Ry 1+ 25=0
Ry 1=−12.5 kN
3 9 7

Structural Analysis 3
Node 1
√2
1 m
1 m
F1
F2
12kN
∑ H =0
F2+ 1
√ 2 F1 =0
∑ V =0
12.5− 1
√ 2 F1=0
F1=12.5 √2 kN =17.68 kN (Tension)
F2+ 1
√ 2 ( 12.5 √2 )=0
F2+ 1
√ 2 ( 12.5 √2 )=0
F2=−12.5 kN =12.5 kN (Compression)
Hence , F6 =F2=−12.5 kN=12.5 kN ( Compression )
Node 3

Structural Analysis 4
F4
F1 F3 F9
F3=F7 =0
∑ H =0
F4 + 1
√2 F9− 1
√2 F1=0
F4 + 1
√2 F9− 1
√2 ( 12.5 √2 )=0
F4 + 1
√2 F9−12.5=0
∑ V =0
1
√2 F1 + 1
√2 F9=0
1
√2 ( 12.5 √2 ) + 1
√2 F9=0
F9=−12.5 √ 2=17.68 kN (Compression)
Therefore , F4 + 1
√ 2 (−12.5 √2 )−12.5=25 kN ( Tension )
Node 6
25 kN
F5
F8
∑ H =0
F5+ 1
√ 2 F8=0

Structural Analysis 5
∑ V =0
25+ 1
√ 2 F8 =0
F8=−25 √ 2 kN=35.36 kN (Compression)
F5+ 1
√ 2 (−25 √2 )=0
F5=25 kN ( Tension )
F1=12.5 √ 2 kN =17.68 kN (Tension)
F2=12.5 kN (Compression)
F3=0
F4=25 kN (Tension )
F5=25 kN ( Tension )
F6=12.5 kN (Compression)
F7=0
F8=35.36 kN (Compression)
F9=17.68 kN (Compression)
Question 2 Solution
2kN UDL=5kN/m 2kN
2m 8m 2m
x
EI =43 ×1012 N ∙mm2=43 ×103 kN ∙ m2
E I y' ' =M
Moments about R1=0 , hence

Structural Analysis 6
8 R2= (2 ×10 )+ ( 5× 10× 5 )− (2 ×2 )− ( 2× 2× 1 )
R2=32 kN
R1= (12 ×5 )+ ( 4 )−32=32 kN
E I y' ' =2 x +5 x2
2 −32 ( x−2 ) +5 ( x−10 ) 2
2 −32 ( x−10 ) +5 ( x−10 ) 2
2
Integrate bothsides of the equation
E I ∫ ( y' ' ) =∫ ( 2 x +5 x2
2 −32 ( x−2 ) +5 ( x−2 )2
2 −32 ( x−10 ) +5 ( x −2 ) 2
2 )
E I y'=x2 + 5 x3
6 −16 ( x−2 ) 2 + 5 ( x−2 ) 3
6 −16 ( x−10 ) 2+ 5 ( x−10 ) 3
6 +C1
Integrate bothsides of the equation
E I ∫ ( y' )=∫ ( x2 + 5 x3
6 −16 ( x−2 ) 2+ 5 ( x−2 ) 3
6 −16 ( x−10 ) 2 + 5 ( x−10 ) 3
6 +C1 )
E I y = x3
3 + 5 x4
24 −16 ( x−2 ) 3
3 + 5 ( x −2 ) 4
24 − 16 ( x−10 ) 3
3 + 5 ( x−10 ) 4
24 +C1 x +C2
At x=2 , y =0 , hence
23
3 + 5(2)4
24 − 16 ( 2−2 ) 3
3 + 5 ( 2−2 ) 4
24 −16 ( 2−10 ) 3
3 + 5 ( 2−10 ) 4
24 +2 C1 +C2=0
8
3 + 10
3 + 8192
3 − 2560
3 +2C1 +C2 =0
5650
3 +2 C1+C2=0 (i)
At x=10 , y =0 , hence
103
3 + 5(10)4
24 − 16 ( 10−2 )3
3 + 5 ( 10−2 ) 4
24 − 16 ( 10−10 )3
3 + 5 ( 10−10 ) 4
24 +10 C1 +C2=0
1000
3 + 6250
3 − 8192
3 + 2560
3 +10 C1+C2=0
1618
3 +10 C1 +C2=0(ii)
Solving (i ) ∧ ( ii ) simultaneously ,

Structural Analysis 7
5650
3 +2 C1+C2=0
−¿
1618
3 +10 C1 +C2=0
4032
3 −8 C1=0
C1=504
3 =168
1618
3 + 504 0
3 +C2=0
C2=−6658
3
Therefore ,
EIy= x3
3 + 5 x4
24 −16 ( x−2 )3
3 + 5 ( x−2 )4
24 −16 ( x−10 )3
3 + 5 ( x −10 )4
24 + 504
3 x− 6658
3
Deflection at midspan , x=6
EIy= 63
3 + 5 ( 6 ) 4
24 − 16 ( 6−2 )3
3 + 5 ( 6−2 ) 4
24 − 16 ( 6−10 ) 3
3 + 5 ( 6−10 ) 4
24 + 504 ( 6 )
3 − 6658
3
EIy= 18
3 + 810
3 −1024
3 + 160
3 −1024
3 + 160
3 + 3024
3 − 6658
3
EIy=−4534
3
But EI=43 ×103 kN ∙ m2 , hence
y= −4534
3 ( 43 × 103 ) =−0.03515 m=35.15 mm
Deflectioat free ends , x=0∧x=12
EIy= 03
3 + 5 ( 0 ) 4
24 − 16 ( 0−2 ) 3
3 + 5 ( 0−2 ) 4
24 − 16 ( 0−10 ) 3
3 + 5 ( 0−10 ) 4
24 + 504 ( 0 )
3 −6658
3
EIy= 128
3 + 10
3 + 16000
3 + 6250
3 − 6658
3 =15730
3

Structural Analysis 8
But EI=43 ×103 kN ∙ m2 , hence
y= 15730
3 ( 43 × 103 ) =0.1219 m=121.9 mm
EIy= 123
3 + 5 ( 12 ) 4
24 − 16 ( 12−2 ) 3
3 + 5 ( 12−2 ) 4
24 −16 ( 12−10 ) 3
3 + 5 ( 12−10 ) 4
24 + 504 ( 12 )
3 − 6658
3
EIy= 1728
3 + 12960
3 − 16000
3 + 6250
3 − 128
3 + 10
3 + 6048
3 −6658
3 = 4210
3
But EI=43 ×103 kN ∙ m2 , hence
y= 4210
3 ( 43 × 103 ) =0.03264 m=32.64 mm
Question 2 Solution
RA 3kN/m P1=1kN RB P2=2kN
A C D B E
HA
5/3 m 2.5/3 m
2.5 m 1 m 1.5 m 5 m
Area of trapezoidal load= 1
2 × 3× 2.5=3.75 kN
5 RB = ( 2 ×10 ) + ( 3.5 ×1 ) + (3.75× 5
3 )
RB=5.95 kN
RA =2+1+3.75−5.95
RB=0.8 kN

Structural Analysis 9
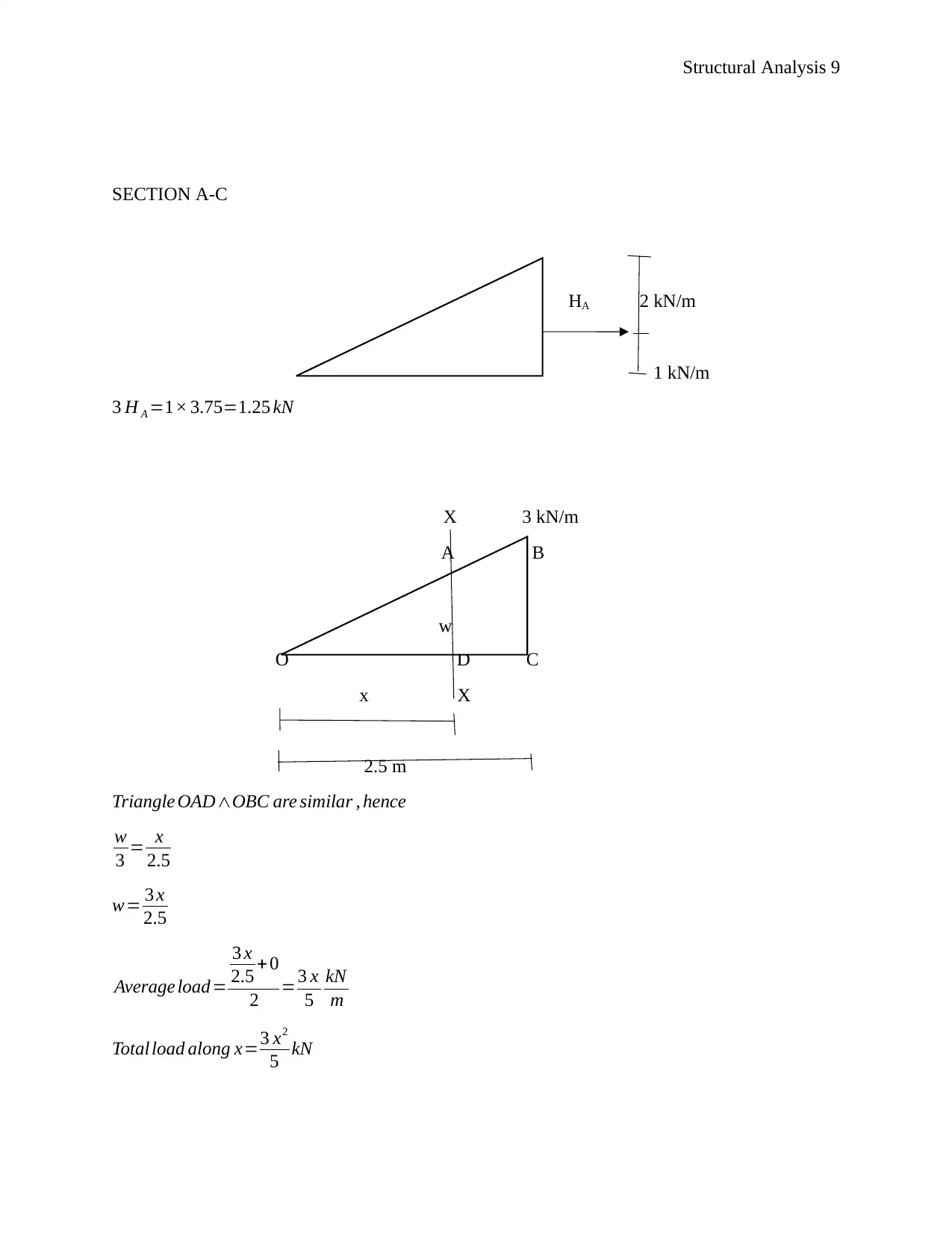
SECTION A-C
HA 2 kN/m
1 kN/m
3 H A =1× 3.75=1.25 kN
X 3 kN/m
A B
W
O D C
x X
2.5 m
Triangle OAD∧OBC are similar , hence
w
3 = x
2.5
w= 3 x
2.5
Average load=
3 x
2.5 + 0
2 =3 x
5
kN
m
Total load along x=3 x2
5 kN
w

Structural Analysis 10
Shear Force
Along the X−X line , SFxx=0.8−3 x2
5
At x=0
SF=0.8 kN
At x=2.5 m
SF=0.8− 3 ( 2.5 ) 2
5 =−2.95 kN
If SF =0
0.8−3 x2
5 =0 , x=1.15 m
Bending Moments
Along the X−X line , BM xx=0.8 x− 3 x2
5 ∙ x
3 =0.8 x− x3
5
At x=0
BM =0 kNm
At x=2.5 m
BM =0.8 ( 2.5 ) − ( 2.5 ) 3
5 =−1.125 kNm
Maximum BM occurs when SF=0. For our case , at x=1.15 m
BM =0.8 ( 1.15 )− ( 1.15 )3
5 =0.616 kNm
When BM =0 , then
0.8 x− x3
5 =0
0.8− x2
5 =0
x2
5 =0.8
x=2

Structural Analysis 11
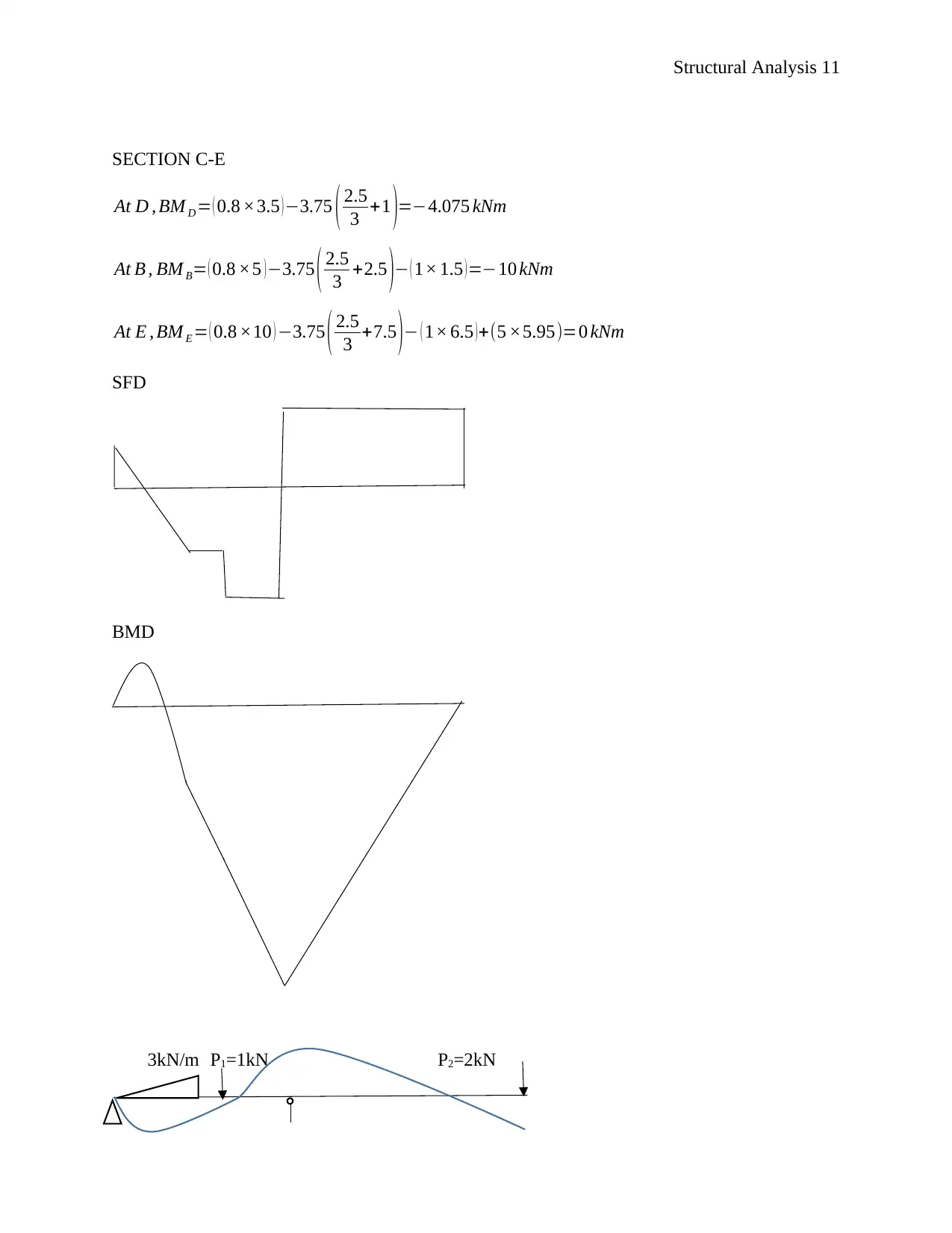
SECTION C-E
At D , BM D= ( 0.8 ×3.5 )−3.75 ( 2.5
3 +1 )=−4.075 kNm
At B , BM B= ( 0.8 ×5 )−3.75 ( 2.5
3 +2.5 )− ( 1× 1.5 )=−10 kNm
At E , BM E = ( 0.8 ×10 ) −3.75 ( 2.5
3 +7.5 )− ( 1× 6.5 )+(5 ×5.95)=0 kNm
SFD
BMD
3kN/m P1=1kN P2=2kN

Structural Analysis 12
References
Bansal, R. K., 2010. Srength of Materials. 4th ed. New Delhi: Laxmi Publications (P) Ltd..
Beer, F. P., Jonston Jr., E. R. & DeWolf, J. T., 2015. Mechanics of Materials. 7th ed. New York:
McGraw-Hill Education.
Gere, J. M. & Goodno, B. J., 2013. Mechanics of Materials. 8th ed. Stamford: Cengage
Learning.
Menon, D., 2008. Structural Analysis. 1st ed. Oxford: Alpha Science.